多重積分、二重積分について講義します。二重積分の計算：理論と例多重積分の解法

Def . レット・イット・ビー
,

.

このセットは、クローズドギャップまたはクローズドバーと呼ばれます。 .

セットはオープンギャップと呼ばれます

またはのオープンバー .

Def . 間隔の測定と数量は次のように呼ばれます。

（より正確に
).

Def . もしも
そのような
その後、間隔縮退と呼ばれ、
.

間隔測定プロパティ：

NS）。陽性：
、と
場合に限り -退化しています。

NS）。正の均一性：。

v）。加法性：

* にとって
そのような
;

* にとって
と

.

NS）。測定の単調性：。

Def . バーの直径（ギャップ）は次の値です。

ご了承ください
と
同じことではありません。たとえば、 -退化してから
、 NS
（一般的に言えば）。

ここで：*;

* ;*
.

Def . 骨材
サブスペース間隔の分割と呼ばれます、もしも： *;

*
; *
; *
; *
.

数量
パーティションパラメータと呼ばれます NS（ここで
).

Def . 分割パーティションの調整と呼ばれますパーティションのすべての要素の場合分割された要素を分割することによって得られます .

それが示されています：
..。読んだ：小さいまた大きい .

大きい方と小さい方の関係については、次のようになります。

*。推移性-; *。
;

*.

; *.

|
.

§。多重積分の定義

しよう
-ティンバー（ギャップ） ,
-ギャップを分割する私..。パーティションの各間隔でポイントをマークする
.

我々が得る
マークされたポイントで分割
.

数量
関数の積分リーマン和と呼ばれます NS (NS）間隔で私マークされたポイントで分割する
.

Def :
=
=
.

を示す -バーに統合可能な一連の関数私私たちは書き留めます：

Def : ε > 0 δ>0<.

関数の場合 NS(NS）オン私と分割
-で示す
-関数の最大値と最小値 NS(NS）オン私 kその後、量
=
と
=
ダルブーの下限と上限の合計と呼ばれます。

§. 多重積分の存在に関するダルブー基準.

NS 0 . 機能するには
バーに統合可能でした（それらの。
）が必要十分である

. Δ▲.

ユークリッド空間のバー上の関数の統合が決定されます。ユークリッド空間からの任意の有界集合に関数を統合する方法は？

関数の積分を定義しましょう NS セットで
.

Def : しよう
と
-制限付き、つまり
..。関数
セットの特性関数と呼ばれます NS.

それで：
≡
.

セット上の積分の定義は、どのバーを含むかに依存しません NS選択された、つまり

.

これは、集合に対する積分の定義が正しいことを意味します。

可積分性に必要な条件。機能するには NS(NS）オン NS可積分であるため、 NS(NS）に制限されていました NS. Δ▲.

§。多重積分の性質。

1  . 直線性：多く NS NSセットに統合可能な機能 NS -線形

スペース、そして
-線形汎関数。

2  . 正規化条件：
..。別の形式の表記
実際、ユークリッド空間から任意の集合の測度を決定します。

3  . ルベーグ測度ゼロのセットの積分が存在する場合、それは

はゼロです。

ノート：沢山の NSルベーグ測度ゼロのセットと呼ばれ、

もしも

そのような
と
.

4  . NS。;NS。;

v。もしも
と -ゼロから NS、それから

5  .
と NS=NS p.c. （ほとんどどこでも） NS、それから
.

6  . 加法性：もし
と
それから

一般に：
.

Δ。平等から続く：▲

7  . 単調：
と
それから
.

8  . 不等式の統合：if
伊藤

9  . しよう

..。に
、セットの内部ポイントがあることが必要十分です NS、ここで NS (NS）> 0であり、連続です。

10  . 統合される機能のモジュールの統合可能性：
.

11  . 平均定理：
,
オン NSサインを保存し、
、それから

セットの場合 NS-接続され、 NS(NS）継続的
それから
そのような
.

12  . 非負の関数の積分が0に等しくなるために

必要十分 NS(NS）= 0ほとんどどこでも NS.

13  . フビニの定理。二重積分の場合：

地域にしましょう
-長方形：。次に、内部の単一積分が存在する条件下で、二重積分を見つけるために、繰り返し積分に進むことができます（図Aを参照）。

、また

積分領域が長方形でない場合でも、フビニの定理は有効であり、次の形式になります（図bを参照）。

. (*)

ノート：統合の外部制限は定数である必要があります。統合の内部制限は、統合がまだ実行される変数に依存する場合があります。

式（*）は、セットの特性関数を使用して取得できます。 NS.

多重積分の場合：

ユークリッド空間のいくつかのサブセットをしましょうと ..。ユークリッド空間のサブセットである、これらのセットのデカルト積を定義します
:.

次に、フビニの定理
次のようになります：
.

定理はバーにも有効です NSと Y、およびより複雑な構成の場合。

例：

1 0 . 計算する
地域の境界なら
方程式によって与えられる：

..。領域の境界を定義する曲線の交点を見つけると、2つの点が得られます。

と

..。次に、反復積分に渡すときの積分の限界の可能な配置は次のようになります。

NS）。
;

0 . 再積分での積分の順序を変更します。

–

レシピ：二重積分で積分の限界を設定するときは、積分の外側の限界から始めることをお勧めします。

0 . 計算：

、もしも

反復積分に渡すと、次のようになります。
.

この場合、三重積分では、限界の配置は積分の内部限界から始めなければなりません。次に、エリアを投影します V飛行機の中 xOy

エリアに制限を設定する NS-飛行機に横たわっている xOy.

4 0 . 再積分での積分の順序を変更します。
.

多重積分に関するOstrogradskiiの研究についてもう少し詳しく見ていきましょう。

三重積分を二重積分に変換するためのオストログラードスキーの公式。これは通常、次の形式で記述します。

ここで、div AはベクトルAのフィールドの発散であり、

Anは、境界面の外側の法線nの単位ベクトルによるベクトルAの内積です。数学の文献では、以前はGaussとGreenの名前に関連付けられていました。

実際、回転楕円体の引力に関するガウスの研究では、たとえばP = x、Q = R = 0などの式（1）の非常に特殊なケースしか見ることができません。J.Greenについては、彼の研究で電気の理論についてであり、式（1）の磁性はまったくありません。それは、三重積分と二重積分の間の別の関係、すなわち、ラプラス演算子のグリーンの公式を導き出しました。これは、次の形式で記述できます。

もちろん、次のように設定することで、（2）から式（1）を導き出すことができます。

同じように、式（1）から式（2）を得ることができますが、グリーンはこれを行うことさえ考えていませんでした。

ここで、ボリューム上の積分は左側にあり、境界面上の積分は右側にあり、これらは外側の法線の方向余弦です。

オストログラードスキーのパリの写本は、完全な確信を持って、積分定理（1）の発見と最初の伝達の両方が彼のものであったことを証言しています。 1826年2月13日にパリ科学アカデミーに提出された「積分学の定理の証明」で行われているように、最初に表現され、証明されました。その後、「回想録」のその部分で再び定式化されました。内部の熱の伝播について固体オストログラードスキーが1827年8月6日に発表した」。「回想録」はフーリエとポアソンにレビューのために渡され、原稿の両方の部分の最初のページのエントリから明らかなように、後者は確かにそれを読んだ。もちろん、ポアソンは、弾性理論に関する彼の研究の発表の2年前に、オストログラードスキーの研究で出会った定理を自分自身に帰することさえ考えていませんでした。

オストログラードスキーとグリーンの多重積分に関する研究の関係については、「熱理論に関する注記」で、非常に特殊なケースとして、グリーン自身の公式を取り入れた公式が導き出されたことを思い出します。オストログラードスキーが「ノート」で使用した、今では珍しいコーシーの象徴は、最近までこの重要な発見を研究者から隠していました。もちろん、グリーンは、彼の名前を冠したラプラス演算子の公式の発見と1828年の最初の出版の名誉を保持しています。

三重積分を二重積分に変換するための式の発見は、Ostrogradskiiがn倍積分を変化させる問題を解決するのに役立ちました。つまり、発散のタイプの式の積分を変換するための一般式を導き出すのに役立ちました。 n次元領域上で、および方程式L（x、y、z、...）= 0を使用した境界超表面S上の積分。前の表記法に従うと、式は次の形式になります。

しかし、オストログラードスキーは、私たちが使用する幾何学的な画像や用語を使用していませんでした。多次元空間の幾何学は、当時まだ存在していませんでした。

多重積分の変分法に関する回想録では、そのような積分の理論に関するさらに2つの重要な質問が検討されています。まず、Ostrogradskiiは、多次元積分の変数変換の公式を推測します。第二に、彼は初めて、適切な制限内の各変数に対してn回の連続積分を使用してn回積分を計算する方法の完全で正確な説明を提供します。最後に、この回想録に含まれている式から、簡単に推測できます原則多次元積分のパラメータに関する微分。被積分関数だけでなく、積分領域の境界もこのパラメータに依存します。この規則は、後の数学者がこの回想録の公式の1つでそれを特定するほど自然な方法で、回想録に存在する公式に基づいています。

Ostrogradskiiは、多重積分の変数変換に特別な作業を捧げました。二重積分の場合、対応する規則は、オイラーによる形式変換を使用して導出され、三重積分の場合、ラグランジュによる変換を使用して導出されました。しかし、ラグランジュの結果は正しいものの、彼の推論は正確ではありませんでした。彼は、新旧の変数（座標）のボリューム要素が互いに等しいという事実から進んでいるように見えました。 Ostrogradskiiは、変数を変更するためのルールの前述の導出で同様の間違いを犯しました。記事「多重積分での変数変換について」で、Ostrogradskiyはラグランジュ誤差を開示し、また、二重積分で変数を変換するための明確な幾何学的方法を初めて概説しました。マニュアルにも記載されています。つまり、式に従って積分の変数を変更すると、積分の領域は2つのシステムu = const、v = constの座標線によって微小な曲線の四角形に分割されます。次に、最初に無限に狭い曲線ストリップに対応する要素の要素を合計し、次に要素がすべてなくなるまでストリップごとに要素を合計し続けることで、積分を取得できます。簡単な計算で面積が得られます。これは、小さな高次までの平行四辺形と見なすことができます。ここで、式は、面積が正になるように選択されます。その結果、よく知られている式が得られます

次のように定義された2つの変数の関数の場合 z = NS(NS, y) .

二重積分は次のように記述されます。

ここ NS-線で囲まれた平面図形。その式（等式）は、二重積分を計算するタスクで与えられます。左と右-左側の変数が等しい NS、および上下-左側の変数が y..。この場所とさらに-二重積分を計算する手法を理解するための最も重要なものの1つ。

二重積分を計算する -言及された図の面積に等しい数を見つけることを意味します NS .

触れるまで 二重積分の定義 、しかし私たちはそれを計算することを学びます。いくつかの問題を解いて計算すると、二重積分とは何かを理解しやすくなるため、このレッスンの最後に二重積分の定義があります。少し先に進むと、二重積分の定義も前述の図に関連していることに注意できます。 NS .

フィギュアなら NSは長方形であり、それを囲むすべての線は直線です。フィギュアなら NS-は曲線であり、左側と右側は直線で囲まれ、上下は-割り当てで指定された等式によって与えられる曲線で囲まれます。フィギュアが NS-三角形ですが、そのような場合についてはもう少し先です。

したがって、二重積分を計算するには、図の境界線を並べ替える必要があります。 NS、厳密な名前があります-統合の領域。左右と上下に並べ替えます。これは次の場合に必要になります 二重積分を反復積分に還元する -二重積分を計算する方法。

長方形エリアの場合：

湾曲した領域の場合：

そして、これはすでに私たちに馴染みのある特定の積分の解であり、積分の上限と下限が与えられています。形状の境界線を定義する式 NSは、すでに近づいている通常の定積分の積分の限界になります。

二重積分の反復積分への縮小

長方形エリアケース

そのような関数に二重積分を持たせましょう

に この二重積分を計算する 、それを繰り返し積分に減らす必要があります。

最初に内側（右）の定積分を計算する必要があり、次に-外側（左）の定積分を計算する必要があります。

あなたは役割を変えることができます NSと y

例1。二重積分を計算する

yが定数であると仮定して、内側（右）の積分を計算します。受け取ります。

例2。二重積分を計算する

解決。この二重積分を反復積分に減らします

図面では、統合の領域を構築します：

ここで、計算したばかりの内側（右）積分の外側（左）積分を計算します。

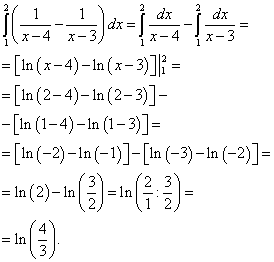
結果は、この二重積分の解になります。

自分で二重積分を計算し、解を確認します

湾曲した領域または三角形の領域の場合

再び2つの変数の関数を与えましょう NS(NS, y) 、およびの制限 NS：すでに少し異なる種類：

このエントリは、図が NS直線領域の場合のように、左右の境界-直線 NS = NSと NS = NS、ただし、上下は方程式とで与えられる曲線です。言い換えれば、とは関数です。

そのような関数にも二重積分を持たせましょう

この二重積分を計算するには、次の形式の反復積分に減らす必要があります。

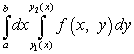ここに統合の限界 NSと NSは数値、およびは関数です。三角形の領域の場合、関数の1つまたはは直線の方程式です。このような場合は、例3で分析します。

直線領域の場合と同様に、最初に右の定積分を計算し、次に左の定積分を計算する必要があります。

同様に、役割を交換できます NSと y..。次に、反復積分は次の形式になります

このような繰り返し積分は、同じ方法で解く必要があります。最初に内側（右）積分、次に外側（左）積分です。

例5。二重積分を計算する

解決。この二重積分を反復積分に減らします

図面では、統合領域を作成し、それが三角形であることを確認します。

xを定数として、内側（右）の積分を計算します。受け取ります。

ここで、計算したばかりの内側（右）積分の外側（左）積分を計算します。まず、この積分を積分の合計として表します。

最初の項を計算します。

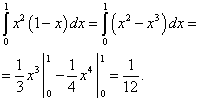
2番目の項を計算します。

3番目の項を計算します。

合計を取得します。これは、この二重積分の解になります。

例6。二重積分を計算する

解決。この二重積分を反復積分に減らします

図面では、統合の領域を構築します：

xを定数として、内側（右）の積分を計算します。受け取ります。

ここで、計算したばかりの内側（右）積分の外側（左）積分を計算します。

結果は、この二重積分の解になります。

NS-正解と不正解、 y-統合の正しいドメインと正しくないドメイン

二重積分の積分領域は、積分領域を部分に分割し、対応する各反復積分を個別に解く必要があるような線によって制限されることがあります。これらは次の場合です。

1）統合の領域は、下または上（左または右）の境界の形で2つ以上の直線または曲線を持っている図です;

2）積分領域は図形であり、その境界線は3点以上で交差します。

上記が統合領域の左または右の境界に適用される場合、つまり、次の式で表される線によって設定される制約 NS、その後、統合の領域は呼び出されます NS-間違い。ストレートの場合 y = y0 対応する境界と1点でのみ交差し、1つの直線または曲線のみが境界として機能する場合、積分領域はと呼ばれます。 NS- 正しい

同様に、線で定義された境界線が y、真っ直ぐ NS = NS0 複数の点で交差する場合、または複数の直線または曲線が境界として機能する場合、統合領域はと呼ばれます。 y-間違い。今すぐ標識を表示する y-おそらく、正しい領域は非常に単純です。

これまでのところ、 NS-正しくなく、 y-統合の正しい領域。次に、正当性条件に違反した場合を考えてみましょう。

例7。線で囲まれたの積分領域である二重積分を計算します y = NS , xy = 1 , y = 2 .

解決。統合の分野は y-間違っています。下限を1行で設定できないためです。 y = y(NS) ..。上の写真でわかるように、下の境界線はで構成されています y = NS（ダークバーガンディ）と xy= 1（緑）。したがって、直接 NS= 1（黒）積分領域を2つの部分に分割できます-と。

この二重積分は次のように計算されます。

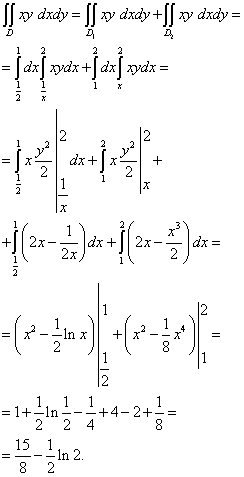
統合の順序を変更する

上記のように、二重積分を反復積分に減らした後、変数を変更できます NSと y役割、つまり、統合の順序を変更します。

統合の順序の変化は、次の単語で比喩的に説明できます。「ヘンリー」について：これは、ジャングルの住人がどのように振る舞うかです。疑念のジャングル。」そして同じ：「Chalmersは手紙を千の最小の断片に引き裂き、彼の高価なカーペットを引き裂き始め、それを前後に歩調を合わせた。」（（ O.ヘンリー. マディソンスクエアのシェヘラザード.)

次に、変数に関して左積分がある場合 NS、そして正しいもの-によって y、統合の順序を変更した後、すべてが逆になります。次に、「新しい」ゲームの統合の制限を「古い」xから「借用」し、「新しい」xの統合の制限を次の形式で取得する必要があります。 逆関数、ゲームの限界を設定するxの方程式を解きました。

例8。

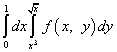解決。積分の順序を変更すると、ゲーム全体の積分は左になり、xの積分は右になります。「新しい」ゲームの統合の制限は、「古い」xから借用されます。つまり、下限はゼロに等しく、上限は1に等しくなります。「古い」ゲームの積分の限界は、方程式とで与えられます。 xについてこれらの方程式を解くと、xの積分の新しい限界が得られます。

（下）と（上）。

したがって、積分の順序を変更した後、繰り返される積分は次のように記述されます。

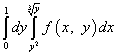二重積分の積分の順序を変更した後、積分領域はしばしば次のようになります。 y-間違っているまたは NS-正しくありません（前の段落を参照）。次に、積分領域を部分に分割し、対応する各反復積分を個別に解く必要があります。

統合領域を部分に分割することは多くの学生にとって一定の困難を伴うため、前の段落で示した例に限定するのではなく、さらにいくつかの例を検討します。

例9。再積分のために積分の順序を変更する

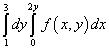解決。したがって、この反復積分の積分領域は直線で囲まれています y = 1 , y = 3 , NS = 0 , NS = 2y .

異なる順序で統合する場合、領域の下限は2本の直線で構成されます。 ABと 紀元前方程式によって与えられます y= 1および y = NS/ 2、これは下の図で見ることができます。

この不確実性から抜け出す方法は、統合領域を2つの部分に分割することです。統合領域は直線で分割されます BM..。逆関数を見つけることにより、積分の新しい限界を計算します。このソリューションによると、積分の順序を変更した後の反復積分は、2つの積分の合計に等しくなります。

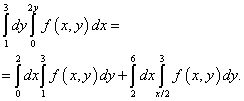
当然、同じことが二重積分の解にもなります。これは、この例の条件で与えられた反復積分になります。

例10。再積分のために積分の順序を変更する

解決。したがって、反復積分の積分領域は直線で囲まれます。 NS = 0 , NS= 2および曲線と。

下の写真に見られるように、軸に平行な直線 0xは、2点以上で積分領域の下限を超えます。

したがって、図では黒で描かれている直線によって、統合領域を3つの部分に分割します。逆関数を見つけることにより、積分の新しい限界を計算します。 3つの新しい統合領域の制限は次のとおりです。

この解決策によれば、積分の順序を変更した後の反復積分は、3つの積分の合計に等しくなります。

3つの積分の同じ合計は、二重積分に等しくなります。これは、この例の条件で与えられた反復積分になります。

それでも、不可抗力の状況は、前のステップですでに学生に干渉することがよくあります-統合の限界を設定します。不安と混乱には何らかの理由がないわけではありません。通常、積分領域を部分に分割し、繰り返される積分（積分の表）を解くのに図面を見るだけで十分な場合は、積分限界を設定するためのトレーニング経験が必要です。。統合の制限の配置のみに焦点を当て、ほぼ自動的にドメインのパーティションに焦点を当て、ソリューション自体を省略した例を実行してみましょう。

例11。積分の領域があれば、二重積分の積分の限界を見つける NSは次のように設定されます。

y - 2NS ≤ 0;
2年 - NS ≥ 0;
xy ≤ 2.

解決。明示的に（ NSと y「不純物なし」）、積分領域の境界線は指定されていません。 xの場合、ほとんどの場合、ゲームを通じて表現された上下の境界に一点で接する直線であることが判明するため、このパスに正確に沿って進みます。さらに、統合の順序を変更すると、同じ領域の統合領域が得られます。ゲームに関する不等式を解決して、次のことを取得しましょう。

y ≤ 2NS;
y ≥ NS/2;
y ≤ 2/NS.

結果の線を図面に作成します。 x積分の限界は確かに線です NS= 0および NS= 2。しかし、統合の領域は y-間違っています。上部の境界線を1行で設定できないためです。 y = y(NS) .

Depositfilesからダウンロード

講義5-6

トピック2。多重積分。

二重積分。

質問を管理します。

1.二重積分、その幾何学的および物理的意味

2.二重積分の性質。

3.デカルト座標での二重積分の計算。

4.二重積分の変数変換。極座標での二重積分の計算。

関数をしましょう z = NS (NS , y）は、有界の閉じた領域で定義されます NS飛行機。エリアを分割しましょう NS任意に NSエレメンタリークローズドリージョン  1 , … , NSエリア付き  1 , …,   NSと直径 NS 1 , …, NS NS それぞれ。私たちは NS領域の直径の最大  1 , … ,  NS..。すべての地域で  k任意の点を選択してください NS k (NS k 、y k）そして作曲する 積分和関数 NS(x、y)

NS =
(1)

意味。 二重積分関数 NS(x、y）地域別 NS積分和の限界と呼ばれます

, (2)

存在する場合。

コメント。積分和 NS領域がどのように分割されているかによって異なります NSとポイントの選択 NS k (k=1, …, NS）。ただし、制限
、存在する場合、領域を分割する方法に依存しません NSとポイントの選択 NS k .

二重積分が存在するための十分な条件。関数が次の場合、二重積分（1）が存在します NS(x、y) 連続 NS有限数の区分的に滑らかな曲線を除いて、 NS..。以下では、検討中のすべての二重積分が存在すると仮定します。

二重積分の幾何平均。

もしも NS(x、y) エリア内で≥0 NSの場合、二重積分（1）は、図に示されている「円筒形」の物体の体積に等しくなります。

V =
(3)

円筒形のボディは、下から領域で囲まれています NS、上から表面の一部 z = NS (NS , y）、側面からこのサーフェスと領域の境界を結ぶ垂直線分 NS。

二重積分の物理的意味。平板質量。

平板を与えましょう NS既知の密度関数γ（ NS、で）、次にプレートDをパーツDに分割します私任意のポイントを選択します
、プレート質量について取得します
、または、式（2）と比較して：

(4)

4.二重積分のいくつかの特性。

直線性。もしもと数値定数である場合

加法性。エリアの場合 NS エリアに「分割」 NS 1 と NS 2、次に

3）限られたエリアのエリア NSに等しい

(5)

デカルト座標での二重積分の計算。

地域を与えましょう

写真1

D = { (NS , y ): a≤x≤b , φ 1 (NS ) ≤y≤φ 2 (NS ) } (6)

領域 NS 直線の間のストリップで囲まれています NS = NS , y = NS、下からと上からは、それぞれ曲線で囲まれています y = φ 1 (NS ) と y = φ 2 (NS ) .

領域全体の二重積分（1） NS（4）は、反復積分に渡すことによって計算されます。

(7)

この反復積分は次のように計算されます。まず、内部積分が計算されます

変数による y、ここで NS一定と見なされます。結果は変数の関数です NS、次に、変数に関するこの関数の「外部」積分が計算されます。 NS .

コメント。式（7）に従って反復積分に渡すプロセスは、二重積分の積分限界の配置と呼ばれることがよくあります。統合の制限を設定するときは、2つの点に注意する必要があります。第一に、積分の下限は上限を超えてはなりません。第二に、外部積分の限界は一定でなければならず、内部積分は一般に外部積分の積分の変数に依存する必要があります。

今、地域をしましょう NS形があります

D = { (NS , y ) : c≤y≤d , ψ 1 (y ) ≤x≤ψ 2 (y ) } . (8)

それで

. (9)

その地域が NS（6）と（8）の形で同時に表すことができます。次に平等

(10)

ある反復積分から別の等式（10）への通過は次のように呼ばれます。 統合の順序を変更する二重積分で。

例。

1）積分の積分の順序を変更します

解決。反復積分の形から、領域を見つけます

D = { (NS , y ): 0 ≤x≤ 1, 2 x≤y≤ 2 } .

エリアを描きましょう NS..。図から、この領域は直線の間の水平ストリップに位置していることがわかります y =0, y= 2および行間 NS =0 と NS= D

計算を簡素化するために変数が変更されることがあります。

,
(11)

関数（11）が連続的に微分可能であり、行列式（ヤコビアン）が考慮される定義域で非ゼロである場合：

(12)

ロシア連邦教育科学省

コースワーク

規律：高等数学

（基本的な線形計画法）

トピックについて：多重積分

完了：______________

教師：___________

日にち ___________________

学年 _________________

サイン ________________

ヴォロネジ2008

1多重積分

1.1二重積分

1.2三重積分

1.3曲線座標の多重積分

1.4多重積分の幾何学的および物理的応用

2曲線積分と面積分

2.1曲線積分

2.2面積分

2.3幾何学的および物理的アプリケーション

参考文献

1多重積分

1.1 二重積分

オキシ平面で、線Lで囲まれた閉じた領域Dを考えます。この領域をいくつかの線でn個の部分に分割します。

、およびこれらの各部分のポイント間の対応する最大距離は、d 1、d 2、...、dnで表されます。各パートでポイントРiを選びましょう。

関数z = f（x、y）が定義域Dで与えられるとします。選択した点でのこの関数の値をf（P 1）、f（P 2）、…、f（P n）で表し、f（P i）ΔSiの形式の積の合計を構成します。：

, (1)

定義域Dの関数f（x、y）の積分和と呼ばれます。

積分和（1）の同じ制限が存在する場合

そして、それは定義域Dを部分に分割する方法にも、それらの中の点P iの選択にも依存しないので、定義域Dに対する関数f（x、y）の二重積分と呼ばれます。が示されています

. (2)

線で囲まれた領域Dの二重積分の計算

x = a、x = b（a< b), где φ 1 (х) и φ 2 (х) непрерывны на (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла: