I. Definicija, osnovne lastnosti in grafi hiperboličnih funkcij. Hiperbolične funkcije Th matematična funkcija
11 Osnovne funkcije kompleksne spremenljivke
Spomnimo se na definicijo kompleksnega eksponenta -. Potem
Razširitev Maclaurinove serije. Polmer konvergence te serije je + ∞, kar pomeni, da je kompleksni eksponent analitičen na celotni kompleksni ravnini in
(exp z) "= exp z; exp 0 = 1. (2)
Prva enakost tukaj izhaja na primer iz diferenciacijskega izreka po členu za potenzivni niz.
11.1 Trigonometrične in hiperbolične funkcije
Sinusna kompleksna spremenljivka imenovana funkcija

Kosinus kompleksne spremenljivke obstaja funkcija

Hiperbolični sinus kompleksne spremenljivke definiran takole:
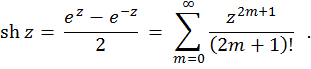
Hiperbolični kosinus kompleksne spremenljivke je funkcija

Omenimo nekaj lastnosti na novo uvedenih funkcij.
A.Če je x∈ ℝ, potem cos x, sin x, ch x, sh x∈ ℝ.
B. Obstaja naslednja povezava med trigonometričnimi in hiperboličnimi funkcijami:
cos iz = ch z; sin iz = ish z, ch iz = cos z; sh iz = isin z.
B. Osnovne trigonometrične in hiperbolične identitete:
cos 2 z + sin 2 z = 1; ch 2 z-sh 2 z = 1.
Dokaz glavne hiperbolične identitete.
Glavna trigonometrična identiteta izhaja iz glavne hiperbolične identitete ob upoštevanju povezave med trigonometričnimi in hiperboličnimi funkcijami (glej lastnost B)
G Formule za seštevanje:
Še posebej,
D. Za izračun izvodov trigonometričnih in hiperboličnih funkcij je treba uporabiti izrek o diferenciaciji potekovnega niza po členu. Dobimo:
(cos z) "= - sin z; (sin z)" = cos z; (ch z) "= sh z; (sh z)" = ch z.
E. Funkcije cos z, ch z so sode, funkcije sin z, sh z pa lihe.
G. (periodičnost) Funkcija e z je periodična s periodo 2π i. Funkcije cos z, sin z so periodične s periodo 2π, funkcije ch z, sh z pa periodične s periodo 2πi. Poleg tega
Če uporabimo formule vsote, dobimo
Z. Dekompozicije na resnične in namišljene dele:
Če enovrednostna analitična funkcija f (z) bijektivno preslika domeno D na domeno G, potem D imenujemo domena schlichtness.
IN. Domena D k = (x + iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
Dokaz. Iz relacije (5) sledi, da je preslikava exp: D k → ℂ injektivna. Naj bo w poljubno kompleksno število, ki ni nič. Nato rešimo enačbe e x = | w | in e iy = w / | w | z realnimi spremenljivkama x in y (izberi y iz polovičnega intervala)