I. Definizione, proprietà di base e grafici delle funzioni iperboliche. Funzioni iperboliche Th funzione matematica
11 Funzioni di base di una variabile complessa
Ricordiamo la definizione dell'esponente complesso -. Quindi
Espansione in serie di Maclaurin. Il raggio di convergenza di questa serie è + , il che significa che l'esponente complesso è analitico su tutto il piano complesso e
(exp z) "= espr z; esp 0 = 1. (2)
La prima uguaglianza qui segue, per esempio, dal teorema di differenziazione termine per termine per una serie di potenze.
11.1 Funzioni trigonometriche e iperboliche
Seno variabile complessa chiamata la funzione

Coseno di una variabile complessa c'è una funzione

Seno iperbolico di una variabile complessa definito così:
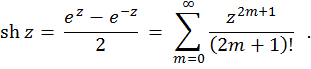
Coseno iperbolico di una variabile complessaè una funzione

Notiamo alcune proprietà delle funzioni appena introdotte.
UN. Se x∈ ℝ, allora cos x, sin x, ch x, sh x∈ ℝ.
B. Esiste la seguente connessione tra funzioni trigonometriche e iperboliche:
cos iz = ch z; sin iz = ish z, ch iz = cos z; sh iz = isin z.
B. Identità trigonometriche e iperboliche di base:
cos 2 z + sin 2 z = 1; cat 2 z-sh 2 z = 1.
Dimostrazione dell'identità iperbolica principale.
L'identità trigonometrica principale deriva dall'identità iperbolica principale quando si tiene conto della connessione tra funzioni trigonometriche e iperboliche (vedi proprietà B)
G Formule di addizione:
In particolare,
D. Per calcolare le derivate delle funzioni trigonometriche e iperboliche, si dovrebbe applicare il teorema sulla differenziazione termine per termine di una serie di potenze. Noi abbiamo:
(cos z) "= - sin z; (sin z)" = cos z; (ch z) "= sh z; (sh z)" = ch z.
e. Le funzioni cos z, ch z sono pari e le funzioni sin z, sh z sono dispari.
G. (Periodicità) La funzione e z è periodica con un periodo di 2π i. Le funzioni cos z, sin z sono periodiche con periodo 2π e le funzioni ch z, sh z sono periodiche con periodo 2πi. Inoltre,
Applicando le formule di somma, si ottiene
Z. Scomposizioni in parti reali e immaginarie:
Se una funzione analitica a valore singolo f (z) mappa biiettivamente un dominio D su un dominio G, allora D è chiamato dominio di schlichtness.
E. Dominio D k = (x + iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
Prova. Dalla relazione (5) segue che la mappatura exp: D k → ℂ è iniettiva. Sia w un qualsiasi numero complesso diverso da zero. Quindi, risolvendo le equazioni e x = | w | ed e iy = w / | w | con variabili reali x e y (scegli y da un semiintervallo)