Proučavanje oscilacija navojnog njihala i mjerenje. Laboratorijski rad iz fizike "proučavanje zakona matematičkog njihala"
Proučavanje zakona matematičkog njihala
Svrha rada: Proučite zakone matematičkog njihala i odredite ubrzanje gravitacije
Oprema: Klatno (kuglica na ovjesu), ravnalo, štoperica ili sat iz druge ruke.
Kratka teorija:
Matematičko njihalo je oscilator, koji je mehanički sustav koji se sastoji od materijalne točke smještene na bestežinskoj nerastegljivoj niti ili na bestežinskoj šipki u jednoličnom polju gravitacijskih sila.
Duljina njihala l udaljenost je od točke vješanja do težišta lopte.
Za praktični izračun razdoblja oscilacija upotrijebite formulu:
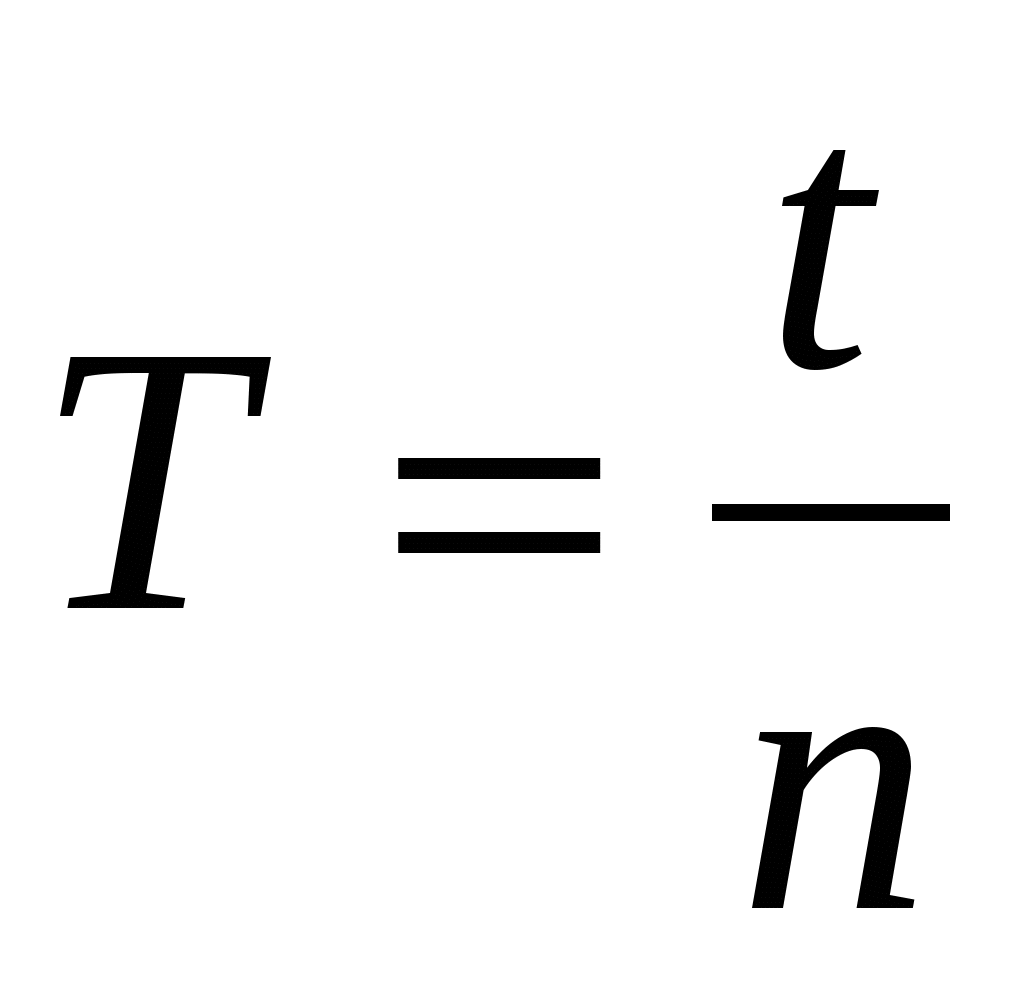 ,
,
gdje je T oscilacijsko razdoblje,
t je vrijeme osciliranja,
n je broj potpunih vibracija.
Prema zakonima titranja, razdoblje njihala može se odrediti formulom:
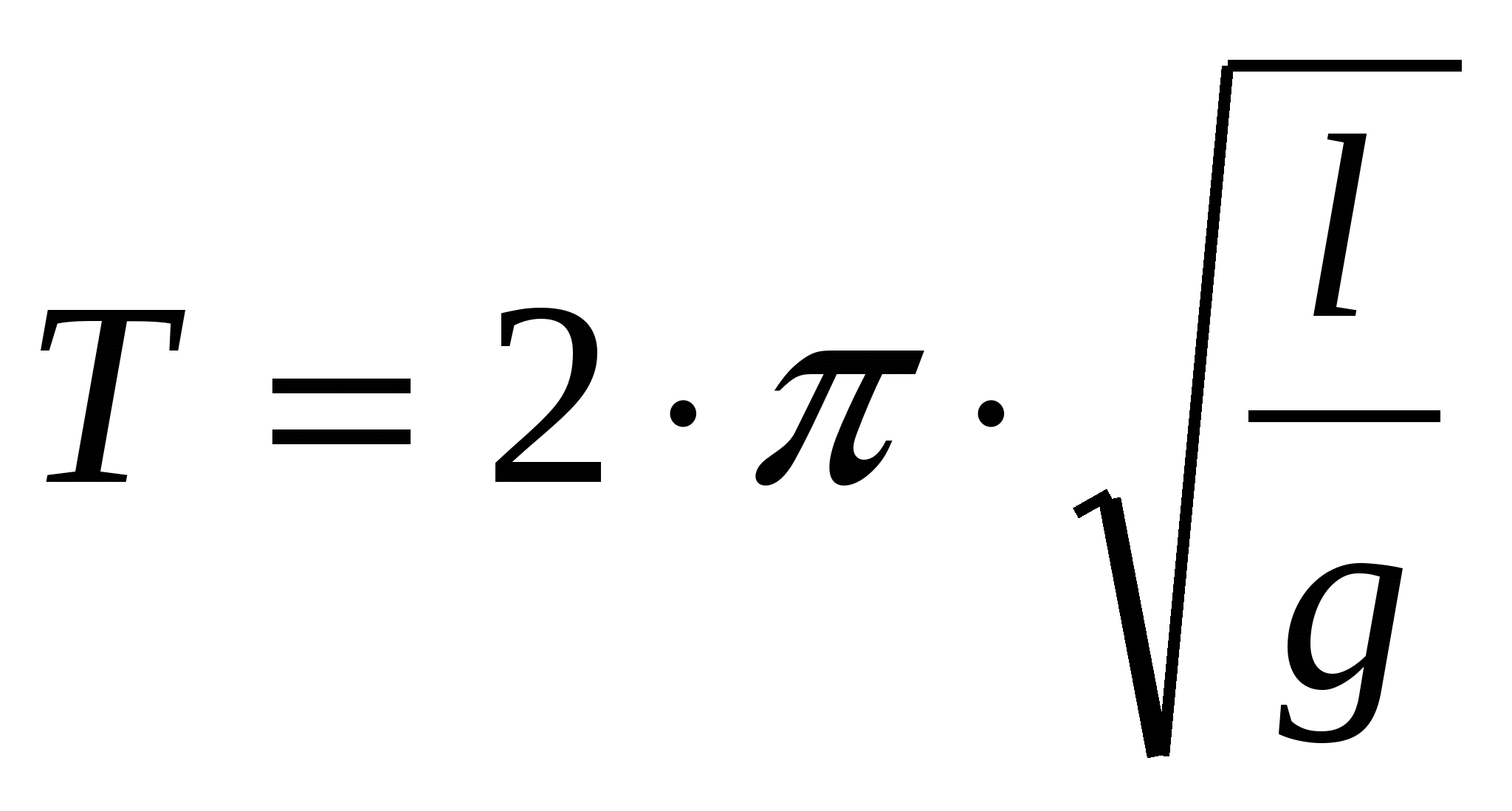 ,
,
Razdoblje titranja matematičkog njihala ne ovisi o masi kuglice.
Str  razdoblje titranja matematičkog njihala izravno je proporcionalno duljini njihala i obrnuto proporcionalno ubrzanju gravitacije. Ova se jednadžba naziva Huygensova formula.
razdoblje titranja matematičkog njihala izravno je proporcionalno duljini njihala i obrnuto proporcionalno ubrzanju gravitacije. Ova se jednadžba naziva Huygensova formula.
Povijest
Christian Huygens van Zuilichem (14. travnja 1629. - 8. srpnja 1695.). Nizozemski fizičar, matematičar, mehaničar i astronom i izumitelj. Rođen u Haagu. Studirao je pravo na Sveučilištu Leiden, ali nije prestao studirati matematiku. Na temelju Galileovih istraživanja riješio je niz problema u mehanici. 1656. godine, u dobi od 27 godina, dizajnirao je prvi sat s klatnom za eskaliranje. Stvaranje sata koji je mjerio vrijeme s dosad neviđenom točnošću imao je dalekosežne posljedice za razvoj fizičkog eksperimenta i ljudske praktične aktivnosti. Prije toga, uostalom, vrijeme se mjerilo odljevom vode, izgaranjem baklje ili svijeće. Teorija oscilacija koju je stvorio Huygens do 1673. bila je jedna od osnova za kasnije razumijevanje prirode svjetlosti.
Iz Huygensove formule, matematičkim transformacijama dobivamo izraz za ubrzanje gravitacije:
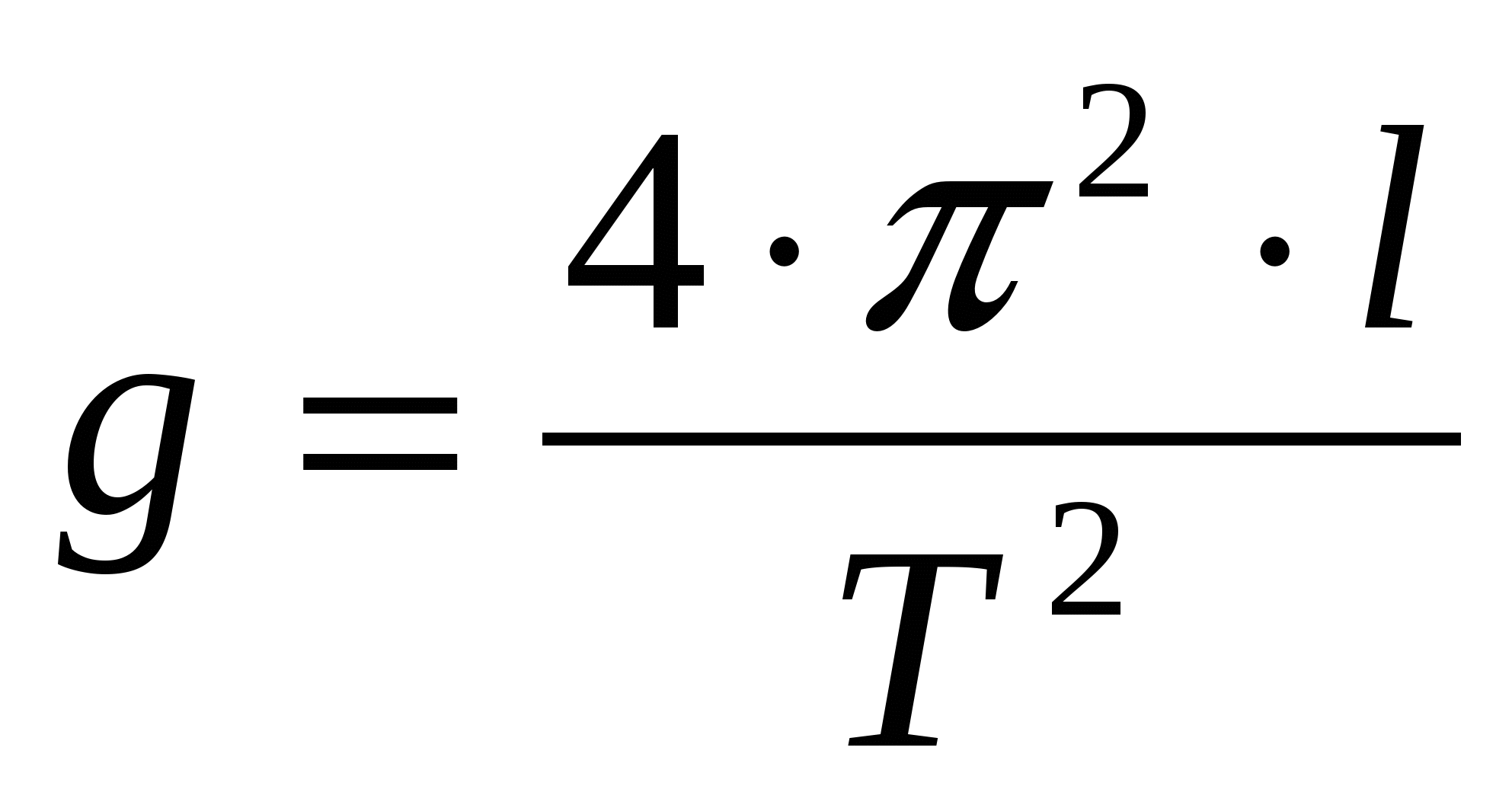

Stvarni model matematičkog njihala u našim eksperimentima bit će mala kuglica ovješena na tankoj elastičnoj niti. Veličina kuglice trebala bi biti mala u usporedbi s duljinom niti. To omogućuje pretpostavku da je sva masa koncentrirana u jednoj točki, u težištu kugle.
Napredak:
Odredite cijenu podjele uređaja:
vladar ...... ..m / div.
štoperica …… .s / div.
2. Odredite pogrešku instrumenata (apsolutna pogreška instrumenata jednaka je interval intervalu skale):
vladar Δ l = …… ..m
štoperica Δ t \u003d …… .s
Postavite maksimalnu duljinu viska i izmjerite ga l 1 \u003d… .m.
Pokrenite njihalo (kut otklona 10-15 0) i za vrijeme t prebrojite broj vibracija n (najmanje 7).
Promjenom broja vibracija ponovite pokus još 3 puta.
t 2 \u003d ………, n 2 \u003d …………. T 2 \u003d ………,
t 3 \u003d ………, n 3 \u003d …………. T 3 \u003d ………,
t 4 \u003d ………, n 4 \u003d …………. T 4 \u003d ………,
Promijenite duljinu njihala l 2 \u003d… .m i ponovite sva mjerenja.
Unesite podatke u tablicu.
№ mjerenja
Duljina njihala
l, m
№ iskustvo
Vrijeme osciliranja,
t, s
Broj vibracija
n
Razdoblje oscilacija,
T, s
Prosječna vrijednost razdoblja, T av, s
Ubrzanje slobodnog pada, g, m / s 2.
Podlo
ubrzanje slobodnog pada, g prosjek, m / s 2.
l usp \u003d
t Sri \u003d
relativno: apsolutno:
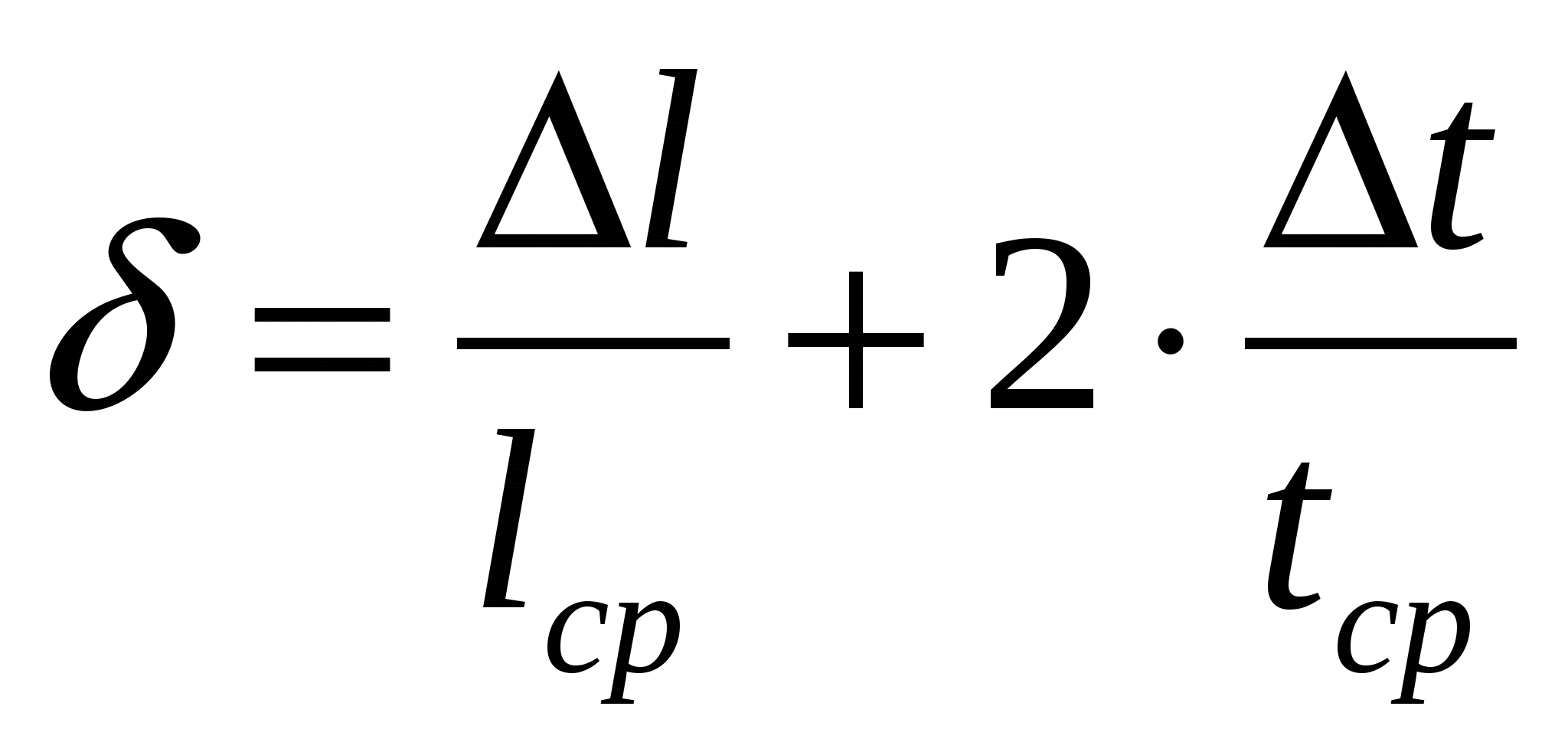
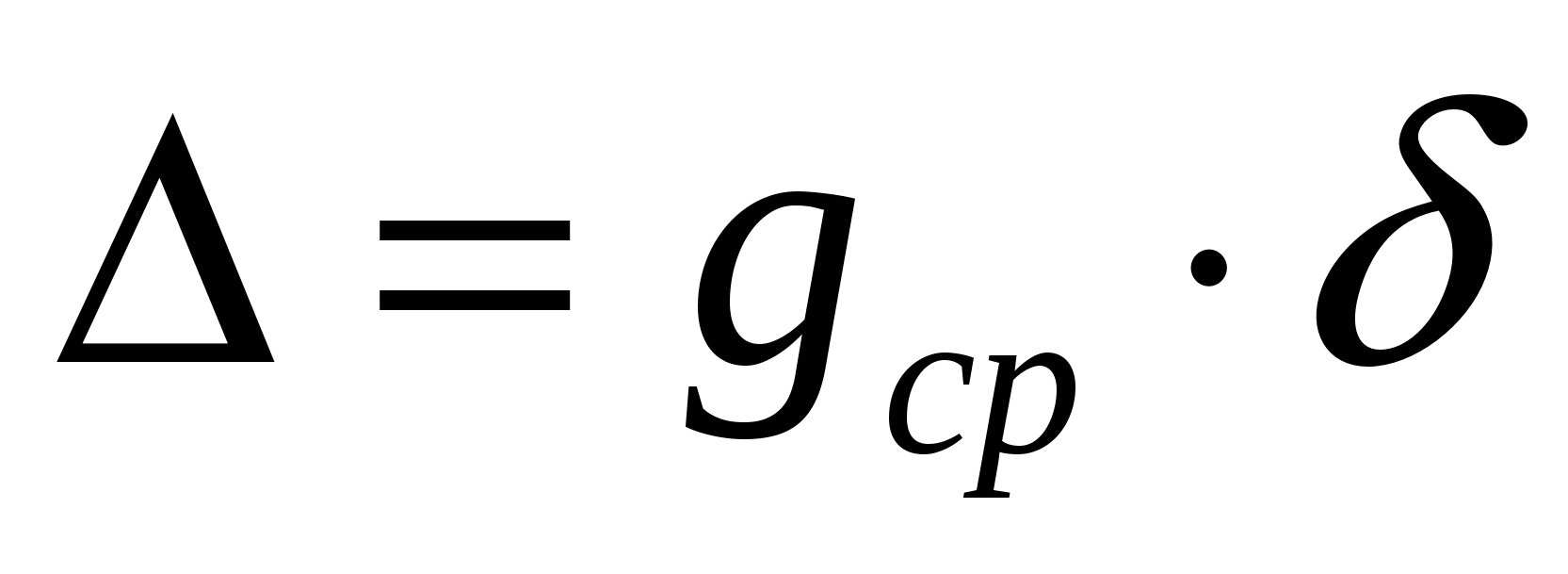 ,
,
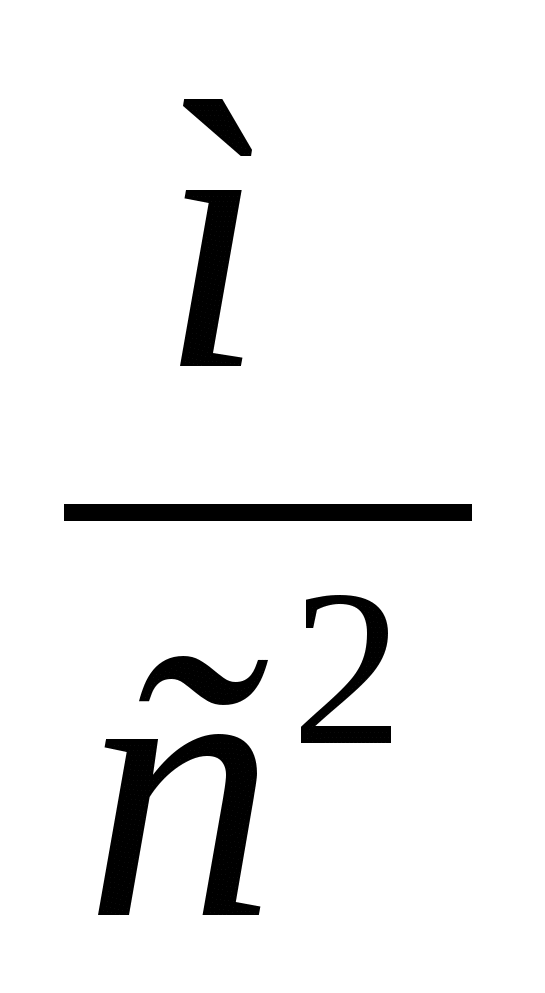
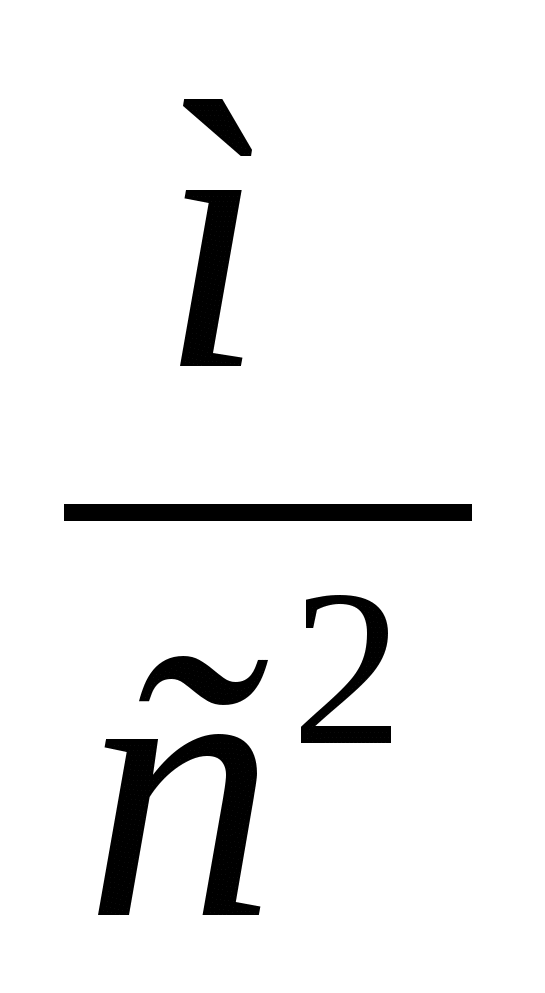
Test pitanja:
Koliko je dugo matematičko njihalo s razdobljem od 2 s?
Nađite masu utega koji na opruzi krutosti 250 N / m stvara 20 vibracija u 16 s.
Ubrzanje gravitacije na Mjesecu je 1,7 m / s 2. Koliki će biti period osciliranja matematičkog njihala na Mjesecu, ako je na Zemlji jednako 1 s? Ovisi li odgovor o težini tereta?
Koordinata oscilirajućeg tijela mijenja se prema zakonu x \u003d 0,5sin 45πt. Kolika je amplituda i period oscilacija?
Amplituda kontinuiranih oscilacija točke iznosi 12 cm, linearna frekvencija je 14 Hz, početna faza oscilacija je 0. Napišite jednadžbu gibanja točke x \u003d x (t).
Podjela ljestvice
Razlika (bez znaka) između vrijednosti fizička veličinašto odgovara oznakama skale koje ograničavaju podjelu. U digitalnim uređajima korak diskretnosti služi kao karakteristika koja zamjenjuje vrijednost podjele skale.
a) na ljestvici odaberite dva najbliža digitalizirana poteza;
c) razlika u vrijednostima (oduzmi manje od većih) za odabrane poteze podijelite s brojem dijeljenja.
H  ova slika prikazuje vagu termometra u velikoj mjeri. Koristit ćemo ga za ilustraciju pravila za izračunavanje cijene podjele.
ova slika prikazuje vagu termometra u velikoj mjeri. Koristit ćemo ga za ilustraciju pravila za izračunavanje cijene podjele.
a) odaberite digitalizirane poteze 20 ° C i 40 ° C.
b) 10 podjela (praznina) između njih
c) izračunajte: (40 ° C - 20 ° C): 10 podjela \u003d 2 ° S / div.
Odgovor: cijena podjela \u003d 2 ° S / div,
Digitalni uređaji nemaju eksplicitnu ljestvicu, a umjesto cijene podjele na njima je naznačena cijena jedinice najmanje značajne znamenke broja u očitanju uređaja.
Str 
primjer:
1) cijena podjele skale ovog uređaja iznosi 1 (konvencionalne jedinice) / div.
2
) cijena podjele skale ovog uređaja je 0,01 (konvencionalne jedinice) / div.
3
) podjela ljestvice ovog uređaja je 0,1 (konvencionalne jedinice) / div.
4) cijena podjele skale ovog uređaja je 0,001 (konvencionalne jedinice) / div.

Ja svrha rada
Promatranja oscilacijskih kretanja matematičkog njihala, provedena na uređaju čiji je funkcionalni dijagram prikazan na slici 1.
Mjerenje razdoblja oscilacija njihala pri različitim duljinama i amplitudama.
Određivanje izohronog načina oscilacija matematičkog njihala.
Proračun gravitacijskog ubrzanja lopte iz rezultata navedenih mjerenja.
II ... Teorijski dio
Razmotrimo uređaj koji se sastoji od male kuglice pričvršćene na fiksnu točku ovjesa pomoću neteživog navoja određene težine (slika 1).
Ako je veličina kuglice mnogo manja od duljinel niti, tada se lopta može vidjeti kao materijalna točka; a ako je masa kuglice mnogo veća od mase niti, tada se potonja može smatrati bestežinskom. Konac se također može smatrati nerastegljivim, pod uvjetom da gravitacija kugle uzrokuje beskonačno malo izduživanje niti.
Ovaj vam uređaj omogućuje simulaciju oscilacijskog gibanja takozvanog matematičkog njihala.
Sl. 1. Uređaj za proučavanje oscilacija matematičkog njihala: 1. Metalna ploča za utvrđivanje kuta otklona njihala; 2. Pokretna platforma; 3. Mjerno ravnalo.

Slika 2. Prikaz oscilatornih kretanja matematičkog njihala.
Zapravo, u početnom stanju nit je usmjerena vertikalno prema dolje (položaj 1 na slici 2). U ovom slučaju silaF napetost i čvrstoća nitimg težine lopte podudaraju se sa smjerom niti, ali suprotno usmjerene. Budući da se nit ne rasteže, obje sile međusobno se uravnotežuju, t.j.F \u003d mg ... Lopta miruje. To se stanje njihala naziva njegovim ravnotežnim položajem.
Izvadimo njihalo iz ravnotežnog položaja odbijajući kuglu od početnog stanja za kutφ 0 (slika 2). Zatim ga pustite bez naguravanja. Gravitacijommg lopta će se početi kretati prema položaju ravnoteže, nakon nekog vremena proći će je, a zatim će s druge strane ravnotežnog položaja odstupiti od nje za neki kut manji odφ 0 i pod djelovanjem gravitacije ponovno će jurnuti prema položaju ravnoteže. U nedostatku vanjskih utjecaja na loptu, ona će opisano kretanje izvesti u jednoj ravnini. Očito je da će putanja lopte biti luk kružnice polumjeral ... Ti se pokreti nazivaju vibracijama.
Zbog djelovanja sile otpora na kuglu prigušit će se njezine oscilacije, što dokazuje činjenica da će nakon svakog prolaska ravnoteže od nje odstupati pod sve manjim i manjim kutom. Međutim, ako se ovaj proces promatra prilično kratko vrijeme, tada se oscilatorni proces može prepoznati kao neomećen.
Razmotrite sile koje djeluju na loptu u proizvoljnom trenutkut. Neka je φ - kut otklona niti u ovom trenutku. Slijedi jednadžba Newtonovog drugog zakona u pravcuτ podudara se s tangentom povučenom na točku putanje lopte, u kojoj se ona nalazi u razmatranom trenutkut.
ma τ \u003d - mg sin φ (1)
Ovdje je τ - tangencijalno ubrzanje,m Je li masa kuglice. Znak minus s desne strane u (1) uzima u obzir činjenicu da pri kretanju iz ravnotežnog položaja prema gore sila gravitacije sprječava to kretanje.
Kutno ubrzanje ε lopte definirano je kao drugi vremenski izvod kutaφ, tj.
. (2)
Između tangencijalnog ubrzanjaa τ a kutna ε postoji očita veza
(3)
Jednadžba (1) uzimajući u obzir formule (2) i (3) ima oblik:
. (4)
U jednadžbi (4) nepoznata funkcijaφ (t) stoji pod znakom izvedenice drugog reda. Takva se jednadžba u matematici naziva običnom diferencijalnom jednadžbom drugog reda.
Može se pojednostaviti ako uzmemo u obzir da je pod malim kutovimaφ, mjereno u radijanima. Tada ćemo umjesto (4) imati
. (5)
Jednadžba (5) opisuje kretanje njihala. Naziva se i jednadžbom harmonijskog oscilatora.
Izravnom supstitucijom može se provjeriti ima li rješenje jednadžbe (5) oblik
, (6)
ako označimo sa
. (7)
Dakle, može se vidjeti da se promjene u kutuφ s vremenom se javlja prema sinusnom zakonu. Količinaφ 0 , jednaka maksimalnom kutu odstupanja od ravnotežnog položaja naziva se amplituda harmonijskih vibracija. Veličina amplitude u ovom slučaju ovisi o početnom odstupanju. Vrijednost pod sinusnim znakom naziva se faza. Faza raste proporcionalno vremenu. Vrijednost pod sinusnim znakom naziva se početna faza, koja je u razmatranom kretanju jednaka nuli.
Sinusna funkcija, koja određuje prirodu oscilatornih pokreta, periodična je funkcija s razdobljem jednakim. Ovo potonje znači da ako nakonT označimo razdoblje osciliranja njihala, tada za vrijednost faze možemo napisati sljedeću jednakost
, (8)
gdje je kutna frekvencija.
Sada, uzimajući u obzir (7) za to razdobljeImat ćemo:
(9)
Odnos (9) ukazuje da je linearizacija jednadžbe (4) dovela do jednadžbe (5), čije rješenje priznaje neovisnostT na amplitudi φ 0.
Takva se kolebanja nazivaju izokronima.
Formula (9) se također može predstaviti na sljedeći način:
k l, (10)
gdje kroz
(11)
označava nagib linearne funkcionalne ovisnosti funkcijeT 2 iz argumenta l.
Slijedom toga, izokronizam oscilacija njihala provjerava se valjanošću relacije (10) prema izmjerenim vrijednostima razdobljaT pri različitim vrijednostimal vezano za isti kutφ 0 .
Funkcionalna ovisnost, izvedena iz eksperimentalnih točaka, omogućuje određivanje nagibak, kroz čiju numeričku vrijednost ubrzanjeg slobodni pad lopte izračunava se na sljedeći način:
. (12)
Uz to, pojedinačnim mjerenjimaT i l ubrzanje g također se može izračunati iz ovog omjera:
(13)
III ... Postupak eksperimenta
Budući da se linearizacija jednadžbe (4), koja je dovela do jednadžbe (5), koja opisuje izokrone oscilacije, temelji na pretpostavci, očito je da je izokrono područje određeno vrijednostima kutaφ 0 kod kojih postoji linearna ovisnost.
Dakle, definirati raspon vrijednostiφ 0 , za koje vrijedi relacija (10), potrebno je za nekoliko vrijednostiφ 0 izvršiti mjerenja koja omogućuju crtanje ovisnosti, a zatim iz navedenih funkcionalnih ovisnosti izračunati nagibk i za odabrane kutoveφ 0 izračunati vrijednostig prema (12) i usporedite ih s općeprihvaćenom vrijednošćug \u003d 9,8 m / s 2. Ti kutovi φ 0 za koju je izračunata vrijednostg uzimajući u obzir pogrešku mjerenja, sačuvat će iste numeričke vrijednosti i odrediti opseg izokronizma oscilacija koje realizira ovaj uređaj.
Redoslijed mjerenja je sljedeći: odabire se određena vrijednost kutaφ 0 , kojim je potrebno skrenuti kuglu iz ravnotežnog položaja, postaviti se duljina njihala, izvesti pokus, tijekom kojeg se mjeri razdobljeT ... Pokus se izvodi nekoliko puta tako da pod fiksnim kutomφ 0 potrebno je imati od tri do pet izmjerenih vrijednostil i T.
Ovo će biti prva serija mjerenja u ravnini (T 2, l ) dat će samo jedan bod. Da biste provjerili formulu (10) pod zadanim kutomφ 0 potrebno je proizvesti nekoliko takvih serija.
Predlaže se napraviti pet takvih serija mjerenja za svaki od kutova.φ 0 , kao koji su odabrana sljedeća tri kuta:φ 0 \u003d 10 oko; φ 0 \u003d 20 oko; φ 0 \u003d 30 o.
Višestruko izmjerene vrijednostil i T za odabrani kutφ 0 njihove aritmetičke sredine izračunavaju se prema formulama:
, (14)
gdje je n - broj mjerenja.
Kao rezultat mjerenja, student mora ispuniti sljedeće tri tablice eksperimentalnim podacima i pokazati ih učitelju.
Stol 1.
|
φ 0 \u003d 10 o |
||||||||||
|
mjerni broj |
serija 1 |
serija 2 |
serija 3 |
serija 4 |
epizoda 5 |
|||||
Tablica 2.
|
φ 0 \u003d 20 o |
||||||||||
|
mjerni broj |
serija 1 |
serija 2 |
serija 3 |
serija 4 |
epizoda 5 |
|||||
Tablica 3.
|
φ 0 \u003d 30 o |
||||||||||
|
mjerni broj |
serija 1 |
serija 2 |
serija 3 |
serija 4 |
epizoda 5 |
|||||
Pri mjerenju duljinel njihala, mora se imati na umu da se potonji sastoji od duljine niti koja drži loptu i radijusa kuglice.
Polumjer kuglice izračunava se kroz njezin promjer, koji se mjeri nonierskim kaliperom. Budući da kugla ne predstavlja idealnu sfernu površinu, svako mjerenje promjera dobit će vrijednost koja se malo razlikuje od prethodno izmjerene.
Uređaj, koji provodi oscilacijska kretanja njihala, ima uređaj koji regulira duljinu niti. U ovom se slučaju duljina konca može mjeriti na dva načina: ili primijeniti referentni konac na konac fiksne duljine, čija se duljina zatim mora izmjeriti na mjernom ravnalu; ili uzmite nit određene duljine kao referentnu nit i fiksirajte duljinu niti njihala uz pomoć podesivog uređaja ovog uređaja.
Pokretna platforma (vidi sliku 1.) omogućuje vam mjerenje duljine njihala na drugi način. Da biste to učinili, potrebno je kombinirati navoj njihala s kuglom s gornjom ravninom pomične platforme (vidi sliku 3) Isti položaj platforme može se učvrstiti na mjernom ravnalu - to će biti duljina niti zajedno s kuglom, od koje se mora oduzeti polumjer kuglice. Promjer lopte mora se izmjeriti čeljusti za nonier.

Sl. 3.
Razdoblje T Oscilacije njihala najbolje je definirati na sljedeći način: izmjerite vrijemet nekoliko oscilacija njihala, a zatim podijelite ovo vrijeme s brojem oscilacija. Treba imati na umu da vrijeme jednog osciliranja znači vrijeme tijekom kojeg se lopta vraća iz jednog od krajnjih položaja u isti položaj.
Za postavljanje potrebnog kutaφ 0 potrebno je koristiti pravokutnu metalnu ploču na kojoj iz jedne točke izlazi nekoliko vodilica, nagnutih pod različitim kutovima okomitoj crti koja izvire iz te točke. Ti se kutovi mogu mjeriti kutomjerom.
Pokretna platforma omogućuje poravnavanje pravokutne ploče s točkom ovjesa niti njihala tako da se okomita crta na ploči poklapa s navojem njihala kada je lopta u donjem položaju.
Nakon ovog poravnanja, pokretna platforma zajedno s pločom može se učvrstiti. Sada, kada je nit nagnuta pod jednim ili drugim kutom, mora se poravnati s jednom od linija ploče koja definira određeni kut (vidi sliku 1)
IV ... Obrada rezultata mjerenja
Bilo koja od izmjerenih vrijednostil i T prikazani u tablicama 1-3 nisu točne vrijednosti jer se mjere s određenim pogreškama.
U takvim se slučajevima aritmetičke sredine izračunate formulama (14) uzimaju kao točne vrijednosti naznačenih veličina. Tada pod pogreškom mjerenja podrazumijevamo modul maksimalnog odstupanja svih izmjerenih vrijednosti od njihove aritmetičke sredine. Naime, pogreška ∆1 mjerenja duljine njihala definirat će se kao
∆ 1 \u003d maks. | l i - l cf |, (15)
a pogreška ∆ 2 - razdoblje oscilacije njihala treba izračunati kako slijedi:
∆ 2 \u003d maks. | T i - T av | ... (16)
U formulama (15) - (16) indeksja \u003d 1,2,3… prolazi kroz sve mjerne brojeve odgovarajućih veličina.
Rezultate mjerenja obradit ćemo na računalu u programuMicrosoft Excel a mi ćemo pokazati tehnologiju potrebnih izračuna na temelju određenih rezultata mjerenja.
Neka se Tablica 3 ispuni sljedećim stvarnim podacima.
Tablica 3
|
φ 0 \u003d 30 o |
||||||||||
|
mjerni broj |
serija 1 |
serija 2 |
serija 3 |
serija 4 |
epizoda 5 |
|||||
|
0,505 0,495 0,503 0,498 0,500 |
1,434 1,434 1,428 1,422 1,418 |
0,606 0,594 0,603 0,597 0,600 |
1,547 1,553 1,557 1,575 1,553 |
0,704 0,696 0,702 0,698 0,700 |
1,685 1,681 1,678 1,691 1,687 |
0,806 0,794 0,804 0,797 0,800 |
1,807 1,815 1,791 1,791 1,800 |
0,904 0,896 0,903 0,898 0,900 |
1,907 1,909 1,925 1,906 1,897 |
|
Za svaku seriju mjerenja potrebno je izračunati pomoću formula (14)l av i T av a zatim izgraditi ovisnostT cf 2 \u003d f (l cf) ... Radi praktičnosti uvodimo zapis:T cf 2 \u003d y 1, l cf \u003d x 1.
Prije nastavka na naznačene izračune, konstruiramo u programuExcel tablicu 3 i pripremite format tablice 4, čiji će se podaci koristiti pri konstrukciji funkcionalne ovisnostiy 1 \u003d f (x 1).
U Excelu Tablica 3 oblikovana je kako slijedi.
Na listu 1 radne bilježniceExcel aktivirati niz stanica stanicaA 1: A 2, spojite ih i unesite naslov prvog stupca u rezultirajuću spojenu ćeliju s tipkovnice: “n mjerni broj", Aktiviraj raspon ćelijaB 1: C 1, spojite ih i unesite zajedničko zaglavlje drugog i trećeg stupca u rezultirajuću spojenu ćeliju s tipkovnice: “serija 1 ", Aktiviraj ćelijuB 2 i u njega unesite podnaslov drugog stupca tablice 3 s tipkovnice: “l "Nakon toga aktiviramo ćeliju C2 i s tipkovnice u nju unosimo podnaslov trećeg stupca tablice 3:"T ". Ponovimo naznačene radnje za preostale stupce tablice 3. Kao rezultat izvršavanja gore navedenih radnji, dobili smo format tablice 3.
Sada ispunimo dobiveni format podacima iz tablice 3, što rezultira dobivanjem tablice 3 u programuExcel.

Za izgradnju formata tablice 4 u programuExcel na listu1 radne bilježniceExcel aktivirati stanicuA 9 i unesite zaglavlje prvog stupca u njega s tipkovnice: “n B 9 i unesite zaglavlje drugog stupca u njega s tipkovnice: “l cf \u003d x 1 ". Slično tome, s tipkovnice unosimo zaglavlja trećeg, četvrtog i petog stupca: „T cf "," T cf 2 \u003d y 1 "i" y 1 / x 1 "u ćelijama C 1, D 1 i E 1 odnosno. Zatim aktivirajte ćelijuA 10 i u njega unesite broj 1 s tipkovnice, u ćelijuA 11 znamenki 2, aktivirajte raspon ćelijaA 10: A 11 i samodovršetak do ćelijeA 14. Kao rezultat izvršavanja gore navedenih radnji dobivamo tablicu 4.
Tablica 4.
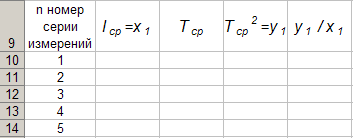
Pokazati ćemo tehnologiju popunjavanja prvog reda tablice 4 obradom mjerenja serije 1.
Za koje programiramo prvu formulu u (14), dobivamol srijeda i stavite u tablicu 4.B 10 i s tipkovnice unesite formulu "\u003d SUM (B3: B7) * (1/5)".
Zatim programiramo drugu formulu u (14).E 2 i s tipkovnice unesite formulu "\u003d SUM (C3: C7) * (1/5)".
Dobivamo T usp i kvadrat, a zatim izračunajte omjer. Da biste to učinili, aktivirajte ćelijuD 10 i s tipkovnice unesite formulu "\u003d C10 ^ 2", a zatim aktivirajte ćelijuE 10 i s tipkovnice unesite formulu "\u003d D10 / B10". Nakon svih ovih radnji, prvi red tablice 4 dobiva oblik

Nakon ponavljanja gornjih izračuna za ostale serije, Tablica 4 dobiva konačni oblik
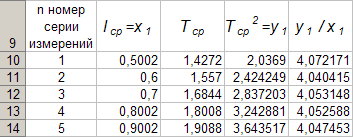
Podaci u tablici 4. omogućuju korištenje programaExcel izgraditi graf funkcionalne ovisnostiy 1 \u003d f (x 1).
Da biste to učinili, aktivirajte raspon stanicaD 10: D 14, nazovimo čarobnjaka za programske funkcijeExcel , odaberite vrstu grafikona "Scatter", prvi prikaz. Pomaknite kursor miša na gumb "Dalje" i izvedite jedan klik lijevom tipkom miša (LMB). Nakon toga idite na karticu Red. Da biste to učinili, pomaknite kursor miša na karticu "Red" koja se nalazi u gornjem dijelu prozora "Čarobnjak za grafikone" i izvedite jedan klik LMB-a. Zatim postavite kursor u polje "X vrijednosti", a zatim pomaknite kursor miša u ćelijuB 10, pritisnite LMB i bez puštanja pomaknite kursor miša do ćelijeB 14, a zatim otpustite LMB. Kao rezultat, formula „\u003d Sheet1! $10 B $: B 14 dolara ". Sada pomaknite kursor miša na gumb "Dalje" i izvedite dva LMB klika zaredom, a zatim pomaknite kursor miša na gumb "Završi" i izvedite jedan LMB klik. Na listu 1 radne bilježniceExcel pojavit će se grafikon funkcionalne ovisnostiy 1 \u003d f (x 1) ... Aktiviramo redak 10 i dodamo novi redak, nakon čega ulazimo s tipkovnice u staniceA 10: E 10-znamenkasti "0". Zatim pomaknite kursor miša na bilo koju točku na grafikonu i izvedite jedan klik LMB-a. Povećajmo raspon podataka grafikona, za koji pomičemo kursor miša do granice raspona vrijednostiy 1 i pomaknite marker koji se nalazi u gornjem desnom kutu obruba do ćelijeD 10. Učinimo isto s dometomx 1.
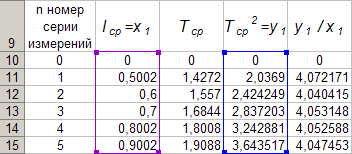
Sada pomaknite kursor miša na bilo koju točku na grafikonu i izvedite jedan desni klik (RMB). U kontekstnom izborniku koji se pojavi pomaknite kursor miša na naredbu "Dodaj liniju trenda" i izvedite jedan LMB klik. Slika 4 ilustrira rezultat ovih konstrukcija.
Slika 4.
Slika 4 implicira da ovisnosty 1 \u003d f (x 1) je linearna i opisuje se jednadžbom
y 1 \u003d 4,04 8 x 1 + 0,00 24 (17)
Jednadžba 17 pokazuje da je nagibk iz jednadžbe (10) ispada jednako:k \u003d 4,0493. Ako je ova vrijednostk supstituiran u formuli (12), tada dobivamo vrijednost ubrzanja gravitacije.
Nagibk u jednadžbi (10) može se izračunati iz podataka u tablici 4 formulom
(18)
Da biste to učinili, aktivirajte ćelijuA 17 i unesite formulu „\u003d SUM (E 11: E 15) * (1/5) "
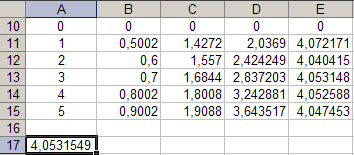
dobivamo k \u003d 4,053, tj. broj blizak brojuk dobiveno iz grafa prikazanog na slici 4.
Očito je da je broj dobiven formulom (12) koristeći količinuk iz jednadžbe (17) imat će neku pogrešku.
Da bismo izračunali ovu pogrešku, vratimo se podacima u tablicama 3 i 4.
Prvo u programuExcel stvorite format za novu tablicu 5. Zašto na Sheet1 radne knjigeExcel aktivirati stanicuA 19 i unesite zaglavlje prvog stupca u njega s tipkovnice: “n mjerni broj serije ", aktiviraj ćelijuB 19 i s tipkovnice u njega unesite naslov drugog stupca: „∆1 prema (15) ". Isto tako, s tipkovnice unesite zaglavlja trećeg stupca: „∆2 prema (16) "u ćeliju C 19. Zatim aktivirajte ćelijuA 20 i u njega unesite broj 1 s tipkovnice, u ćelijuA 21 znamenka 2, aktivirajte raspon ćelijaA 20: A 21 i samodovršava do ćelijeA 26. Kao rezultat izvršavanja gore navedenih radnji dobivamo tablicu 5.
Tablica 5.

Pri programiranju formula (15) i (16) to je neophodnol i i T i za svaku seriju mjerenja iz tablice 3 il av i T av iz podataka u tablici 4.
Za izračun ∆1 za prvu seriju mjerenja potrebno je aktivirati stanicuM 3 i u njega unesite formulu "\u003d ABS (B3-B $ 11))" s tipkovnice, a zatim ćemo automatski dovršiti do ćelijeM 7. Sada u ćelijuB 20 unijet ćemo s tipkovnice formulu "\u003d MAX (M3: M7)".
Za izračun ∆2 prema podacima iz iste serije potrebno je aktivirati stanicuN 3 i u njega unesite formulu "\u003d ABS (C3-C $ 11)" s tipkovnice, nakon čega ćemo se automatski dopuniti do ćelijeN 7. Sada u ćelijuC 20 unijet ćemo s tipkovnice formulu "\u003d MAX (N3: N7)".
Kao rezultat, tablica 5. ima oblik

Nakon izvođenja proračuna prema (15) i (16) za podatke iz drugih serija mjerenja, tablica 5 dobiva oblik
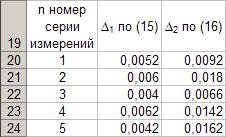
Iz podataka u tablici 5. očito je da su za svaku seriju mjerenja točne vrijednosti duljinel njihalo i razdobljeT Oscilacije njihala definirane su kako slijedi
l \u003d l av ± ∆ 1, T \u003d T av ± ∆ 2 (19)
Štoviše, ispada da je ∆1 i ∆ 2 se razlikuju za svaku od duljina njihala. Iz formula (19) proizlazi da je ravna crta na slici 4 povučena s pogreškom i u njezinoj blizini postoji takozvani raspršeni eksperimentalni podatak.
Da bismo uzeli u obzir raspršenost eksperimentalnih podataka, izračunajmo još dvije funkcionalne ovisnosti:
(T avg + ∆ 2) 2 \u003d f (l av + ∆ 1), (20)
(T av - ∆ 2) 2 \u003d f (l av - ∆ 1). (21)
Za izračunavanje ovisnosti (20) uvodimo nove oznake:
x 2 \u003d (l cf + ∆ 1), (22)
y 2 \u003d (T prosječno + ∆ 2) 2, (23)
Prije nastavka izračunavanja pomoću formula (22) i (23), oblikujemo format nove tablice 6 pomoću programaExcel , prema prethodno naznačenom algoritmu, Tada dobivamo
Tablica 6.
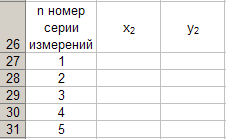
Pri izračunavanju x 2 i y 2 prema (22) i (23), potrebno je koristiti podatke iz tablica 4 i 5. Prvo izračunavamox 2 a dobiveni brojevi unose se u tablicu 6.
Da biste to učinili, aktivirajte ćelijuB 27 i u njega unesite formulu "\u003d B11 + B20" s tipkovnice.
Zatim izračunajte y 2 za to aktiviramo stanicuC 27 i u njega unesite s tipkovnice formulu "\u003d (C11 + C20) ^ 2".
B 27: C 27 i samodovršava do ćelijeC 31.
Tada će se tablica 6 popuniti sljedećim podacima
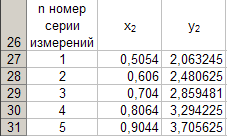
Prema tablici 6, gradimo grafikon ovisnostiy 2 \u003d y 2 (x 2) (vidi sliku 5) prema prethodno opisanoj tehnologiji
Slika 5 pokazuje da ovisnosty 2 \u003d y 2 (x 2) određuje se jednadžbom
y 2 \u003d 4,08 86 x 2 - 0,002 3 (24)
Prelazimo na izračunavanje funkcionalne ovisnosti (21). Za to uvodimo dvije pomoćne formule
x 3 \u003d l cf - ∆ 1, (25)
y 3 \u003d (T av - ∆ 2) 2. (26)
Izračun prema ovim formulama vrši se prema podacima iz tablica 4 i 5, a rezultati tih izračuna unose se u tablicu 7. Prvo izračunavamox 3 ... Da biste to učinili, aktivirajte ćelijuB 34 i u njega unesite formulu "\u003d B11-B20" s tipkovnice.
Zatim izračunajte y 3 za to aktiviramo stanicuC 34 i u nju unesite formulu "\u003d (C11-C20) ^ 2" s tipkovnice.
Aktivirajmo sada raspon stanica.B 34: C 34 i samodovršava u ćelijuC 38.
Podaci u ovoj tablici su sljedeći
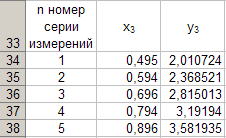
Funkcionalna ovisnostg 3 = g3 (x3 ) , izgrađena prema podacima iz tablice 7, prikazana je na slici 6.
Slika 6 implicira da
g3 = 4,00 7 3 x3 + 0,00 71 (27)
Vrijednosti nagibak prema podacima jednadžbi (17), (24), (27) unosimo u tablicu 8.

Programiramo formulu (12) i izračunavamogkoja odgovara svakoj vrijednostik... Upisujemo dobivene vrijednostig u tablici 8. Da biste to učinili, aktivirajte ćelijuC41 i s tipkovnice unesite formulu "\u003d (4 * PI () ^ 2) / B41". Nakon toga ćemo se automatski dopuniti do ćelijeC43.
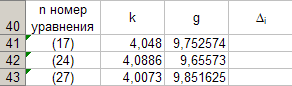
Sada izračunavamo prosjekg prema formuli
Da biste to učinili, aktivirajte ćelijuC45 i u njega unesite formulu "\u003d (1/3) * SUM (C41: C43)" s tipkovnice.

Ispada da je jednako 9,75331, što uzimamo kao točnu vrijednost. Pogreška u određivanju ove vrijednostig izračunato po formuli
Δ 3 = maks | gja goženiti se| = maks | Δ ja| (28)
Da biste to učinili, aktivirajte ćelijuD41 i u njega unesite formulu "\u003d ABS (C41-C $ 45)" s tipkovnice. Nakon toga ćemo se automatski dopuniti do ćelijeD43.

IzračunavamoΔ ja i stavite je u tablicu 8. Da biste to učinili, aktivirajte ćelijuD45 i s tipkovnice unesite formulu "\u003d MAX (D41: D43)".
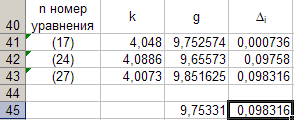
Iz podataka u tablici 8 proizlazi daΔ 3 \u003d 0,098316. Dakle, ubrzanjeg slobodni pad dobiven ovim uređajem, kao rezultat neizravnih mjerenja, pokazao se jednakim
g \u003d 9,7533 ± 0,0983.
ispitna pitanja
- Koji su elementi uređaja za proučavanje oscilacija matematičkog njihala.
- Na temelju kojeg je zakona mehanike sastavljena jednadžba gibanja njihala.
- Koja su ograničenja pod kojima se dobiva jednadžba koja simulira kretanje matematičkog njihala.
- Koje se vibracije nazivaju harmonijskim.
- Dajte definiciju amplitude, faze i učestalosti oscilacija.