I. Определение, основни свойства и графики на хиперболични функции. Хиперболични функции Th математическа функция
11 Основни функции на комплексна променлива
Нека си припомним определението на комплексния показател -. Тогава
Разширяване на серия Maclaurin. Радиусът на сходимост на тази серия е + ∞, което означава, че комплексната степен е аналитична върху цялата комплексна равнина и
(exp z) "= ехр z; ехр 0 = 1. (2)
Първото равенство тук следва, например, от теоремата за диференциация член по член за степенен ред.
11.1 Тригонометрични и хиперболични функции
Синусова комплексна променливанаречена функция

Косинус на комплексна променливаима функция

Хиперболичен синус на комплексна променливадефиниран така:
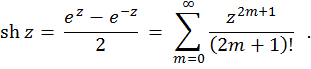
Хиперболичен косинус на комплексна променливае функция

Нека отбележим някои свойства на нововъведените функции.
А.Ако x∈ ℝ, тогава cos x, sin x, ch x, sh x∈ ℝ.
Б.Съществува следната връзка между тригонометричните и хиперболичните функции:
cos iz = ch z; sin iz = ish z, ch iz = cos z; sh iz = isin z.
Б. Основни тригонометрични и хиперболични идентичности:
cos 2 z + sin 2 z = 1; ch 2 z-sh 2 z = 1.
Доказателство за основната хиперболична идентичност.
Основната тригонометрична идентичност следва от основната хиперболична идентичност, когато се вземе предвид връзката между тригонометрични и хиперболични функции (виж свойство B)
Г Формули за събиране:
В частност,
Д.За да се изчислят производните на тригонометрични и хиперболични функции, трябва да се приложи теоремата за диференцирането член по член на степенен ред. Получаваме:
(cos z) "= - sin z; (sin z)" = cos z; (ch z) "= sh z; (sh z)" = ch z.
Е.Функциите cos z, ch z са четни, а функциите sin z, sh z са нечетни.
G. (Периодичност)Функцията e z е периодична с период 2π i. Функциите cos z, sin z са периодични с период 2π, а функциите ch z, sh z са периодични с период 2πi. Освен това,
Прилагайки формулите за сумата, получаваме
З. Разлагане на реални и въображаеми части:
Ако еднозначна аналитична функция f (z) преобразува биективно област D в област G, тогава D се нарича област на schlichtness.
И.Домейн D k = (x + iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
Доказателство. От съотношение (5) следва, че отображението exp: D k → ℂ е инжекционно. Нека w е произволно ненулево комплексно число. Тогава, решавайки уравненията e x = | w | и e iy = w / | w | с реални променливи x и y (изберете y от половин интервал)