I. ഹൈപ്പർബോളിക് ഫംഗ്ഷനുകളുടെ നിർവ്വചനം, അടിസ്ഥാന ഗുണങ്ങളും ഗ്രാഫുകളും. ഹൈപ്പർബോളിക് ഫംഗ്ഷനുകൾ Th ഗണിത പ്രവർത്തനം
11 സങ്കീർണ്ണമായ വേരിയബിളിന്റെ അടിസ്ഥാന പ്രവർത്തനങ്ങൾ
കോംപ്ലക്സ് എക്സ്പോണന്റിന്റെ നിർവചനം നമുക്ക് ഓർമ്മിക്കാം -. പിന്നെ
മക്ലൗറിൻ സീരീസ് വിപുലീകരണം. ഈ ശ്രേണിയുടെ സംയോജനത്തിന്റെ ആരം + ∞ ആണ്, അതിനർത്ഥം സങ്കീർണ്ണമായ എക്സ്പോണന്റ് മുഴുവൻ സങ്കീർണ്ണ തലത്തിലും വിശകലനം ചെയ്യുന്നു എന്നാണ്.
(exp z) "= exp z; exp 0 = 1. (2)
ഇവിടെ ആദ്യത്തെ സമത്വം പിന്തുടരുന്നു, ഉദാഹരണത്തിന്, ഒരു പവർ സീരീസിനുള്ള ടേം-ബൈ-ടേം ഡിഫറൻഷ്യേഷൻ സിദ്ധാന്തത്തിൽ നിന്ന്.
11.1 ത്രികോണമിതി, ഹൈപ്പർബോളിക് പ്രവർത്തനങ്ങൾ
സൈൻ കോംപ്ലക്സ് വേരിയബിൾഫംഗ്ഷൻ വിളിച്ചു

ഒരു സങ്കീർണ്ണ വേരിയബിളിന്റെ കോസൈൻഒരു ചടങ്ങുണ്ട്

ഒരു സങ്കീർണ്ണ വേരിയബിളിന്റെ ഹൈപ്പർബോളിക് സൈൻഇതുപോലെ നിർവചിച്ചിരിക്കുന്നു:
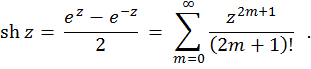
ഒരു സങ്കീർണ്ണ വേരിയബിളിന്റെ ഹൈപ്പർബോളിക് കോസൈൻഒരു ചടങ്ങാണ്

പുതുതായി അവതരിപ്പിച്ച ഫംഗ്ഷനുകളുടെ ചില സവിശേഷതകൾ നമുക്ക് ശ്രദ്ധിക്കാം.
എ. x∈ ℝ ആണെങ്കിൽ, cos x, sin x, ch x, sh x∈ ℝ.
ബി.ത്രികോണമിതിയും ഹൈപ്പർബോളിക് ഫംഗ്ഷനുകളും തമ്മിൽ ഇനിപ്പറയുന്ന ബന്ധമുണ്ട്:
cos iz = ch z; sin iz = ish z, ch iz = cos z; sh iz = isin z.
B. അടിസ്ഥാന ത്രികോണമിതിയും ഹൈപ്പർബോളിക് ഐഡന്റിറ്റികളും:
cos 2 z + sin 2 z = 1; ch 2 z-sh 2 z = 1.
പ്രധാന ഹൈപ്പർബോളിക് ഐഡന്റിറ്റിയുടെ തെളിവ്.
ത്രികോണമിതിയും ഹൈപ്പർബോളിക് ഫംഗ്ഷനുകളും തമ്മിലുള്ള ബന്ധം കണക്കിലെടുക്കുമ്പോൾ പ്രധാന ഹൈപ്പർബോളിക് ഐഡന്റിറ്റിയിൽ നിന്ന് പ്രധാന ത്രികോണമിതി ഐഡന്റിറ്റി പിന്തുടരുന്നു (പ്രോപ്പർട്ടി ബി കാണുക)
ജി കൂട്ടിച്ചേർക്കൽ സൂത്രവാക്യങ്ങൾ:
പ്രത്യേകിച്ച്,
ഡി.ത്രികോണമിതി, ഹൈപ്പർബോളിക് ഫംഗ്ഷനുകളുടെ ഡെറിവേറ്റീവുകൾ കണക്കാക്കാൻ, ഒരു പവർ സീരീസിന്റെ ടേം-ബൈ-ടേം ഡിഫറൻഷ്യേഷനിൽ ഒരാൾ സിദ്ധാന്തം പ്രയോഗിക്കണം. നമുക്ക് ലഭിക്കുന്നത്:
(cos z) "= - sin z; (sin z)" = cos z; (ch z) "= sh z; (sh z)" = ch z.
ഇ. cos z, ch z എന്നീ ഫംഗ്ഷനുകൾ ഇരട്ടയാണ്, കൂടാതെ sin z, sh z എന്നീ ഫംഗ്ഷനുകൾ വിചിത്രവുമാണ്.
ജി. (ആവർത്തനകാലം) e z ഫംഗ്ഷൻ 2π i കാലയളവുള്ള ആനുകാലികമാണ്. cos z, sin z എന്നീ ഫംഗ്ഷനുകൾ 2π കാലയളവുള്ള ആനുകാലികവും, ch z, sh z എന്നീ ഫംഗ്ഷനുകൾ 2πi കാലയളവിലുള്ള ആനുകാലികവുമാണ്. മാത്രമല്ല,
സം സൂത്രവാക്യങ്ങൾ പ്രയോഗിക്കുമ്പോൾ, നമുക്ക് ലഭിക്കും
Z. യഥാർത്ഥവും സാങ്കൽപ്പികവുമായ ഭാഗങ്ങളായി വിഘടിപ്പിക്കുന്നു:
ഒരൊറ്റ മൂല്യമുള്ള അനലിറ്റിക് ഫംഗ്ഷൻ f (z) ഒരു ഡൊമെയ്ൻ D-യെ ഒരു ഡൊമെയ്നിലേക്ക് മാപ്പ് ചെയ്യുന്നുവെങ്കിൽ, D-യെ schlichtness എന്ന ഡൊമെയ്ൻ എന്ന് വിളിക്കുന്നു.
ഒപ്പം.ഡൊമെയ്ൻ D k = (x + iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
തെളിവ്. മാപ്പിംഗ് എക്സ്പ്രസ്: D k → ℂ injective ആണെന്ന് ബന്ധത്തിൽ നിന്ന് (5) ഇത് പിന്തുടരുന്നു. w ഏതെങ്കിലും പൂജ്യമല്ലാത്ത സങ്കീർണ്ണ സംഖ്യയായിരിക്കട്ടെ. തുടർന്ന്, e x = | w | എന്ന സമവാക്യങ്ങൾ പരിഹരിക്കുന്നു ഒപ്പം e iy = w / | w | യഥാർത്ഥ വേരിയബിളുകൾ x, y എന്നിവ ഉപയോഗിച്ച് (അർദ്ധ ഇടവേളയിൽ നിന്ന് y തിരഞ്ഞെടുക്കുക)