I.双曲線関数の定義、基本的なプロパティ、およびグラフ。 双曲線関数Th数学関数
11複素変数の基本機能
複素指数の定義を思い出してみましょう-。 それで
マクラウリン級数展開。 この級数の収束半径は+∞です。これは、複素指数が複素平面全体で分析的であり、
(exp z) "= exp z; exp 0 = 1.(2)
ここでの最初の等式は、たとえば、べき級数の項ごとの微分定理から得られます。
11.1三角関数と双曲線関数
サイン複素変数関数と呼ばれる

複素変数の正弦機能があります

複素変数の双曲線正弦このように定義されます:
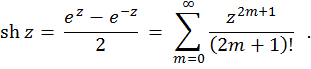
複素変数の双曲線正弦関数です

新しく導入された関数のいくつかのプロパティに注目しましょう。
A。 x∈ℝの場合、cos x、sin x、ch x、shx∈ℝ。
B。三角関数と双曲線関数の間には、次のような関係があります。
cos iz = ch z; sin iz = ish z、ch iz = cos z; sh iz = isinz。
B.基本的な三角法と双曲線の恒等式:
cos 2 z + sin 2 z = 1; ch 2 z-sh 2 z = 1。
主な双曲線恒等式の証明。
主な三角関数の恒等式は、三角関数と双曲線関数の間の関係を考慮に入れると、主な双曲線の恒等式に従います(プロパティBを参照)。
G 加算式:
特に、
D。三角関数と双曲線関数の導関数を計算するには、べき級数の項ごとの微分に定理を適用する必要があります。 我々が得る:
(cos z) "= --sin z;(sin z)" = cos z; (ch z) "= sh z;(sh z)" = chz。
E。関数cosz、ch zは偶数であり、関数sin z、shzは奇数です。
G.(周期性)関数ezは、2πiの周期で周期的です。 関数cosz、sin zは2πの周期で周期的であり、関数ch z、shzは2πiの周期で周期的です。 さらに、
合計式を適用すると、次のようになります。
Z. 実数部と虚数部への分解:
単一値の分析関数f(z)がドメインDをドメインGに全単射で写像する場合、Dは定義域と呼ばれます。
と。ドメインDk =(x + iy |2πk≤y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
証拠。 関係式(5)から、写像exp:Dk→ℂは単射であることがわかります。 wをゼロ以外の複素数とします。 次に、方程式e x = | w |を解きます。 およびeiy = w / | w | 実変数xおよびyを使用(半区間からyを選択)