Def . Let be ,
,

.

The set is called a closed gap or closed bar in .

The set is called an open gap

or an open bar in .

Def . Measure of intervals and the quantity is called:

(More precisely
).

Def . If
such that
then the interval is called degenerate and
.

Spacing measure properties:

a). Positivity:
, and
if and only if - is degenerate.

b). Positive uniformity:.

v). Additivity:

* for
such that
;

* for
and

.

G). Monotonicity of measure:.

Def . The diameter of the bar (gap) is the value:

Note that
and
Are not the same thing. For example, if - degenerate, then
, a
(generally speaking).

Wherein: * ;

* ;*
.

Def . The aggregate
sub-spacing is called splitting the interval , if: *;

*
; *
; *
; *
.

The quantity
is called the partition parameter P(wherein
).

Def . Splitting is called refining the partition if all elements of the partition obtained by splitting the split elements .

It is indicated:
... Read: smaller or larger .

For the larger-smaller relationship, it is true:

*. transitivity -; *.
;

*.


; *.

|
.

§. Definition of multiple integral

Let be
- timber (gap) in ,
- splitting the gap I... At each of the intervals of the partition mark the point
.

We get
split with marked points for
.

The quantity
is called the integral Riemann sum for the function f (x) on the interval I by split with marked points
.

Def :
=
=
.

Denoting - a set of functions integrable on a bar I we write down:

Def : ε > 0 δ>0<.

If for the function f(x) on I and splitting
- denote by
- the highest and the lowest value of the function f(x) on I k then the quantities
=
and
=
are called the lower and upper Darboux sums.

§. Darboux criterion for the existence of a multiple integral.

T 0 . To function
was integrable on a bar (those.
) is necessary and sufficient that

. Δ▲.

Integration of the function over a bar in Euclidean space is determined. How to integrate the function over an arbitrary bounded set from Euclidean space?

Let us define the integral of the function f by the set
.

Def : Let be
and
- limited, i.e.
... Function
is called the characteristic function of the set M.

Then:
≡
.

The definition of an integral over a set does not depend on which bar containing M selected, i.e.

.

This means that the definition of an integral over a set is correct.

A necessary condition for integrability. To function f(x) on M be integrable, it is necessary that f(x) was limited to M. Δ▲.

§. Properties of multiple integrals.

1  . Linearity: Many R M functions integrable on the set M - linear

space, and
- linear functional.

2  . Normalization condition:
... Another form of notation
in fact determines the measure of an arbitrary set from Euclidean space.

3  . If the integral over a set of Lebesgue measure zero exists, then it

is zero.

Note: Lots of M is called the set of Lebesgue measure zero,

if

such that
and
.

4  . a.;b.;

v. if
and - separated from zero by M, then

5  .
and f=g p.c. (almost everywhere) on M, then
.

6  . Additivity: If
and
then

,

In general:
.

Δ. Follows from equality: ▲

7  . Monotone:
and
then
.

8  . Integration of inequalities: if
ito

.

9  . Let be


... To
, it is necessary and sufficient that there is an interior point of the set M, wherein f (x)> 0 and is continuous.

10  . Integrability of the module of the function being integrated:
.

11  . Average theorem:
,
on M preserves the sign and
, then

.

If the set M- connected and f(x) Is continuous on
then
such that
.

12  . In order for the integral of a non-negative function to be equal to 0

necessary and sufficient to f(x) = 0 almost everywhere on M.

13  . Fubini's theorem. For double integral:

Let the region
- rectangle:. Then, under the condition of the existence of internal single integrals, to find the double integral, one can proceed to repeated integration (see Fig. A):

, or

E

If the domain of integration is not a rectangle, Fubini's theorem is still valid and has the form (see Fig. b):
. (*)

Note: The external limits of integration should be constants, the internal limits of integration may depend on the variable over which the integration is still to be done.

Formula (*) can be obtained using the characteristic function of the set D.

For multiple integral:

Let some subsets of Euclidean spaces and ... We define the Cartesian product of these sets, which is a subset of the Euclidean space
:.

Then Fubini's theorem for
looks like:
.

The theorem is also valid for the bars X and Y, and for more complex configurations.

Examples:

1 0 . Calculate
if the border of the region
given by the equations:

... Finding the intersection points of the curves defining the boundary of the region, we get two points:
and
... Then the possible arrangement of the limits of integration when passing to iterated integrals gives:

a).
;

2

0 . Change the order of integration in the re-integral:
.

–

.

Recipe: When setting the limits of integration in a double integral, it is recommended to start with the outer limits of integration.

3

0 . Calculate:
, if

Passing to iterated integrals gives:
.

In this case, in the triple integral, the arrangement of the limits must begin with the internal limits of integration. Then project the area V on the plane xOy

setting limits in the area D- lying in the plane xOy.

4 0 . Change the order of integration in the re-integral:
.

Let us dwell in somewhat more detail on Ostrogradskii's works on multiple integrals.

Ostrogradsky's formula for transforming a triple integral into a double integral, which we usually write in the form

where div A is the divergence of the field of the vector A,

An is the scalar product of the vector A by the unit vector of the outward normal n of the boundary surface; in the mathematical literature it was often associated earlier with the names of Gauss and Green.

In fact, in Gauss's work on the attraction of spheroids, one can see only very special cases of formula (1), for example, for P = x, Q = R = 0, etc. As for J. Green, in his work on the theory of electricity and there is no magnetism of formula (1) at all; it derived another relation between triple and double integrals, namely, Green's formula for the Laplace operator, which can be written in the form

Of course, one can derive formula (1) from (2) by setting

and in the same way you can get formula (2) from formula (1), but Green did not even think of doing this.

where the integral over the volume is on the left, and the integral over the boundary surface is on the right, and these are the direction cosines of the outer normal.

The Parisian manuscripts of Ostrogradskiy testify with complete certainty that both the discovery and the first communication of the integral theorem (1) belonged to him. For the first time it was expressed and proved, exactly as it is done now in the "Proof of a theorem of integral calculus" presented to the Paris Academy of Sciences on February 13, 1826, after which it was again formulated in that part of the "Memoir on the propagation of heat inside solids”, Which Ostrogradsky presented on August 6, 1827.“ Memoir ”was given to Fourier and Poisson for review, and the latter certainly read it, as evidenced by the entry on the first pages of both parts of the manuscript. Of course, Poisson did not even think to ascribe to himself the theorem, which he met in the work of Ostrogradsky two years before the presentation of his work on the theory of elasticity.

As for the relationship between the works on multiple integrals of Ostrogradskii and Green, we recall that in the "Note on the Theory of Heat" a formula was derived that embraces Green's own formula, as a very special case. The now unusual symbolism of Cauchy, used by Ostrogradsky in the "Note", until recently hid this important discovery from researchers. Of course, Greene retains the honor of the discovery and the first publication in 1828 of the formula for the Laplace operators bearing his name.

The discovery of the formula for the transformation of a triple integral into a double integral helped Ostrogradskii solve the problem of varying the n-fold integral, namely, to derive the general formula for the transformation of the integral of an expression of the type of divergence over the n-dimensional domain and the integral over the bounding super-surface S with the equation L (x, y, z, ...) = 0. If we adhere to the previous notation, then the formula has the form

However, Ostrogradsky did not use geometric images and terms that we use: the geometry of multidimensional spaces did not yet exist at that time.

In the Memoir on the Calculus of Variations of Multiple Integrals, two more important questions of the theory of such integrals are considered. First, Ostrogradskii deduces a formula for the change of variables in a multidimensional integral; second, for the first time he gives a complete and accurate description of the method for calculating an n-fold integral using n successive integrations over each of the variables within the appropriate limits. Finally, from the formulas contained in this memoir, it is easy to deduce general rule differentiation with respect to the parameter of a multidimensional integral, when not only the integrand but also the boundary of the region of integration depends on this parameter. This rule follows from the formulas present in the memoir in such a natural way that later mathematicians even identified it with one of the formulas of this memoir.

Ostrogradskii devoted a special work to the change of variables in multiple integrals. For a double integral, the corresponding rule was derived using formal transformations by Euler, for a triple integral, by Lagrange. However, although Lagrange's result is correct, his reasoning was not accurate: he seemed to proceed from the fact that the volume elements in the old and new variables - coordinates - are equal to each other. Ostrogradskii made a similar mistake in the just mentioned derivation of the rule for changing variables. In the article “On the transformation of variables in multiple integrals,” Ostrogradskiy disclosed Lagrange's error, and also for the first time presented that clear geometric method for transforming variables in a double integral, which, in a somewhat more rigorous form, is also presented in our manuals. Namely, when changing the variables in the integral according to the formulas, the region of integration is divided by the coordinate lines of the two systems u = const, v = const into infinitesimal curvilinear quadrangles. Then the integral can be obtained by first adding up those of its elements that correspond to an infinitely narrow curvilinear strip, and then, continuing to sum the elements by strips until they are all exhausted. A simple calculation gives for an area that can be regarded as a parallelogram up to a small higher order, the expression, where, is chosen so that the area is positive. As a result, we get the well-known formula

For a function of two variables defined as z = f(x, y) .

The double integral is written like this:

Here D- a flat figure bounded by lines, the expressions of which (equalities) are given in the task of calculating the double integral. Left and right - equalities in which the variable on the left x, and above and below - equalities in which the variable on the left is y... This place and further - one of the most important for understanding the technique of calculating the double integral.

Calculate double integral - means to find a number equal to the area of ​​the mentioned figure D .

Until we touch definitions of double integral , but we will learn to calculate it. It is easier to understand what a double integral is when you have solved several problems to calculate it, so you will find the definition of a double integral at the end of this lesson. Running a little ahead, we can only note that the definition of a double integral is also related to the aforementioned figure D .

If the figure D is a rectangle, all lines bounding it are straight lines. If the figure D- is curvilinear, then on the left and on the right it is bounded by straight lines, and above and below - by curved lines given by the equalities given in the assignment. There are times when the figure D- a triangle, but about such cases a little further.

To calculate the double integral, it is necessary, therefore, to sort the lines bordering the figure D, which has a strict name - the area of ​​integration. Sort into left and right and top and bottom. This will be required when reducing the double integral to the iterated integral - the method for calculating the double integral.

Rectangular area case:

Curved region case:

And this is already the solution of certain integrals familiar to us, in which the upper and lower limits of integration are given. Expressions that define the lines that bound the shape D, will be the limits of integration for ordinary definite integrals, to which we are already approaching.

Reduction of a Double Integral to a Repeated Integral

Rectangular area case

Let such a function have a double integral

To calculate this double integral , it is necessary to reduce it to a repeated integral, which has the form

.

First you need to calculate the inner (right) definite integral, then - the outer (left) definite integral.

You can change roles x and y

.

Example 1. Calculate double integral

We calculate the inner (right) integral, assuming that y is a constant. We receive.

.

Example 2. Calculate double integral

,

Solution. Reduce this double integral to the iterated integral

In the drawing, we build the area of ​​integration:

Now we calculate the outer (left) integral of the just calculated inner (right) integral:

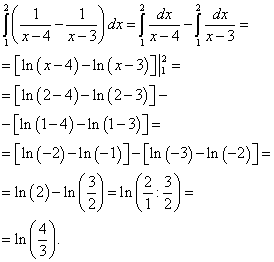
The result will be the solution to this double integral.

Calculate the double integral yourself and then see the solution

The case of a curved or triangular region

Let again be given a function of two variables f(x, y) , and the restrictions for D: already of a slightly different kind:

This entry means that the figure D left and right bound, as in the case of a rectilinear region - straight lines x = a and x = b, but below and above are curves that are given by equations and. In other words, and are functions.

Let such a function also have a double integral

To calculate this double integral, it is necessary to reduce it to a repeated integral, which has the form

.

Here the limits of integration a and b are numbers, and and are functions. In the case of a triangular region, one of the functions or is the equation of a straight line. This case will be analyzed in Example 3.

As in the case of a rectilinear region, you first need to calculate the right definite integral, then the left definite integral.

Likewise, you can swap roles x and y... Then the iterated integral will have the form

.

Such a repeated integral must be solved in the same way: first, the inner (right) integral, then the outer (left) integral.

Example 5. Calculate double integral

,

Solution. Reduce this double integral to the iterated integral

.

In the drawing, we build the integration area and see that it is triangular:

We calculate the inner (right) integral, considering x a constant. We receive.

Now we calculate the outer (left) integral of the just calculated inner (right) integral. First, we represent this integral as a sum of integrals:

.

We calculate the first term:

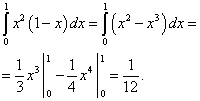
We calculate the second term:

We calculate the third term:

We get the sum, which will be the solution of this double integral:

.

Example 6. Calculate double integral

Solution. Reduce this double integral to the iterated integral

In the drawing, we build the area of ​​integration:

We calculate the inner (right) integral, considering x a constant. We receive.

.

Now we calculate the outer (left) integral of the just calculated inner (right) integral:

The result will be the solution to this double integral.

x- correct and incorrect, y- correct and incorrect domains of integration

It happens that the region of integration of a double integral is limited by such lines that it becomes necessary to split the region of integration into parts and solve each corresponding iterated integral separately. These are the cases when:

1) the area of ​​integration is a figure having two or more straight or curved lines in the form of a lower or upper (left or right) border;

2) the region of integration is a figure, the border of which the straight lines intersect at more than two points.

If the above applies to the left or right border of the region of integration, that is, the constraints set by the lines expressed in terms of x, then the region of integration is called x-wrong. If the straight y = y0 intersects the corresponding boundary at only one point, and if only one straight line or curve serves as the boundary, then the region of integration is called x- correct

Similarly, if the border defined by the lines expressed through y, straight x = x0 intersects at more than one point or if more than one straight line or curve serves as the boundary, then the region of integration is called y-wrong. Display the signs now y-the correct area, presumably, is quite simple.

So far, we have looked at examples with x- incorrect and y- correct areas of integration. Now let's consider the cases when the correctness condition is violated.

Example 7. Calculate the double integral, the integration area of ​​which is bounded by lines y = x , xy = 1 , y = 2 .

Solution. The area of ​​integration is y-wrong, since its lower boundary cannot be set with a single line y = y(x) ... As you can see in the picture above, the lower border is made up of y = x(dark burgundy) and xy= 1 (green). Therefore direct x= 1 (black) we can divide the region of integration into two parts - and.

This double integral is calculated as follows:

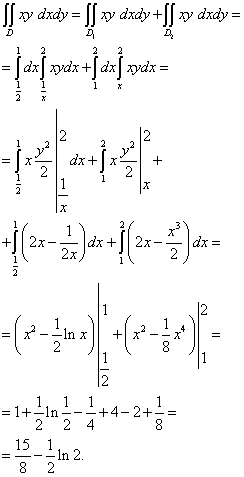
Changing the order of integration

As noted above, after reducing the double integral to the iterated integral, one can change the variables x and y roles, or, in other words, change the order of integration.

The change in the order of integration can be figuratively described by the following words About "Henry:" This is how a jungle dweller behaves - a beast, once in a cage, and this is how a cage dweller behaves - a man, lost in the jungle of doubts. " and the same: "Chalmers tore the letter into a thousand smallest pieces and began to tear his expensive carpet, pacing back and forth on it." ( O.Henry. Scheherazade of Madison Square.)

Then, if we have the left integral with respect to the variable x, and the right one - by y, then after changing the order of integration everything will be the other way around. Then the limits of integration for the "new" game should be "borrowed" from the "old" x, and the limits of integration for the "new" x should be obtained in the form inverse function, having solved the equation for x, which set the limit for the game.

Example 8.

.

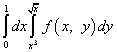Solution. After changing the order of integration, the integral over the game becomes left, and the integral over x becomes right. The limits of integration for the "new" game will be borrowed from the "old" x, that is, the lower limit is equal to zero, and the upper limit is equal to one. The limits of integration for the "old" game are given by equations and. Having solved these equations for x, we obtain new limits of integration for x:

(bottom) and (top).

Thus, after changing the order of integration, the repeated integral will be written as follows:

.

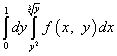After changing the order of integration in the double integral, the integration region often turns into y-wrong or x- incorrect (see the previous paragraph). Then it is required to split the region of integration into parts and solve each corresponding iterated integral separately.

Since splitting the integration domain into parts presents certain difficulties for many students, we will not limit ourselves to the example given in the previous paragraph, but consider a couple more examples.

Example 9. Change the order of integration for a re-integral

.

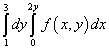Solution. So, the region of integration of this iterated integral is bounded by the straight lines y = 1 , y = 3 , x = 0 , x = 2y .

When integrating in a different order, the lower boundary of the region consists of two straight lines: AB and BC which are given by the equations y= 1 and y = x/ 2, which can be seen in the figure below.

The way out of this uncertainty is to split the integration region into two parts. The integration area will be divided by a straight line BM... We calculate the new limits of integration by finding the inverse function. According to this solution, the iterated integral after changing the order of integration will be equal to the sum of two integrals:

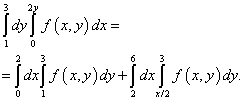
Naturally, the same will be the solution of the double integral, which reduces to the iterated integral given in the condition of this example.

Example 10. Change the order of integration for a re-integral

.

Solution. So, the region of integration of the iterated integral is bounded by the straight lines x = 0 , x= 2 and curves and.

As seen in the picture below, a straight line parallel to the axis 0x, will cross the lower boundary of the integration region at more than two points.

Therefore, we will divide the region of integration into three parts by straight lines, which are drawn in black in the figure. We calculate the new limits of integration by finding the inverse function. The limits for the three new areas of integration will be as follows.

According to this solution, the iterated integral after changing the order of integration will be equal to the sum of three integrals:

The same sum of three integrals will be equal to the double integral, which reduces to the iterated integral given in the condition of this example.

And yet, force majeure circumstances often interfere with students already at the previous step - setting the limits of integration. Anxiety and confusion are not without some reason: if it is usually enough to look at the drawing to break the integration region into parts, and to solve the repeated integral - the table of integrals, then some training experience is needed in setting the integration limits. Let us run through an example in which we will focus only on the arrangement of the limits of integration and, almost automatically, on the partition of the domain and omit the solution itself.

Example 11. Find the limits of integration of a double integral if the region of integration D is set as follows:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Solution. Explicitly (through x and y"without impurities"), the lines bounding the region of integration are not specified. Since for the x, they most often turn out to be straight lines touching at one point the upper and lower boundaries expressed through the game, then we will go exactly along this path. Moreover, when changing the order of integration, we get an integration region with the same area. Let's solve the inequalities with respect to the game and get:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

We build the resulting lines in the drawing. The x-integration limits are indeed the lines x= 0 and x= 2. But the area of ​​integration turned out to be y-wrong, since its upper boundary cannot be set with a single line y = y(x) .

Download from Depositfiles

Lectures 5-6

Topic2. Multiple integrals.

Double integral.

Control questions.

1. Double integral, its geometric and physical meaning

2. Properties of the double integral.

3. Calculation of the double integral in Cartesian coordinates.

4. Change of variables in a double integral. Calculation of the double integral in polar coordinates.

Let the function z = f (x , y) is defined in a bounded closed region D plane. Let's break up the area D arbitrarily on n elementary closed regions  1 , … , n with areas   1 , …,   n and diameters d 1 , …, d n respectively. We denote d the largest of the diameters of the regions  1 , … ,  n... In every area  k choose an arbitrary point P k (x k , y k) and compose integral sum function f(x, y)

S =
(1)

Definition. Double integral function f(x, y) by region D is called the limit of the integral sum

, (2)

if it exists.

Comment. Integral sum S depends on how the region is partitioned D and point selection P k (k=1, …, n). However, the limit
, if it exists, does not depend on the method of partitioning the region D and point selection P k .

A sufficient condition for the existence of a double integral. Double integral (1) exists if the function f(x, y) continuous in D except for a finite number of piecewise smooth curves and is bounded in D... In what follows, we will assume that all double integrals under consideration exist.

The geometric meaning of the double integral.

If f(x, y) ≥0 in the area D, then the double integral (1) is equal to the volume of the "cylindrical" body shown in the figure:

V =
(3)

A cylindrical body is bounded from below by an area D, from above  part of the surface z = f (x , y), from the sides  vertical line segments connecting the boundaries of this surface and the region D.

The physical meaning of the double integral. Flat plate mass.

Let a flat plate be given D with the known density function γ ( NS,at), then splitting the plate D into parts D i and choosing arbitrary points
, we obtain for the plate mass
, or, comparing with formula (2):

(4)

4. Some properties of the double integral.

Linearity. If WITH Is a numeric constant, then

Additivity. If the area D "Split" into areas D 1 and D 2, then

3) Area of ​​limited area D is equal to

(5)

Calculation of the double integral in Cartesian coordinates.

Let the region be given

Picture 1

D = { (x , y ): a ≤ x ≤ b , φ 1 (x ) ≤ y≤ φ 2 (x ) } (6)

Region D enclosed in a strip between straight lines x = a , y = b, from below and from above is bounded, respectively, by the curves y = φ 1 (x ) and y = φ 2 (x ) .

Double integral (1) over the area D(4) is calculated by passing to the iterated integral:

(7)

This iterated integral is calculated as follows. First, the internal integral is calculated

by variable y, wherein x is considered constant. The result is a function of the variable x, and then the "outer" integral of this function with respect to the variable is calculated x .

Comment. The process of passing to the iterated integral according to formula (7) is often called the arrangement of the limits of integration in the double integral. When setting the limits of integration, two points should be kept in mind. Firstly, the lower limit of integration should not exceed the upper one, and secondly, the limits of the external integral should be constant, and the internal integral should generally depend on the variable of integration of the external integral.

Now let the region D has the form

D = { (x , y ) : c ≤ y ≤ d , ψ 1 (y ) ≤ x ≤ ψ 2 (y ) } . (8)

Then

. (9)

Suppose that the area D can be represented in the form (6) and (8) simultaneously. Then the equality

(10)

The passage from one iterated integral to another in equality (10) is called changing the order of integration in the double integral.

Examples.

1) Change the order of integration in the integral

Solution. From the form of the iterated integral, we find the region

D = { (x , y ): 0 ≤ x ≤ 1, 2 x ≤ y≤ 2 } .

Let's draw the area D... From the figure, we see that this area is located in a horizontal strip between the straight lines y =0, y= 2 and between the lines x =0 and x= D

Sometimes variables are changed to simplify calculations:

,
(11)

If functions (11) are continuously differentiable and the determinant (Jacobian) is nonzero in the considered domain:

(12)

Ministry of Education and Science of the Russian Federation

Course work

Discipline: Higher Mathematics

(Basic Linear Programming)

On the topic: MULTIPLE INTEGRALS

Completed: ______________

Teacher:___________

Date ___________________

Grade _________________

Signature ________________

VORONEZH 2008

1 Multiple integrals

1.1 Double integral

1.2 Triple integral

1.3 Multiple integrals in curvilinear coordinates

1.4 Geometric and physical applications of multiple integrals

2 Curvilinear and surface integrals

2.1 Curvilinear integrals

2.2 Surface integrals

2.3 Geometric and physical applications

Bibliography

1 Multiple integrals

1.1 Double integral

Consider in the Oxy plane a closed region D bounded by a line L. We divide this region by some lines into n parts

, and the corresponding largest distances between points in each of these parts will be denoted by d 1, d 2, ..., d n. Let's choose point Р i in each part.

Let the function z = f (x, y) be given in the domain D. Let us denote by f (P 1), f (P 2),…, f (P n) the values ​​of this function at the selected points and compose the sum of products of the form f (P i) ΔS i:

, (1)

called the integral sum for the function f (x, y) in the domain D.

If the same limit of integral sums (1) exists for

and, which does not depend either on the method of partitioning the domain D into parts, or on the choice of points P i in them, then it is called the double integral of the function f (x, y) over the domain D and is denoted . (2)

Calculation of the double integral over the area D bounded by lines

x = a, x = b (a< b), где φ 1 (х) и φ 2 (х) непрерывны на (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла: = (3)

1.2 Triple integral

The concept of a triple integral is introduced by analogy with a double integral.

Let some domain V be given in space bounded by a closed surface S. Let us define a continuous function f (x, y, z) in this closed domain. Then we divide the region V into arbitrary parts Δv i, assuming the volume of each part to be equal to Δv i, and compose an integral sum of the form

, (4)

Limit at

integral sums (11), which does not depend on the method of partitioning the domain V and the choice of points P i in each subdomain of this domain, is called the triple integral of the function f (x, y, z) over the domain V: . (5)

The triple integral of the function f (x, y, z) over the region V is equal to the threefold integral over the same region:

. (6)

1.3 Multiple integrals in curvilinear coordinates

Let us introduce curvilinear coordinates on the plane, called polar coordinates. Let us choose point O (pole) and a ray emerging from it (polar axis).

Rice. Fig. 2 3

The coordinates of the point M (Fig. 2) will be the length of the MO segment - the polar radius ρ and the angle φ between the MO and the polar axis: M (ρ, φ). Note that for all points of the plane, except for the pole, ρ> 0, and the polar angle φ will be considered positive when measured in the counterclockwise direction and negative when measured in the opposite direction.

The relationship between the polar and Cartesian coordinates of the point M can be set by aligning the origin of the Cartesian coordinate system with the pole, and the positive semiaxis Ox - with the polar axis (Fig. 3). Then x = ρcosφ, у = ρsinφ. From here

, tg.

In the domain D bounded by the curves ρ = Φ 1 (φ) and ρ = Φ 2 (φ), where φ 1< φ < φ 2 , непрерывную функцию z = f(φ, ρ) (рис. 4).

(7)

In three-dimensional space, cylindrical and spherical coordinates are entered.

The cylindrical coordinates of the point P (ρ, φ, z) are the polar coordinates ρ, φ of the projection of this point on the plane Oxy and the applicate of this point z (Fig. 5).

Fig. 5 Fig. 6

Formulas for the transition from cylindrical coordinates to Cartesian coordinates can be specified as follows:

x = ρcosφ, y = ρsinφ, z = z. (eight)

In spherical coordinates, the position of a point in space is determined by the linear coordinate r - the distance from the point to the origin of the Cartesian coordinate system (or the pole of the spherical system), φ - the polar angle between the positive semiaxis Ox and the projection of the point onto the plane Oxy, and θ - the angle between the positive semiaxis of the axis Оz and segment OP (Fig. 6). Wherein

Let us set the formulas for the transition from spherical coordinates to Cartesian coordinates:

x = rsinθcosφ, y = rsinθsinφ, z = rcosθ. (nine)

Then the formulas for the transition to cylindrical or spherical coordinates in the triple integral will look like this:

, (10)

where F 1 and F 2 are functions obtained by substituting into the function f instead of x, y, z their expressions in terms of cylindrical (8) or spherical (9) coordinates.

1.4 Geometric and physical applications of multiple integrals

1) The area of ​​the flat area S:

(11)

Example 1.

Find the area of ​​a shape D bounded by lines

It is convenient to calculate this area by counting at the external variable. Then the boundaries of the region are given by the equations

and
is calculated using integration by parts: