Изследване на трептенията на нишковидното махало и измерване. Лабораторна работа по физика "изучаване на законите на математическо махало"

Лабораторна работа

Изучаване на законите на математическо махало

Обективен: Изучете законите на математическото махало и определете ускорението на гравитацията

Оборудване: Махало (топка на окачване), владетел, хронометър или часовник с втора ръка.

Кратка теория:

Математическото махало е осцилатор, което представлява механична система, състояща се от материална точка, разположена върху безтегловна неразтежима нишка или върху безтеглов прът в еднородно поле на гравитационните сили.

Дължината на махалото l е разстоянието от точката на окачване до центъра на тежестта на топката.

За практическо изчисление на периода на трептения използвайте формулата:

,

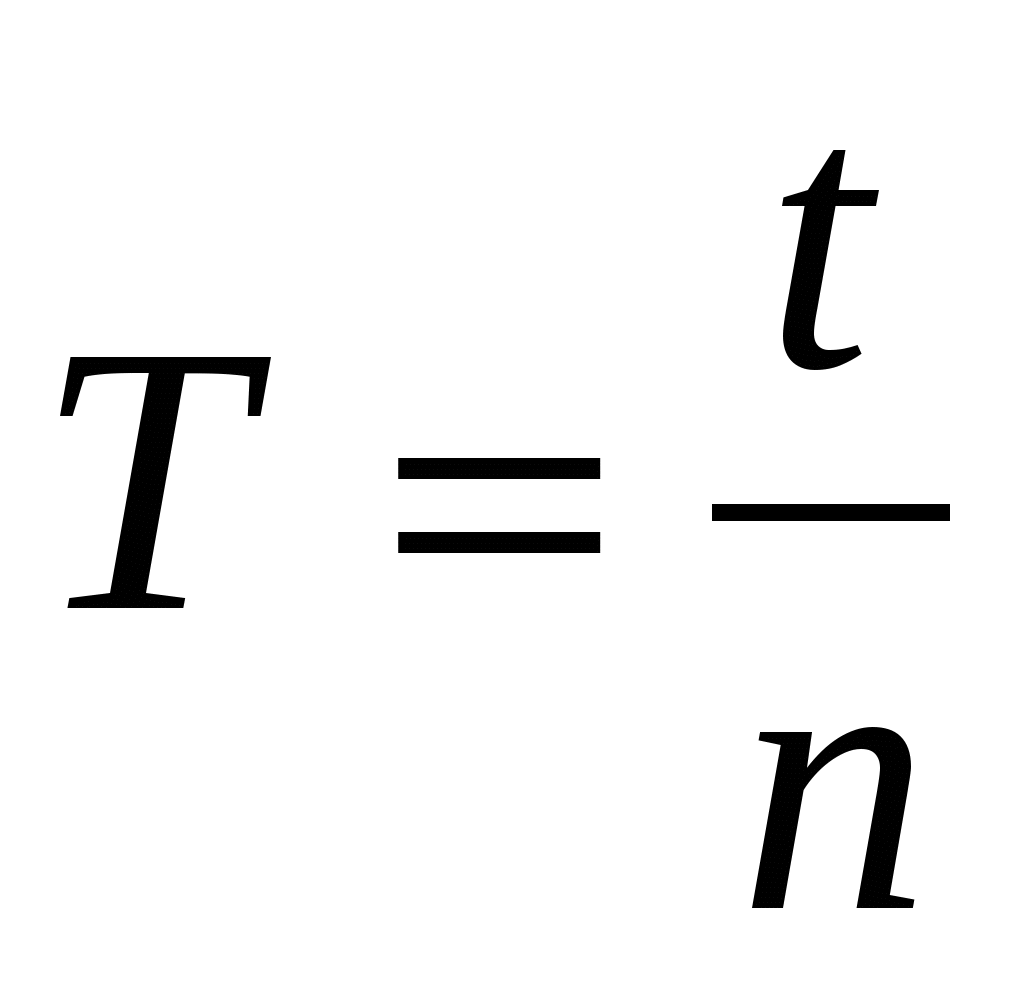където T е периодът на трептене,

t - време на трептене,

n е броят на пълните вибрации.

Съгласно законите на трептене периодът на махалото може да се определи по формулата:

,

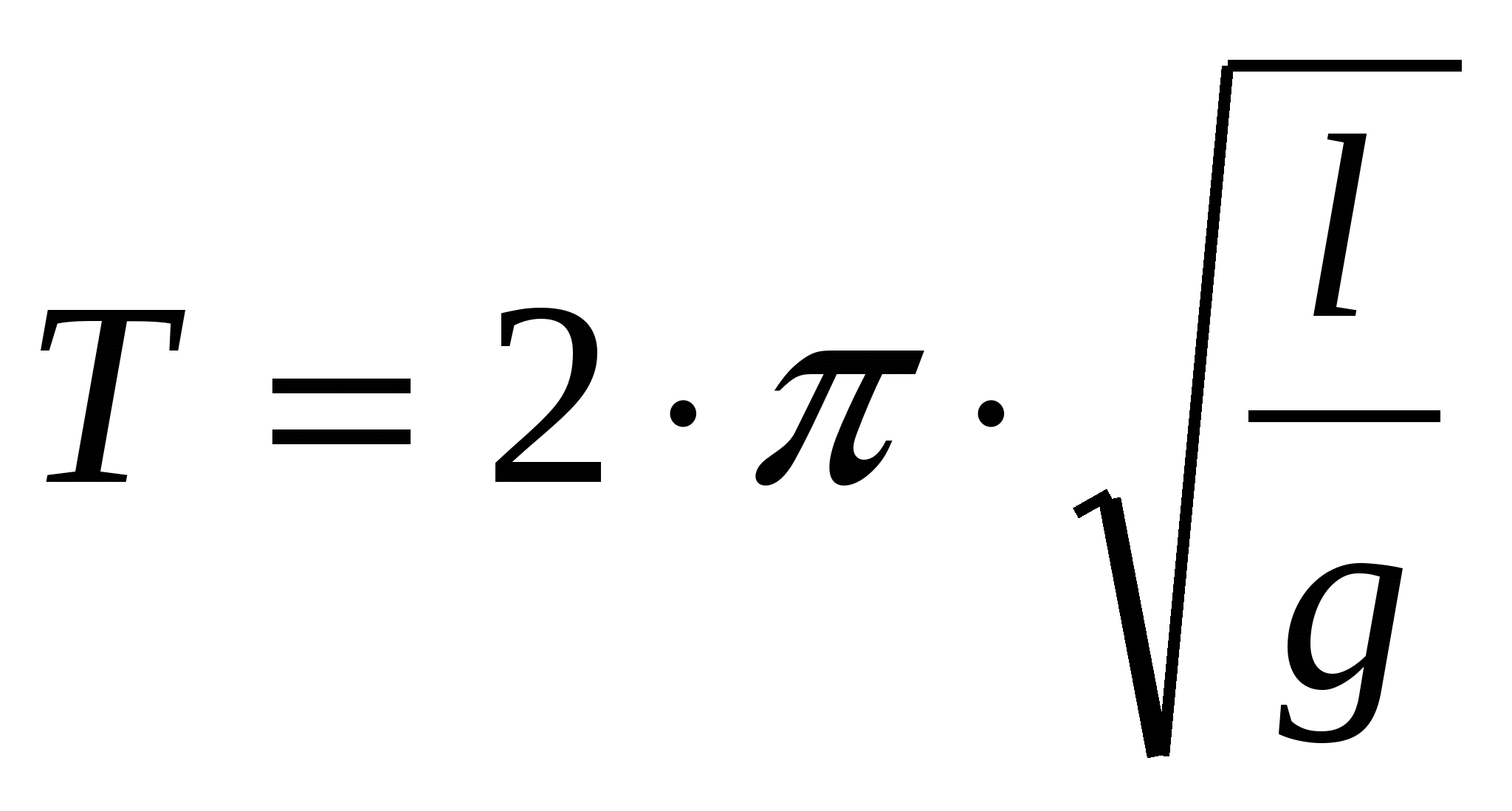Периодът на трептене на математическо махало не зависи от масата на топката.

P периодът на трептене на математическо махало е право пропорционален на дължината на махалото и обратно пропорционален на ускорението на гравитацията. Това уравнение се нарича формула на Хюйгенс.

Справка за историята

Кристиан Хюйгенс ван Цуйлих (14 април 1629 - 8 юли 1695). Холандски физик, математик, механик и астроном и изобретател. Роден в Хага. Учи право в университета в Лайден, но не спира да учи математика. Въз основа на изследванията на Галилей той решава редица проблеми в механиката. През 1656 г., на 27-годишна възраст, той проектира първия часовник за евакуационно махало. Създаването на часовник, който измерва времето с безпрецедентна за това време точност, е имало далечни последици за развитието на физическия експеримент и практическата дейност на човека. Преди това, в края на краищата, времето се измерваше чрез изтичане на вода, изгаряне на факла или свещ. Теорията за трептенията, създадена от Хюйгенс към 1673 г., е една от основите за по-късното разбиране на природата на светлината.

От формулата на Хюйгенс, чрез математически преобразувания, получаваме израз за ускорението на гравитацията:

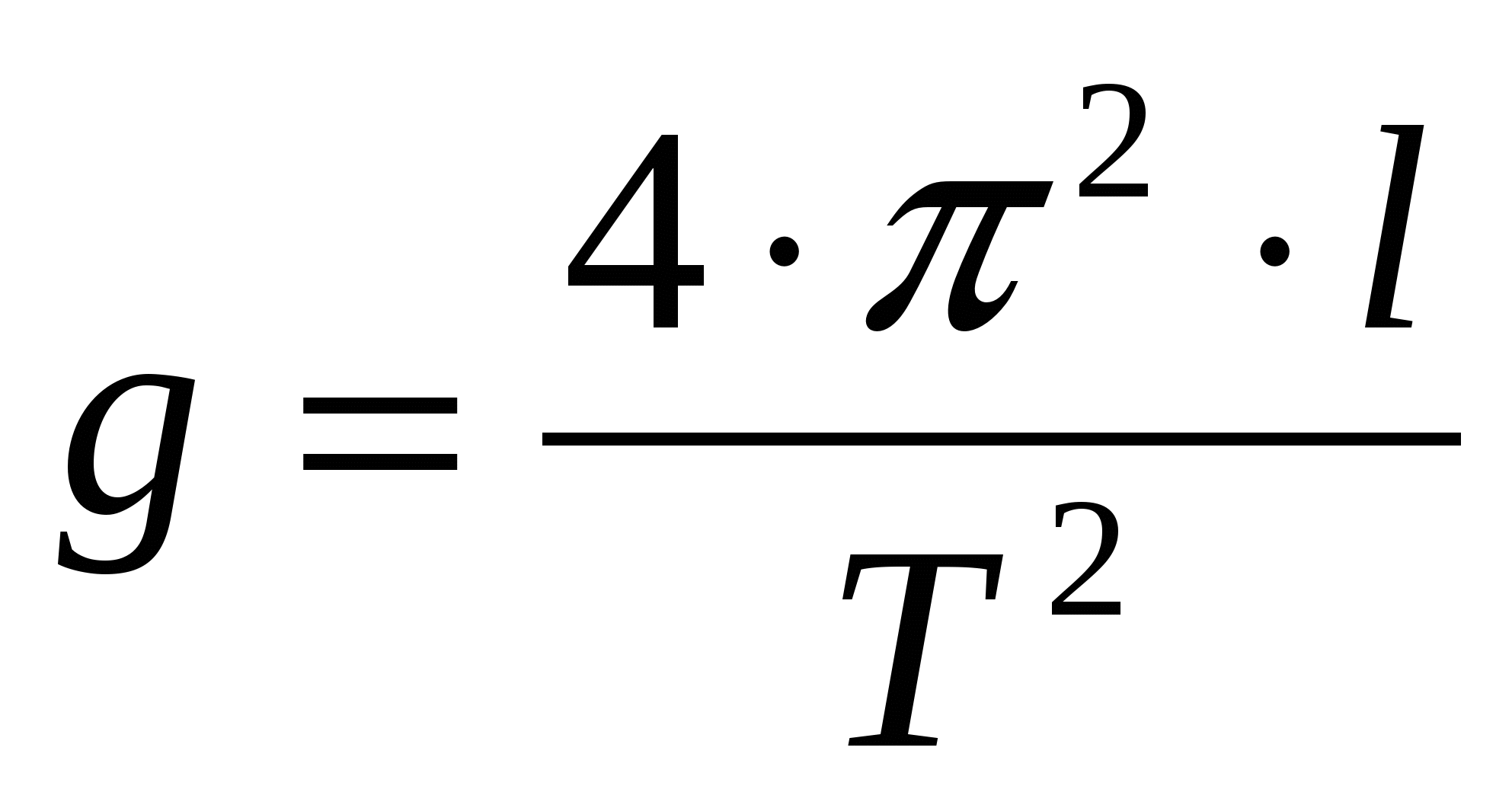
Истински модел на математическо махало в нашите експерименти ще бъде малка топка, окачена на тънка еластична нишка. Размерът на топката трябва да бъде малък в сравнение с дължината на конеца. Това дава възможност да се приеме, че цялата маса е концентрирана в една точка, в центъра на тежестта на топката.

Работен процес:

Определете цената на разделяне на устройствата:

владетел ...... ..m / div.

хронометър …… .s / div.

2. Определете грешката на инструментите (абсолютната грешка на инструментите е равна на interval скалния интервал):

владетел Δ л = …… ..м

хронометър Δ т \u003d …… .s

Задайте максималната дължина на махалото и го измерете л 1 \u003d… .m.

Стартирайте махалото (ъгъл на отклонение 10-15 0) и навреме т пребройте броя на вибрациите н (поне 7).

Като промените броя на вибрациите, повторете експеримента още 3 пъти.

t 2 \u003d ………, n 2 \u003d …………. T 2 \u003d ………,

t 3 \u003d ………, n 3 \u003d …………. Т 3 \u003d ………,

t 4 \u003d ………, n 4 \u003d …………. T 4 \u003d ………,

Променете дължината на махалото л 2 \u003d… .m и повторете всички измервания.

Въведете данните в таблицата.

№ измервания

Дължина на махалото

л, m

№ опит

Време на трептене,

t, s

Броят на вибрациите

н

Период на трептене,

T, s

Средна стойност на периода, T avg, s

Ускорение на свободно падане, g, m / s 2.

Средна стойност

ускорение на свободно падане, g средно, m / s 2.

l cf \u003d

т Сряда \u003d

относително: абсолютно:

,

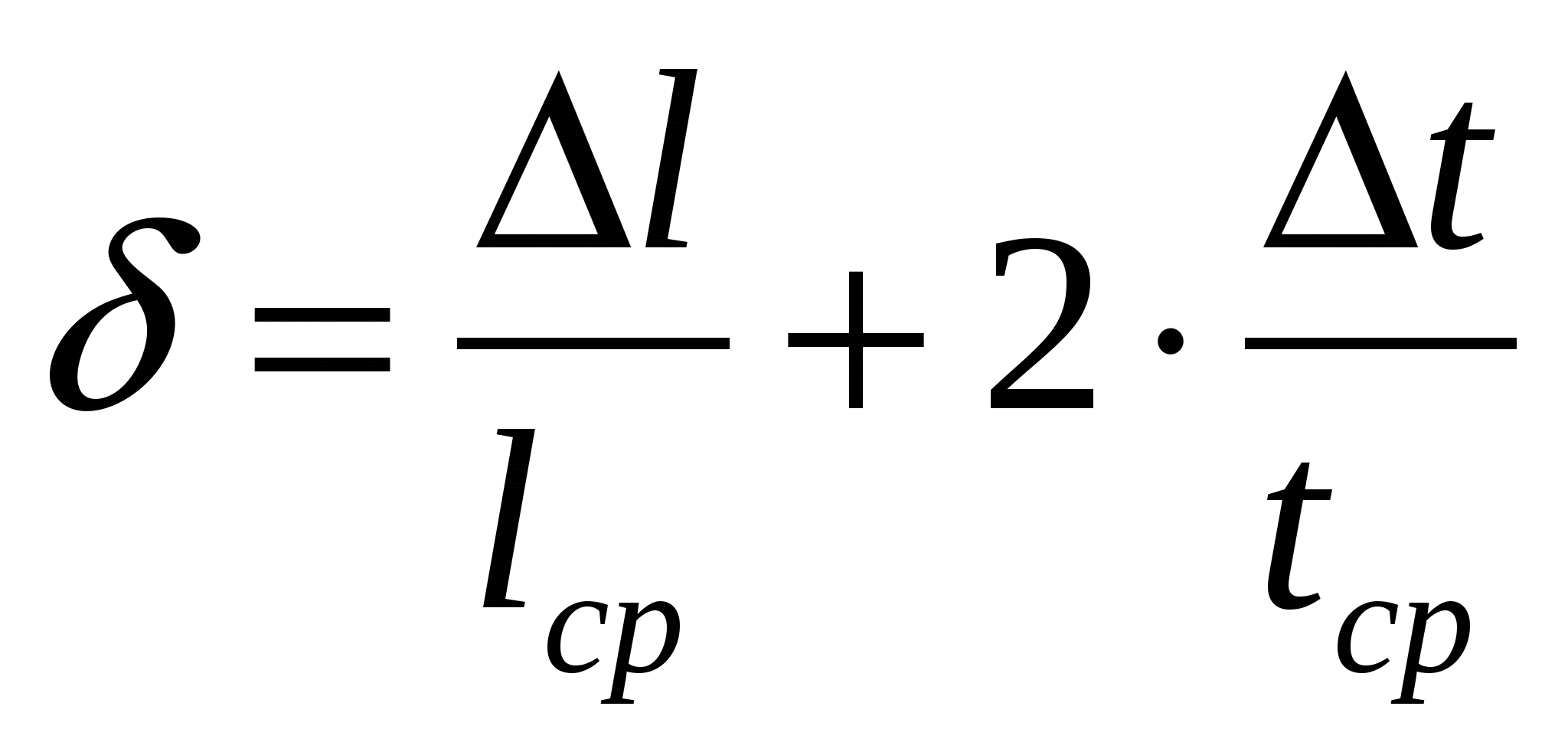
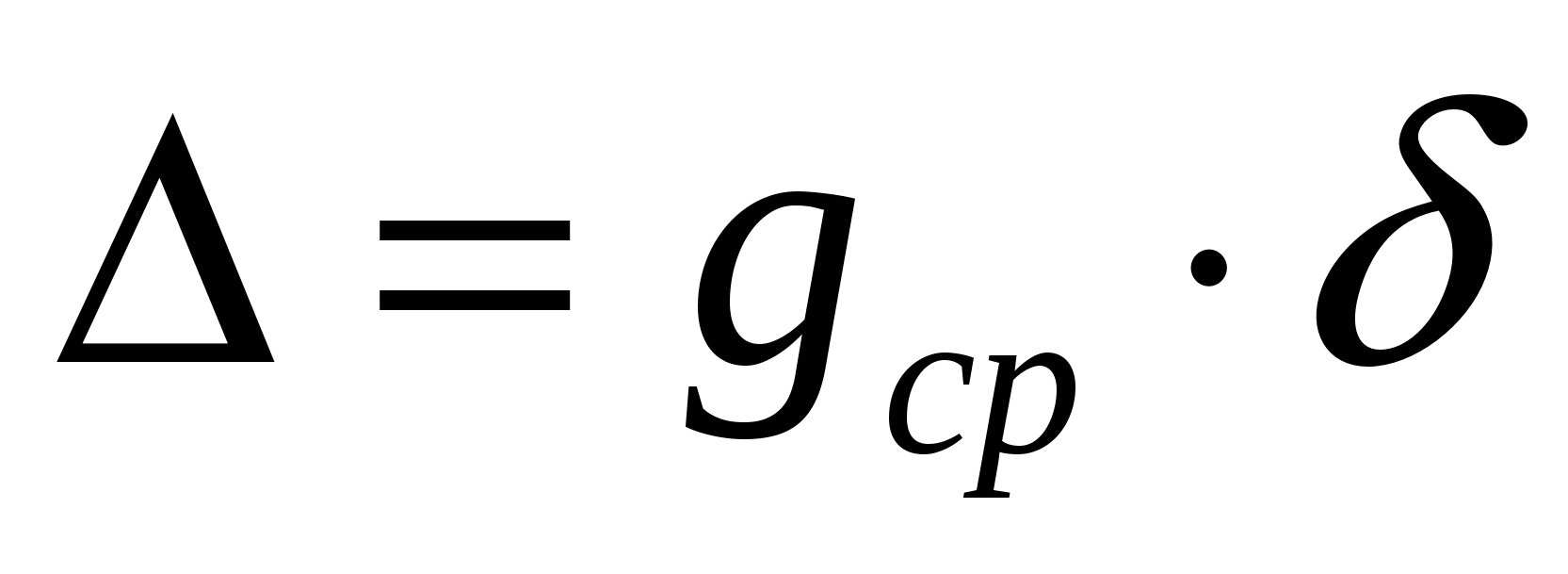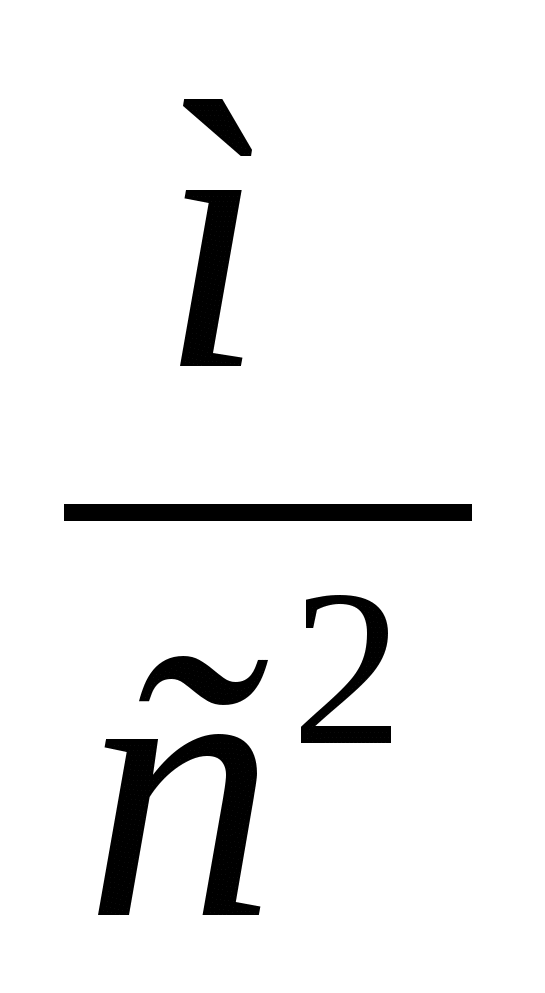
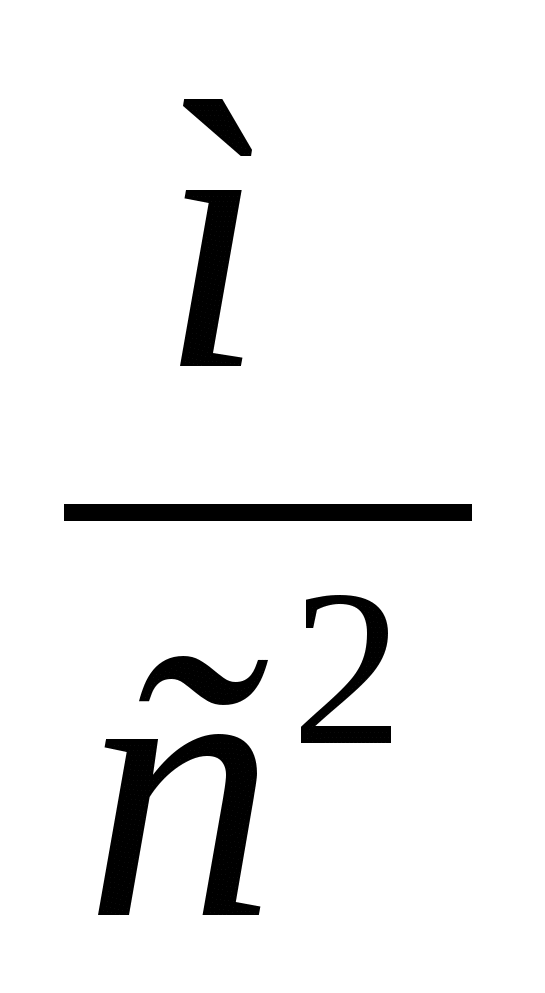
Контролни въпроси:

Колко време е математическото махало с период от 2 s?

Намерете масата на тежестта, която върху пружина с твърдост 250 N / m прави 20 вибрации за 16 s.

Ускорението на гравитацията на Луната е 1,7 m / s 2. Какъв ще бъде периодът на трептене на математическото махало на Луната, ако на Земята е равно на 1 s? Отговорът зависи ли от теглото на товара?

Координатата на трептящото тяло се променя съгласно закона x \u003d 0.5sin 45πt. Какви са амплитудата и периода на трептенията?

Амплитудата на непрекъснатите трептения на точката е 12 cm, линейната честота е 14 Hz, началната фаза на трептенията е 0. Напишете уравнението за движение на точката x \u003d x (t).

Разделяне на мащаба

Разлика (без оглед на знака) между стойностите физическо количествосъответстващи на ограничителното деление на скалата. В цифровите устройства стъпката на дискретност служи като характеристика, която замества стойността на разделяне на скалата.

а) изберете двете най-близки цифрови линии на скалата;

в) разликата в стойностите (извадете по-малкото от по-голямото) за избраните щрихи, разделете на броя на деленията.

З.

тази фигура показва термометър в голям мащаб. Ще го използваме, за да илюстрираме правилото за изчисляване на цената на разделяне.

а) изберете дигитализираните удари 20 ° С и 40 ° С

б) 10 разделения (пропуски) между тях

в) изчислете: (40 ° С - 20 ° С): 10 деления \u003d 2 ° С / дел.

Отговор: цената на деленията \u003d 2 ° С / дел,

Цифровите устройства нямат скала изрично и вместо цената на разделяне, те посочват цената на единицата от най-малко значимата цифра на числото при отчитане на устройството.

P


пример:

1) цената за разделяне на скалата на това устройство е 1 (условни единици) / дел.

2
) делението на скалата на това устройство е 0,01 (условни единици) / дел.

3
) делението на скалата на това устройство е 0,1 (конвенционални единици) / дел.

4) делението на скалата на това устройство е 0,001 (условни единици) / дел.

I. Обективен

Наблюдения на колебателните движения на математическо махало, реализирано на устройство, чиято функционална схема е показана на фигура 1.

Измерване на периода на трептене на махалото при различни дължини и амплитуди.

Определяне на режима на изохронизъм на трептенията на математическо махало.

Изчисляване на гравитационното ускорение на топката от резултатите от посочените измервания.

II ... Теоретична част

Помислете за устройство, състоящо се от малка топка, прикрепена към неподвижна точка на окачване с безтегловна неразтеглива резба с определена дължина (фиг. 1)

Ако размерът на топката е много по-малък от дължинатал конци, тогава топката може да се разглежда като материална точка; и ако масата на топката е много по-голяма от масата на конеца, тогава последната може да се счита за безтегловна. Конецът също може да се счита за неразтеглив, при условие че гравитацията на топката причинява безкрайно малко удължаване на конеца.

Това устройство ви позволява да симулирате трептене на движението на така нареченото математическо махало.

Фигура: 1. Устройство за изследване на трептенията на математическо махало: 1. Метална плоча за задаване на ъгъла на отклонение на махалото; 2. Подвижна платформа; 3. Линейка за измерване.

Фигура 2. Илюстрация на колебателните движения на математическо махало.

Всъщност в първоначалното състояние нишката е насочена вертикално надолу (позиция 1 на фигура 2). В този случай силатаF опън и якост на конецаmg тежестите на топката съвпадат с посоката на конеца, но противоположно насочени. Тъй като нишката е неразтеглива, и двете сили се уравновесяват, т.е.F \u003d mg ... Топката е в покой. Това състояние на махалото се нарича неговото равновесно положение.

Нека извадим махалото от равновесното му положение, като отклоним топката от първоначалното й състояние под ъгълφ 0 (фиг. 2). След това го пуснете, без да натискате. Чрез гравитацияmg топката ще започне да се движи към равновесното положение, след известно време ще я премине, след което от другата страна на равновесното положение ще се отклони от нея с някакъв ъгъл по-малък отφ 0 и под действието на гравитацията отново ще се втурне към равновесното положение. При липса на външни влияния върху топката, последната ще извърши описаното движение в една равнина. Очевидно траекторията на топката ще бъде кръгла дъга с радиусл ... Тези движения се наричат \u200b\u200bвибрации.

Поради действието на силата на съпротивлението върху топката, нейните трептения ще бъдат затихващи, което се доказва от факта, че след всяко преминаване на равновесие тя ще се отклонява от нея под все по-малък и по-малък ъгъл. Ако обаче този процес се наблюдава за сравнително кратко време, тогава трептящият процес може да бъде разпознат като непрекъснат.

Помислете за силите, които действат върху топката в произволно времет. Нека φ - ъгълът на отклонение на конеца в този момент. Пишем следното уравнение на втория закон на Нютон в посокаτ съвпада с допирателната, изтеглена към точката на траекторията на топката, в която се намира в разглеждания момент от времет.

ma τ \u003d - mg sin φ (1)

Тук a τ - тангенциално ускорение,м Е масата на топката. Знакът минус вдясно в (1) отчита факта, че при движение от равновесно положение нагоре, силата на гравитацията предотвратява това движение.

Ъгловото ускорение ε на топката се определя като второ производно на ъгъла по времеφ, т.е.

. (2)

Между тангенциалното ускорениеa τ и ъглова ε има очевидна връзка

(3)

Уравнение (1), отчитайки формули (2) и (3), има формата:

. (4)

В уравнение (4) неизвестната функцияφ (t) стои под знака на производното от втори ред. Такова уравнение в математиката се нарича обикновено диференциално уравнение от втори ред.

Тя може да бъде опростена, ако вземем предвид това под малки ъглиφ, измерено в радиани. Тогава вместо (4) ще имаме

. (5)

Уравнение (5) описва движението на махалото. Нарича се още уравнението на хармоничния осцилатор.

Чрез директно заместване може да се провери дали решението на уравнение (5) има формата

, (6)

ако обозначаваме с

. (7)

По този начин може да се види, че промените в ъгълаφ във времето се случва съгласно синусоидален закон. Количествотоφ 0 , равен на максималния ъгъл на отклонение от равновесното положение се нарича амплитуда на хармоничните вибрации. Величината на амплитудата в този случай зависи от първоначалното отклонение. Стойността под синусоида се нарича фаза. Фазата нараства пропорционално на времето. Стойността под синусоидалния знак се нарича начална фаза, която е нула в разглежданото движение.

Синусовата функция, която определя естеството на колебателните движения, е периодична функция с период, равен на. Последното означава, че ако следт обозначим периода на трептене на махалото, тогава можем да напишем следното равенство за стойността на фазата

, (8)

където е кръговата честота.

Сега като се вземе предвид (7) за периодаЩе имаме:

(9)

Отношение (9) показва, че линеаризацията на уравнение (4) е довела до уравнение (5), чието решение признава независимосттаT на амплитудата φ 0.

Такива колебания се наричат \u200b\u200bизохронни.

Формула (9) може да бъде представена както следва:

k l, (10)

откъде през

(11)

наклонът на линейната функционална зависимост на функциятаT 2 от аргумент l.

Следователно, изохронизмът на колебанията на махалото се проверява чрез валидността на съотношението (10) според измерените стойности на периодат при различни стойностил свързани със същия ъгълφ 0 .

Функционалната зависимост, изградена от експерименталните точки, позволява да се определи наклонътk, чрез числовата стойност на която ускорениетож свободното падане на топката се изчислява, както следва:

. (12)

Освен това, чрез единични измерванияT и l ускорение g може да се изчисли и от това съотношение:

(13)

III ... Процедура на експеримента

Тъй като линеаризацията на уравнение (4), довела до уравнение (5), което описва изохронни трептения, се основава на предположението, очевидно е, че изохронният обхват се определя от стойностите на ъгълаφ 0 при които има линейна зависимост.

Следователно, за да се определи диапазон от стойностиφ 0 , за което е валидна релацията (10), е необходимо за няколко стойностиφ 0 направете измервания, които ви позволяват да изграждате зависимости, след това от посочените функционални зависимости изчислете наклонак и за избраните ъглиφ 0 изчисляване на стойностиж съгласно (12) и ги сравнете с общоприетата стойностg \u003d 9,8 m / s 2. Тези ъгли φ 0 за които изчислената стойностж като се вземе предвид грешката при измерването, той ще запази същите числени стойности и ще определи диапазона на изохронизъм на трептенията, реализиран от това устройство.

Редът на измерванията е следният: избира се конкретна стойност на ъгълаφ 0 , с което е необходимо да се отклони топката от равновесно положение, задава се дължината на махалото, провежда се експеримент, през който се измерва периодътт ... Експериментът се извършва няколко пъти, така че под фиксиран ъгълφ 0 необходимо е да има от три до пет измерени стойностиl и T.

Това ще бъде първата серия от измервания в равнината (Т 2, л ) ще даде само една точка. За да проверите формула (10) под даден ъгълφ 0 трябва да бъдат произведени няколко такива партиди.

Предлага се да се направят пет такива серии измервания за всеки от ъглите.φ 0 , като които са избрани следните три ъгъла:φ 0 \u003d 10 около; φ 0 \u003d 20 около; φ 0 \u003d 30 о.

Множество измерени стойностиl и T за избрания ъгълφ 0 техните аритметични средни стойности се изчисляват по формулите:

, (14)

където n - брой измервания.

В резултат на измерванията ученикът трябва да попълни следните три таблици с експериментални данни и да ги покаже на учителя.

Маса 1.

φ 0 \u003d 10 о
измервателен номер	серия 1		серия 2		серия 3		серия 4		епизод 5

Таблица 2.

φ 0 \u003d 20 о
измервателен номер	серия 1		серия 2		серия 3		серия 4		епизод 5

Таблица 3.

φ 0 \u003d 30 о
измервателен номер	серия 1		серия 2		серия 3		серия 4		епизод 5

При измерване на дължинатал махалото трябва да се има предвид, че последното е съставено от дължината на конеца, задържащ топката, и радиуса на топката.

Радиусът на топката се изчислява чрез нейния диаметър, който се измерва с нониус. Тъй като топката не представлява перфектна сферична повърхност, всяко измерване на диаметъра ще даде стойност, която е малко по-различна от предварително измерената.

Устройството, което осъществява колебателните движения на махалото, има устройство, което регулира дължината на конеца. В този случай дължината на конеца може да бъде измерена по два начина: или да се приложи референтна резба към конеца с фиксирана дължина, чиято дължина след това трябва да бъде измерена на измервателна линийка; или вземете нишка с определена дължина като референтна нишка и фиксирайте дължината на нишката на махалото с помощта на регулируемо устройство на това устройство.

Подвижната платформа (виж фиг. 1) ви позволява да измерите дължината на махалото по друг начин. За да направите това, е необходимо да комбинирате нишката на махалото заедно с топката с горната равнина на подвижната платформа (вижте фиг. 3) Същата позиция на платформата може да бъде фиксирана върху измервателната линийка - това ще бъде дължината на конеца заедно с топката, от която трябва да се извади радиусът на топката. Диаметърът на топката трябва да се измерва с дебеломер.

Фигура: 3.

Период Т трептенията на махалото са най-добре дефинирани по следния начин: измерете времетот няколко трептения на махалото и след това разделете това време на броя на трептенията. Трябва да се има предвид, че времето на едно трептене означава времето, през което топката се връща от една от крайните позиции в същата позиция.

За да зададете необходимия ъгълφ 0 необходимо е да се използва правоъгълна метална плоча, върху която от една точка излизат няколко направляващи линии, наклонени под различни ъгли към вертикалната линия, излъчваща се от тази точка. Тези ъгли могат да се измерват с транспортир.

Подвижната платформа позволява на правоъгълната плоча да се подравни с точката на окачване на нишката на махалото, така че вертикалната линия на плочата да съвпада с нишката на махалото, когато топката е в долно положение.

След това подравняване подвижната платформа заедно с плочата може да бъде фиксирана. Сега, когато нишката е отклонена под един или друг ъгъл, тя трябва да бъде подравнена с една от линиите на плочата, която определя определен ъгъл (виж фиг. 1)

IV ... Обработка на резултатите от измерванията

Всяка от измерените стойностиl и T представени в таблици 1-3 не са точни стойности, тъй като те се измерват с определени грешки.

В такива случаи аритметичните средни стойности, изчислени по формули (14), се приемат като точни стойности на посочените величини. Тогава грешката на измерването ще означава модула на максималното отклонение на всички измерени стойности от средната им аритметична стойност. А именно грешката ∆1 измерванията на дължината на махалото ще бъдат определени като

∆ 1 \u003d макс. | l i - l cf |, (15)

и грешката ∆ 2 - периодът на трептене на махалото трябва да се изчисли, както следва:

∆ 2 \u003d макс | T i - T av | ... (16)

Във формули (15) - (16) индексътi \u003d 1,2,3… преминава през всички измервателни числа на съответните величини.

Ще обработим резултатите от измерването на компютър в програматаMicrosoft Excel и демонстрира технологията на необходимите изчисления на конкретни резултати от измерванията.

Нека Таблица 3 се попълни със следните действителни данни.

Таблица 3

φ 0 \u003d 30 о
измервателен номер	серия 1		серия 2		серия 3		серия 4		епизод 5
	0,505 0,495 0,503 0,498 0,500	1,434 1,434 1,428 1,422 1,418	0,606 0,594 0,603 0,597 0,600	1,547 1,553 1,557 1,575 1,553	0,704 0,696 0,702 0,698 0,700	1,685 1,681 1,678 1,691 1,687	0,806 0,794 0,804 0,797 0,800	1,807 1,815 1,791 1,791 1,800	0,904 0,896 0,903 0,898 0,900	1,907 1,909 1,925 1,906 1,897

За всяка серия от измервания е необходимо да се изчисляват с помощта на формули (14)l av и T av и след това изграждане на зависимостT cf 2 \u003d f (l cf) ... За удобство въвеждаме обозначението:T cf 2 \u003d y 1, l cf \u003d x 1.

Преди да пристъпим към посочените изчисления, ние конструираме в програматаExcel таблица 3 и подгответе формата на таблица 4, чиито данни ще бъдат използвани при конструиране на функционалната зависимостy 1 \u003d f (x 1).

В Excel Таблица 3 се формира, както следва.

На лист1 от работната книгаExcel активиране на набор от клетки клеткаA 1: A 2, обединете ги и въведете заглавието на първата колона в получената обединена клетка от клавиатурата: “н измервателен номер", Активирайте диапазона от клеткиB 1: C 1, обединете ги и въведете общата заглавка на втората и третата колона в получената обединена клетка от клавиатурата: „серия 1 ", Активирайте клеткатаБ. 2 и въведете от клавиатурата подзаглавието на втората колона на таблица 3: „л „След което активираме клетка C2 и въвеждаме в нея от клавиатурата подзаглавието на третата колона на Таблица 3:“т ". Нека повторим посочените действия за останалите колони от Таблица 3. В резултат на горните действия получаваме формата на Таблица 3.

Сега нека попълним получения формат с данните от таблица 3, в резултат на което получаваме таблица 3 в програматаExcel.

За изграждане на формата на таблица 4 в програматаExcel на Лист1 от работната книгаExcel активирайте клеткатаA 9 и въведете заглавката на първата колона в нея от клавиатурата: „п Б 9 и въведете заглавката на втората колона в него от клавиатурата: „l cf \u003d x 1 ". По същия начин въвеждаме от клавиатурата заглавията на третата, четвъртата и петата колона: „T cf "," T cf 2 \u003d y 1 "и" y 1 / x 1 "в клетки C 1, D 1 и E 1 съответно. След това активираме клеткатаA 10 и въведете числото 1 в него от клавиатурата, в клеткатаA 11 цифра 2, активирайте диапазона от клеткиA 10: A 11 и се довършва автоматично до клеткатаA 14. В резултат на изпълнението на горните действия получаваме таблица 4.

Таблица 4.

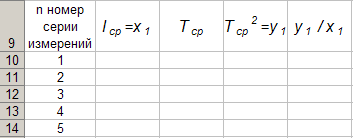
Ще демонстрираме технологията за запълване на първия ред от Таблица 4 чрез обработка на измервания от серия 1.

За което програмираме първата формула в (14), получавамеl Сряда и го поставете в таблица 4.Б. 10 и въведете от клавиатурата формулата "\u003d SUM (B3: B7) * (1/5)".

След това програмираме втората формула в (14).Е. 2 и въведете формулата "\u003d SUM (C3: C7) * (1/5)" от клавиатурата.

Получаваме T av и го квадрат, и след това изчислете съотношението. За да направите това, активирайте клеткатад 10 и въведете формулата "\u003d C10 ^ 2" от клавиатурата, след което активирайте клеткатаЕ. 10 и въведете формулата "\u003d D10 / B10" от клавиатурата. След всички тези действия първият ред на таблица 4 приема формата

След повторение на тези изчисления за други серии, Таблица 4 приема окончателната форма

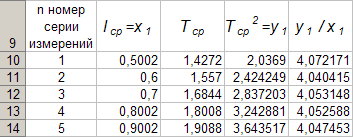
Данните в таблица 4 позволяват използването на програматаExcel изграждане на графика на функционалната зависимостy 1 \u003d f (x 1).

За да направите това, активирайте диапазона от клеткиD 10: D 14, нека се обадим на съветника за програмни функцииExcel , изберете типа диаграма "Scatter", първия изглед. Преместете курсора на мишката до бутона „Напред“ и изпълнете едно щракване на левия бутон на мишката (LMB). След това отидете в раздела Ред. За да направите това, преместете курсора на мишката в раздела "Ред", разположен в горната част на прозореца "Съветник за диаграми" и изпълнете едно щракване с LMB. След това поставете курсора в полето "X Стойности" и след това преместете курсора на мишката в клеткатаБ. 10, натиснете LMB и без да го пускате, преместете курсора на мишката до клеткатаБ. 14 и след това освободете LMB. В резултат на това формулата „\u003d Sheet1! $B $ 10: $ B $ 14 ". Сега преместете курсора на мишката до бутона „Напред“ и изпълнете два LMB щраквания подред, след това преместете курсора на мишката до бутона „Finish“ и изпълнете едно щракване с LMB. На лист1 от работната книгаExcel ще се появи графика на функционалната зависимостy 1 \u003d f (x 1) ... Активираме ред 10 и добавяме нов ред, след което влизаме от клавиатурата в клеткитеA 10: E 10 цифри "0". След това преместете курсора на мишката до която и да е точка на диаграмата и изпълнете едно щракване с LMB. Нека да увеличим диапазона от данни на диаграмата, за който преместваме курсора на мишката до границата на диапазона от стойностиy 1 и преместете маркера, разположен в горния десен ъгъл на границата, до клеткатад 10. Нека направим същото с обхватаx 1.

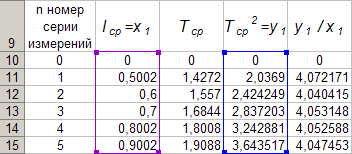
Сега преместете курсора на мишката до която и да е точка на графиката и изпълнете едно щракване с десен бутон (RMB). В контекстното меню, което се показва, преместете курсора на мишката към командата „Добавяне на линия на тенденция“ и изпълнете едно щракване с LMB. Фигура 4 илюстрира резултата от тези конструкции.

Фигура 4.

Фигура 4 показва, че зависимосттаy 1 \u003d f (x 1) е линейна и се описва от уравнението

y 1 \u003d 4,04 8 x 1 + 0,00 24 (17)

Уравнение 17 показва, че наклонътк от уравнение (10) е равно на:к \u003d 4,0493. Ако тази стойностк заместен във формула (12), тогава получаваме стойността на ускорението на гравитацията.

Наклонк в уравнение (10) може да се изчисли от данните в таблица 4 по формулата

(18)

За да направите това, активирайте клеткатаA 17 и въведете формулата „\u003d SUM (E 11: E 15) * (1/5) "

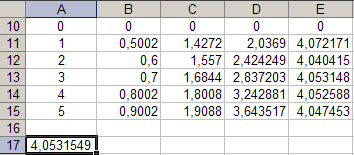
получаваме k \u003d 4,053, т.е. число, близко до числок получено от графиката, показана на фигура 4.

Очевидно е, че числото, получено по формула (12), използващо количествоток от уравнение (17) ще има известна грешка.

За да изчислим тази грешка, нека се върнем към данните в таблици 3 и 4.

Първо в програматаExcel създайте нов формат на таблица 5. Защо на Sheet1 на работната книгаExcel активирайте клеткатаA 19 и въведете заглавката на първата колона в нея от клавиатурата: „н измерване на сериен номер ", активирайте клеткатаБ. 19 и въведете заглавието на втората колона в него от клавиатурата: „∆1 съгласно (15) ". По същия начин въведете заглавките на третата колона от клавиатурата: „∆2 до (16) "в клетка C 19. След това активирайте клеткатаA 20 и въведете числото 1 в него от клавиатурата, в клеткатаA 21 цифра 2, активирайте диапазона от клеткиA 20: A 21 и се довършва автоматично до клеткатаA 26. В резултат на изпълнението на горните действия получаваме таблица 5.

Таблица 5.

При програмиране на формули (15) и (16) е необходимоl i и T i , вземете всяка серия от измервания от таблица 3 иl av и T av от данните в таблица 4.

За да се изчисли ∆1 за първата серия от измервания е необходимо да се активира клеткатаМ 3 и въведете формулата “\u003d ABS (B3-B $ 11))” в нея от клавиатурата, след което ще се довършим автоматично до клеткатаМ 7. Сега в клеткатаБ. 20 ще въведем от клавиатурата формулата "\u003d MAX (M3: M7)".

За да се изчисли ∆2 според данните от същата серия е необходимо да се активира клеткатан 3 и въведете формулата "\u003d ABS (C3-C $ 11)" в нея от клавиатурата, след което ще се довършим автоматично до клеткатан 7. Сега в клетката° С 20 ще въведем от клавиатурата формулата "\u003d MAX (N3: N7)".

В резултат на това Таблица 5 приема формата

След извършване на изчисления съгласно (15) и (16) за данни от други серии от измервания, Таблица 5 приема формата

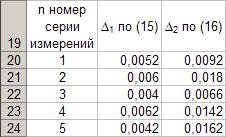
От данните в таблица 5 е очевидно, че за всяка серия от измервания, точните стойности на дължинатал махало и периодт трептенията на махалото се определят като

l \u003d l av ± ∆ 1, T \u003d T av ± ∆ 2 (19)

Освен това се оказва, че ∆1 и ∆ 2 са различни за всяка от дължините на махалото. От формули (19) следва, че правата линия на фиг. 4 е изчертана с грешка и в близост до нея има така наречения разпръскване на експериментални данни.

За да вземем предвид разсейването на експериментални данни, нека изчислим още две функционални зависимости:

(T av + ∆ 2) 2 \u003d f (l av + ∆ 1), (20)

(T av - ∆ 2) 2 \u003d f (l av - ∆ 1). (21)

За да изчислим зависимостта (20), въвеждаме нови обозначения:

x 2 \u003d (l cf + ∆ 1), (22)

y 2 \u003d (T avg + ∆ 2) 2, (23)

Преди да пристъпим към изчисленията, използвайки формули (22) и (23), ние формираме формата на нова таблица 6 с помощта на програматаExcel , съгласно предварително посочения алгоритъм, тогава получаваме

Таблица 6.

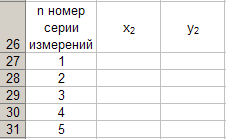
При изчисляване на x 2 и y 2 съгласно (22) и (23) е необходимо да се използват данните от таблици 4 и 5. Първо, ние изчислявамеx 2 и получените числа се въвеждат в таблица 6.

За да направите това, активирайте клеткатаБ. 27 и въведете формулата "\u003d B11 + B20" в нея от клавиатурата.

След това изчислете y 2 за това активираме клетката° С 27 и въведете формулата "\u003d (C11 + C20) ^ 2" в нея от клавиатурата.

В 27: С 27 и се довършва автоматично до клеткатаС 31.

Тогава таблица 6 ще бъде попълнена със следните данни

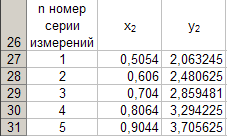
Според таблица 6 изграждаме графика на зависимосттаy 2 \u003d y 2 (x 2) (виж фиг. 5) съгласно описаната по-рано технология

Фигура 5 показва, че зависимосттаy 2 \u003d y 2 (x 2) се определя от уравнението

y 2 \u003d 4,08 86 x 2 - 0,002 3 (24)

Пристъпваме към изчисляване на функционалната зависимост (21). За това въвеждаме две спомагателни формули

x 3 \u003d l cf - ∆ 1, (25)

y 3 \u003d (T av - ∆ 2) 2. (26)

Изчислението по тези формули се извършва съгласно данните от таблици 4 и 5, а резултатите от тези изчисления се въвеждат в таблица 7. Първо, ние изчислявамеx 3 ... За да направите това, активирайте клеткатаБ. 34 и въведете формулата "\u003d B11-B20" в нея от клавиатурата.

След това изчислете y 3 за това активираме клетката° С 34 и въведете формулата "\u003d (C11-C20) ^ 2" в нея от клавиатурата.

Сега нека активираме диапазона от клеткиB 34: C 34 и автоматично попълване към клеткатаС 38.

Данните в тази таблица са както следва

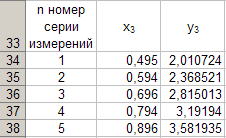
Функционална зависимосту 3 = у3 (х3 ) , построен съгласно таблица 7 е показан на фигура 6.

Фигура 6 предполага това

у3 = 4,00 7 3 х3 + 0,00 71 (27)

Стойности на наклонак според данните от уравнения (17), (24), (27) влизаме в таблица 8.

Програмираме формулата (12) и изчислявамежсъответстващи на всяка стойностк... Въвеждаме получените стойностиж в таблица 8. За да направите това, активирайте клетката° С41 и въведете формулата "\u003d (4 * PI () ^ 2) / B41" от клавиатурата. След това ще се довършим автоматично до клетката° С43.

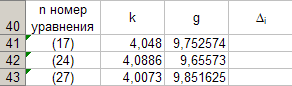
Сега изчисляваме средната стойностж според формулата

За да направите това, активирайте клетката° С45 и въведете формулата "\u003d (1/3) * SUM (C41: C43)" от клавиатурата.

Оказва се, че е равно на 9.75331, което приемаме за точна стойност. Грешката при определяне на тази стойностж изчислено по формулата

Δ 3 = макс | жi – жср| = макс | Δ i| (28)

За да направите това, активирайте клеткатад41 и въведете формулата "\u003d ABS (C41-C $ 45)" в нея от клавиатурата. След това ще се довършим автоматично до клеткатаD43.

Ние изчислявамеΔ i и го поставете в таблица 8. За да направите това, активирайте клеткатад45 и въведете формулата "\u003d MAX (D41: D43)" от клавиатурата.

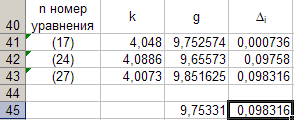
От данните в таблица 8 следва, чеΔ 3 \u003d 0,098316. Така че ускорениетож свободното падане, получено с това устройство, в резултат на непреки измервания, се оказа

g \u003d 9,7533 ± 0,0983.

Контролни въпроси

1. Какви са елементите на устройството за изучаване на трептенията на математическо махало.
2. Въз основа на какъв закон на механика се съставя уравнението за движение на махалото
3. При какви ограничения се получава уравнение, което симулира движението на математическо махало.
4. Какви вибрации се наричат \u200b\u200bхармонични.
5. Дайте дефиниция на амплитудата, фазата и честотата на трептенията.