Def . нехай,
,

.

Безліч називається замкнутим проміжком або замкнутим брусом в .

Безліч називається відкритим проміжком

або відкритим брусом в .

Def . мірою проміжків і називається величина:

(Точніше
).

Def . якщо
таке, що
то проміжок називається виродженим і
.

Властивості заходи проміжку:

а). позитивність:
, причому
тоді і тільки тоді, коли - виродилися.

б). Позитивна однорідність:.

в). адитивність:

* для
таких, що
;

* для
і

.

г). Монотонність заходи:.

Def . Діаметром бруса (проміжку) називається величина:

Відмітимо, що
і
- Це не одне і те ж. Наприклад, якщо - виродилися, то
, a
(взагалі кажучи).

При цьому: * ;

* ;*
.

Def . сукупність
подпромежутков проміжку називається розбиттям проміжку , Якщо: *;

*
; *
; *
; *
.

величина
називається параметром розбиття P(при цьому
).

Def . розбиття називається подрібненням розбиття , Якщо всі елементи розбиття отримані розбиттям елементів розбиття .

позначається:
. читається: дрібніше або крупніше .

Для відносини "крупніше - дрібніше" справедливо:

*. транзитивність -; *.
;

*.


; *.

|
.

§. Визначення кратного інтеграла

нехай
- брус (проміжок) в ,
- розбиття проміжку I. На кожному з проміжків розбиття відзначимо точку
.

отримаємо
розбиття із зазначеними точками для
.

величина
називається інтегральною сумою Рімана для функції f (x) На проміжку I по розподіленню з зазначеними точками
.

Def :
=
=
.

позначаючи - безліч функцій інтегрованих на брусі I запишемо:

Def : ε > 0 δ>0<.

Якщо для функції f(x) на Iі розбиття
- позначити через
- найбільше та найменше значення функції f(x) на I kто величини
=
і
=
називаються нижньої і верхньої сумами Дарбу.

§. Критерій Дарбу існування кратного інтеграла.

Т 0 . щоб функція
була інтегрована на брусі (Тобто
) Необхідно і достатньо, щоб

. Δ▲.

Визначено інтегрування функції по брусу в евклідовому просторі. А як функцію проінтегрувати за довільним обмеженому безлічі з евклідового простору?

Визначимо інтеграл від функції f по безлічі
.

Def : нехай
і
- обмежена, тобто
. функцію
назвемо характеристичної функцією безлічі M.

тоді:
≡
.

Визначення інтеграла по безлічі не залежить від того, який брус, що містить Мобраний, тобто

.

Це означає, що визначення інтеграла по безлічі коректно.

Необхідна умова інтегрованості.щоб функція f(x) на Мбула інтегрованою необхідно, щоб f(x) Була обмеженою на М. Δ▲.

§. Властивості кратних інтегралів.

1  . Лінійність: Безліч R Mфункцій інтегрованих на безлічі М -лінійне

простір, а
- лінійний функціонал.

2  . Умова нормування:
. Інша форма запису
по суті справи визначає міру довільного безлічі з евклідового простору.

3  . Якщо інтеграл по безлічі Лебеговой заходи нуль існує, то він

дорівнює нулю.

Примітка:безліч Мназивається безліччю Лебеговой заходи нуль,

якщо

такі, що
і
.

4  . а.;б.;

в.якщо
і - відокремлена від нуля на М, то

5  .
і f=gп.в. (Майже скрізь) на М, то
.

6  . Адитивність: Якщо
і
то

,

У загальному випадку:
.

Δ. Слід з рівності: ▲

7  . монотонність:
і
то
.

8  . Інтегрування нерівностей: якщо
і то

.

9  . нехай


. Для того щоб
, Необхідно і достатньо щоб існувала внутрішня точка М, в якій f (x)> 0 і неперервна.

10  . Интегрируемость модуля інтегрованої функції:
.

11  . Теорема про повну загальну середню:
,
на Мзберігає знак і
, то

.

якщо безліч М- докладно і f(x) - неперервна на
то
таке, що
.

12  . Для того щоб інтеграл від неотрицательной функції дорівнював 0

необхідно і достатньо, щоб f(x) = 0 майже скрізь на М.

13  . Теорема Фубіні.Для подвійного інтеграла:

нехай область
- прямокутник :. Тоді, за умови існування внутрішніх одноразових інтегралів, для знаходження подвійного інтеграла можна перейти до повторного інтегрування (див. Рис. А):

, або

Е

кщо область інтегрування НЕ прямокутник, теорема Фубіні все одно справедлива і має вигляд (див. рис. б):
. (*)

Примітка:Зовнішні межі інтегрування повинні бути константами, внутрішні межі інтегрування можуть залежати від змінної, по якій інтегрування ще належить.

Формула (*) може бути отримана з використанням характеристичної функції безлічі D.

Для багаторазового інтеграла:

Нехай ідеякі підмножини евклідових просторів і . Визначимо декартовій твір цих множин, що є підмножиною евклідового простору
:.

Тоді теорема Фубіні для
має вигляд:
.

Теорема справедлива і для брусів Xі Y, І для більш складних конфігурацій.

приклади:

1 0 . обчислити
, Якщо межа області
задана рівняннями:

. Знаходячи точки перетину кривих визначають кордон області, отримуємо дві точки:
і
. Тоді можлива розстановка меж інтегрування при переході до повторних інтегралів дає:

а).
;

2

0 . Змінити порядок інтегрування в повторному інтегралі:
.

–

.

рецепт:При розстановці меж інтегрування в подвійному інтегралі рекомендується починати з зовнішніх меж інтегрування.

3

0 . обчислити:
, якщо

Перехід до повторних інтегралів дає:
.

При цьому, в потрійному інтегралі розстановку меж треба починати з внутрішніх меж інтегрування. Потім спроектувати область Vна площину xOy

розставивши межі в області D- лежить в площині xOy.

4 0 . Змінити порядок інтегрування в повторному інтегралі:
.

Зупинимося дещо докладніше на роботах Остроградського по кратним интегралам.

Формула Остроградського для перетворення потрійного інтеграла в подвійний, яку ми пишемо зазвичай у вигляді

де div A - дивергенція поля вектора А,

Аn - скалярний добуток вектора А на одиничний вектор зовнішньої нормалі n граничної поверхні, в математичній літературі нерідко пов'язувалася раніше з іменами Гаусса і Гріна.

Насправді в роботі Гаусса про тяжінні сфероидов можна угледіти тільки вельми окремі випадки формули (1), наприклад при P = x, Q = R = 0 і т. П. Що стосується Дж. Гріна, то в його праці з теорії електрики і магнетизму формули (1) зовсім немає; в ньому виведено інше співвідношення між потрійним і подвійним інтегралами, саме, формула Гріна для оператора Лапласа, яку можна записати у вигляді

Звичайно, можна вивести формулу (1) і з (2), вважаючи

і точно так же можна отримати формулу (2) з формули (1), але Грін цього і не думав робити.

де зліва стоїть інтеграл за обсягом, а праворуч інтеграл по граничної поверхні, причому суть направляючі косинуси зовнішньої нормалі.

Паризькі рукописи Остроградського свідчать, з повною переконливістю, що йому належить і відкриття, і перше повідомлення інтегральної теореми (1). Вперше вона була висловлена ​​і доведена, точно так, як це роблять тепер в "Доказ однієї теореми інтегрального числення", представленому Паризької Академії наук 13 лютого 1826, після чого ще раз була сформульована в тій частині "Мемуари про поширення тепла всередині твердих тіл", Яку Остроградський представив 6 серпня 1827 г." Мемуар "було дано на відгук Фур'є і Пуассону, причому останній його, безумовно читав, як свідчить запис на перших сторінках обох частин рукопису. Зрозуміло, Пуассону і не спадало на думку приписувати собі теорему, з якою він познайомився в творі Остроградського за два роки до представлення своєї роботи на теорії пружності.

Що стосується взаємини робіт по кратним интегралам Остроградського та Гріна, нагадаємо, що в "Замітці з теорії теплоти" виведена формула, обіймаються власну формулу Гріна, як вельми окремий випадок. Незвична тепер символіка Коші, вжита Остроградським в "Замітці", до недавнього часу приховувала від дослідників це важливе відкриття. Зрозуміло, за Гріном залишається честь відкриття і першої публікації в 1828 р носить його ім'я формули для операторів Лапласа.

Відкриття формули перетворення потрійного інтеграла в подвійний допомогло Остроградскому вирішити проблему варіювання п-кратного інтеграла, саме, вивести знадобиться там загальну формулу перетворення інтеграла від вирази типу дивергенції по п-мірної області та інтеграл по обмежує її сверхповерхності S з рівнянням L (x, y, z, ...) = 0. Якщо дотримуватися колишніх позначень, то формула має вигляд

Втім, Остроградський не застосовував геометричних образів і термінів, якими користуємося ми: геометрія багатовимірних просторів в той час ще не існувало.

В "Мемуарах про обчислення варіацій кратних інтегралів" розглянуті ще два важливих питання теорії таких інтегралів. По-перше, Остроградський виводить формулу заміни змінних в багатовимірному інтеграл; по-друге, вперше дає повний і точний опис прийому обчислення п- кратного інтеграла за допомогою п послідовних інтеграцій перспективами кожного із змінних у відповідних межах. Нарешті, з формул, що містяться в цьому мемуарах, легко виводиться загальне правилодиференціювання по параметру багатовимірного інтеграла, коли від цього параметра залежить не тільки подинтегральная функція, але і межа області інтегрування. Назване правило випливає з наявних в мемуарах формул настільки природним чином, що пізніші математики навіть ототожнювали його з одною з формул цього мемуара.

Заміні змінних в кратних інтеграли Остроградський присвятив спеціальну роботу. Для подвійного інтеграла відповідне правило вивів за допомогою формальних перетворень Ейлер, для потрійного - Лагранж. Однак, хоча результат Лагранжа вірний, міркування його були неточними: він як би виходив з того, що елементи обсягів в старих і нових змінних - координатах - між собою рівні. Аналогічну помилку допустив спочатку в тільки що згаданому виведення правила заміни змінних Остроградський. У статті "Про перетворення змінних в кратних інтеграли" Остроградський розкрив помилку Лагранжа, а також вперше виклав той наочний геометричний метод перетворення змінних в подвійному інтегралі, який, в кілька більш суворому оформленні, викладається і в наших посібниках. Саме, при заміні змінних в інтегралі за формулами, область інтегрування розбивається координатними лініями двох систем u = const, v = const на нескінченно малі криволінійні чотирикутники. Тоді інтеграл можна отримати, складаючи спочатку ті його елементи, які відповідають нескінченно вузької криволінійної смузі, а потім, продовжуючи підсумовувати елементи смугами, поки вони все не будуть вичерпані. Нескладний підрахунок дає для площі, яка з точністю до малих вищого порядку може розглядатися як паралелограм, вираз, де, вибирається так, щоб площа була позитивною. У підсумку виходить відома формула

Для функції двох змінних, заданої як z = f(x, y) .

Записується подвійний інтеграл так:

тут D- плоска фігура, обмежена лініями, вираження яких (рівності) дані в завданні обчислення подвійного інтеграла. Ліворуч і праворуч - равенствами, в яких зліва змінна x, А зверху і знизу - равенствами, в яких зліва змінна y. Це місце і далі - одне з найважливіших для розуміння техніки обчислення подвійного інтеграла.

Обчислити подвійний інтеграл - значить знайти число, що дорівнює площі згаданої фігури D .

Поки ми не торкаємося визначення подвійного інтеграла , А будемо вчитися його обчислювати. Зрозуміти, що таке подвійний інтеграл, простіше, коли вирішені кілька завдань на його обчислення, тому визначення подвійного інтеграла ви знайдете в кінці цього уроку. Трохи забігаючи вперед, можна лише відзначити, що визначення подвійного інтеграла також пов'язано зі згадуваною фігурою D .

У разі якщо фігура Dявляє собою прямокутник, все лінії, що обмежують її - це прямі лінії. якщо фігура D- криволинейна, то ліворуч і праворуч вона обмежена прямими, а зверху і знизу - кривими лініями, заданими равенствами, які дані в завданні. Бувають і випадки, коли фігура D- трикутник, але про такі випадки трохи далі.

Для обчислення подвійного інтеграла потрібно, таким чином, розсортувати лінії, огранивать фігуру D, Яка має суворе назва - область інтегрування. Розсортувати на ліві і праві і на верхні і нижні. Це потрібно при зведенні подвійного інтеграла до повторного інтеграла - методі обчислення подвійного інтеграла.

Випадок прямокутної області:

Випадок криволінійної області:

А це вже рішення знайомих нам певних інтегралів, в яких задані верхній і нижній межі інтегрування. Вирази, що задають лінії, які обмежують фігуру D, Будуть межами інтегрування для звичайних визначених інтегралів, до яких ми вже підходимо.

Зведення подвійного інтеграла до повторного

Випадок прямокутної області

Нехай для такої функції існує подвійний інтеграл

щоб обчислити цей подвійний інтеграл , Потрібно звести його до повторного інтеграла, який має вигляд

.

Спочатку потрібно обчислювати внутрішній (правий) певний інтеграл, потім - зовнішній (лівий) певний інтеграл.

Можна і поміняти ролями xі y

.

Приклад 1.Обчислити подвійний інтеграл

Обчислюємо внутрішній (правий) інтеграл, вважаючи ігрек константою. Отримуємо.

.

Приклад 2.Обчислити подвійний інтеграл

,

Рішення. Зводимо даний подвійний інтеграл до повторного інтеграла

На кресленні будуємо область інтегрування:

Тепер обчислюємо зовнішній (лівий) інтеграл від обчисленого тільки що внутрішнього (правого):

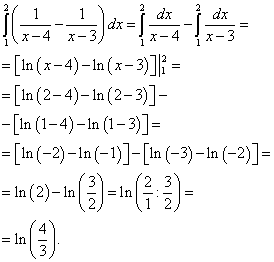
Результат і буде рішенням даного подвійного інтеграла.

Обчислити подвійний інтеграл самостійно, а потім подивитися рішення

Випадок криволінійної або трикутної області

Нехай знову дана функція двох змінних f(x, y) , А обмеження для D: Вже дещо іншого виду:

Цей запис означає, що фігуру Dзліва і справа обмежують, як і в випадку прямолінійної області - прямі x = aі x = b, Але знизу і зверху - криві, які задані рівняннями і. Іншими словами, і - функції.

Нехай для такої функції також існує подвійний інтеграл

Щоб обчислити цей подвійний інтеграл, потрібно звести його до повторного інтеграла, який має вигляд

.

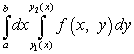Тут межі інтегрування aі b- числа, а й - функції. У разі трикутної області одна з функцій або - це рівняння прямої лінії. Такий випадок буде розібраний в прикладі 3.

Як і в випадку прямолінійної області, спочатку потрібно обчислювати правий певний інтеграл, потім - лівий певний інтеграл.

Точно так само можна поміняти ролями xі y. Тоді повторний інтеграл матиме вигляд

.

Такий повторний інтеграл потрібно вирішувати точно так же: спочатку - внутрішній (правий) інтеграл, потім - зовнішній (лівий).

Приклад 5.Обчислити подвійний інтеграл

,

Рішення. Зводимо даний подвійний інтеграл до повторного інтеграла

.

На кресленні будуємо область інтегрування і бачимо, що вона трикутна:

Обчислюємо внутрішній (правий) інтеграл, вважаючи ікс константою. Отримуємо.

Тепер обчислюємо зовнішній (лівий) інтеграл від обчисленого тільки що внутрішнього (правого). Спочатку представляємо цей інтеграл у вигляді суми інтегралів:

.

Обчислюємо перший доданок:

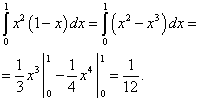
Обчислюємо другий доданок:

Обчислюємо третій доданок:

Отримуємо суму, яка і буде рішенням даного подвійного інтеграла:

.

Приклад 6.Обчислити подвійний інтеграл

Рішення. Зводимо даний подвійний інтеграл до повторного інтеграла

На кресленні будуємо область інтегрування:

Обчислюємо внутрішній (правий) інтеграл, вважаючи ікс константою. Отримуємо.

.

Тепер обчислюємо зовнішній (лівий) інтеграл від обчисленого тільки що внутрішнього (правого):

Результат і буде рішенням даного подвійного інтеграла.

x-правильним і неправильна, y-правильним і неправильна області інтегрування

Трапляється, область інтегрування подвійного інтеграла обмежена такими лініями, що виникає необхідність розбити область інтегрування на частини і вирішувати кожен відповідний повторний інтеграл окремо. Це випадки, коли:

1) область інтегрування є фігурою, що має у вигляді нижньої чи верхньої (лівої чи правої) межі дві або більше двох прямих або кривих ліній;

2) область інтегрування є фігурою, кордон якої прямі перетинають більш ніж в двох точках.

Якщо вищесказане відноситься до лівої чи правої кордоні області інтегрування, тобто обмеження, заданих лініями, вираженими через x, То область інтегрування називається x-неправильно. Якщо ж пряма y = y0 перетинає відповідну кордон лише в одній точці і якщо кордоном служить лише одна пряма або крива, то область інтегрування називається x-правильним

Аналогічно, якщо кордон, задану лініями, вираженими через y, пряма x = x0 перетинає більш ніж в одній точці або якщо кордоном служать більше одній прямій або кривій, то область інтегрування називається y-неправильно. Вивести тепер ознаки y-правильним області, мабуть, зовсім просто.

До сих пір ми розглядали приклади з x-неправильно і y-правильним областями інтегрування. Тепер розглянемо випадки, коли умова правильності порушується.

Приклад 7.Обчислити подвійний інтеграл, область інтегрування якої обмежена лініями y = x , xy = 1 , y = 2 .

Рішення. Область інтегрування є y-неправильно, так як її нижню межу можна задати однією лінією y = y(x) . Як видно на малюнку вище, нижня межа складається з y = x(Темно-бордова) і xy= 1 (зелена). Тому прямий x= 1 (чорна) можемо розбити область інтегрування на дві частини - і.

Обчислюється цей подвійний інтеграл так:

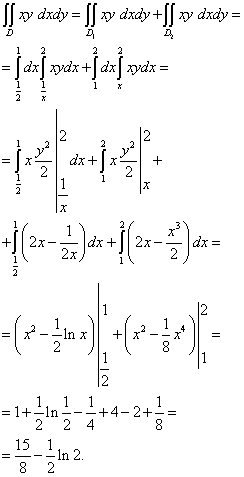
Зміна порядку інтегрування

Як вже зазначалося вище, після приведення подвійного інтеграла до повторного інтеграла, можна поміняти змінні xі yролями, або, інакше кажучи, поміняти порядок інтегрування.

Зміна порядку інтегрування образно може бути описана наступними словами О "Генрі:" Так поводиться мешканець джунглів - звір, потрапивши в клітину, і так поводиться мешканець клітини - людина, заблукавши в джунглях сумнівів ". Результат, так само по О" Генрі один і той же: "Чалмерс розірвав лист на тисячу дрібних клаптиків і почав мучити свій дорогий килим, ходячи по ньому взад і вперед". ( Про "Генрі. Шехерезада з Медісон-скверу.)

Тоді, якщо лівий інтеграл у нас по змінної x, А правий - по y, То після зміни порядку інтегрування все буде навпаки. Тоді межі інтегрування для "нового" Ігрека потрібно "запозичити" у "старого" ікси, а межі інтегрування для "нового" ікси отримати у вигляді зворотної функції, Дозволивши щодо ікси рівняння, задавати межа для Ігрека.

Приклад 8.

.

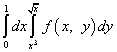Рішення. Після зміни порядку інтегрування інтеграл по Ігрек стане лівим, а інтеграл по Іксу - правим. Межі інтегрування для "нового" Ігрека запозичимо у "старого" ікси, тобто нижня межа дорівнює нулю, а верхній - одиниці. Межі інтегрування для "старого" Ігрека задані рівняннями і. Дозволивши ці рівняння щодо ікси, отримаємо нові межі інтегрування для ікси:

(Нижній) і (верхній).

Таким чином, після зміни порядку інтегрування повторний інтеграл запишеться так:

.

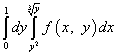Після зміни порядку інтегрування в подвійному інтегралі нерідко область інтегрування перетворюється в y-неправильно або x-неправильно (див. попередній параграф). Тоді потрібно розбити область інтегрування на частини і вирішувати кожен відповідний повторний інтеграл окремо.

Оскільки розбиття області інтегрування на частини представляє певні труднощі для багатьох студентів, щось не обмежимося прикладом, наведеним у попередньому параграфі, а розберемо ще пару прикладів.

Приклад 9.Змінити порядок інтегрування для повторного інтеграла

.

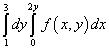Рішення. Отже, область інтегрування даного повторного інтеграла обмежена прямими y = 1 , y = 3 , x = 0 , x = 2y .

При інтегруванні в іншому порядку нижня межа області складається з двох прямих: ABі BC, Які задані рівняннями y= 1 і y = x/ 2, що видно на малюнку нижче.

Вихід з такої невизначеності полягає в розбитті області інтегрування на дві частини. Ділити область інтегрування буде пряма BМ. Нові межі інтегрування обчислюємо, знаходячи зворотну функцію. Відповідно до цього рішення повторний інтеграл після зміни порядку інтегрування буде рівним сумі двох інтегралів:

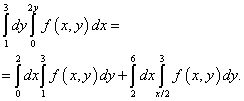
Природно, таким же буде рішення подвійного інтеграла, який зводиться до повторного інтеграла, яке у умови цього прикладу.

Приклад 10.Змінити порядок інтегрування для повторного інтеграла

.

Рішення. Отже, область інтегрування повторного інтеграла обмежена прямими x = 0 , x= 2 і кривими і.

Як видно на малюнку нижче, пряма, паралельна осі 0x, Буде перетинати нижню межу області інтегрування більш ніж в двох точках.

Тому розіб'ємо область інтегрування на три частини прямими, які на малюнку накреслені чорним. Нові межі інтегрування обчислюємо, знаходячи зворотну функцію. Межі для трьох нових областей інтегрування будуть наступними.

Відповідно до цього рішення повторний інтеграл після зміни порядку інтегрування буде рівним сумі трьох інтегралів:

Тій же сумі трьох інтегралів буде дорівнює і подвійний інтеграл, який зводиться до повторного інтеграла, яке у умови цього прикладу.

І все ж обставини непереборної сили нерідко заважають студентам вже на попередньому етапі - розстановці меж інтегрування. Тривога і сум'яття не позбавлені деякого підстави: якщо для розбиття області інтегрування на частини зазвичай досить придивитися до креслення, а для вирішення повторного інтеграла - таблиці інтегралів, то в розстановці меж інтегрування потрібен деякий досвід тренувань. Пробіжимо приклад, в якому зупинимося тільки на розстановці меж інтегрування і - майже на автоматі - на розбитті області і опустимо саме рішення.

Приклад 11.Знайти межі інтегрування подвійного інтеграла, якщо область інтегрування Dзадана в такий спосіб:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Рішення. В явному вигляді (через xі y"Без домішок") лінії, що обмежують область інтегрування, не задані. Так як для ікси ними найчастіше виявляються прямі, що стосуються в одній точці верхньої і нижньої меж, виражених через ігрек, то підемо саме цим шляхом. Тим більше, що при зміні порядку інтегірованія ми отримаємо область інтегрування з такою ж площею. Дозволимо нерівності щодо ігреки отримаємо:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

Будуємо отримані лінії на креслення. Межами інтегрування по Іксу дійсно служать лінії x= 0 і x= 2. Але область інтегрування виявилася y-неправильно, так як її верхню межу можна задати однією лінією y = y(x) .

Завантажити з Depositfiles

лекції 5-6

Тема2. Кратні інтеграли.

Подвійний інтеграл.

Контрольні питання.

1. Подвійний інтеграл, його геометричний і фізичний зміст

2. Властивості подвійного інтеграла.

3. Обчислення подвійного інтеграла в декартових координатах.

4. Заміна змінних в подвійному інтегралі. Обчислення подвійного інтеграла в полярних координатах.

нехай функція z = f (x , y) Визначена в обмеженій замкненій області Dплощині. розіб'ємо область Dдовільним чином на nелементарних замкнутих областей  1 , … , n, Що мають площі   1 , …,   nі діаметри d 1 , …, d n відповідно. позначимо dнайбільший з діаметрів областей  1 , … ,  n. У кожній області  kвиберемо довільну точку P k (x k , y k) І складемо інтегральну сумуфункції f(x, y)

S =
(1)

Визначення. подвійним інтеграломфункції f(x, y) По області Dназивається межа інтегральної суми

, (2)

якщо він існує.

Зауваження. інтегральна сума Sзалежить від способу розбиття області Dі вибору точок P k (k=1, …, n). Однак, межа
, Якщо він існує, не залежить від способу розбиття області Dі вибору точок P k .

Достатня умова існування подвійного інтеграла. Подвійний інтеграл (1) існує, якщо функція f(x, y) неперервна в Dза винятком кінцевого числа кусочно-гладких кривих і обмежена в D. Надалі будемо вважати, що всі розглянуті подвійні інтеграли існують.

Геометричний сенс подвійного інтеграла.

якщо f(x, y) ≥0 в області D, То подвійний інтеграл (1) дорівнює обсягу «циліндричного" тіла, зображеного на малюнку:

V =
(3)

Циліндричне тіло обмежена знизу областю D, Зверху  частиною поверхні z = f (x , y), З боків  вертикальними відрізками прямих, що з'єднують кордону цієї поверхні і області D.

Фізичний сенс подвійного інтеграла. Маса плоскої пластини.

Нехай задана плоска пластина Dз відомою функцією щільності γ ( х,у), Тоді розбиваючи пластину D на частини D iі вибираючи довільні точки
, Отримаємо для маси пластини
, Або, порівнюючи з формулою (2):

(4)

4. Деякі властивості подвійного інтеграла.

Лінійність.якщо З- числова константа, то

Адитивність.якщо область D «Розбита" на області D 1 і D 2, то

3) Площа обмеженою області Dдорівнює

(5)

Обчислення подвійного інтеграла в декартових координатах.

Нехай задана область

Малюнок 1

D = { (x , y ): a ≤ x ≤ b , φ 1 (x ) ≤ y≤ φ 2 (x ) } (6)

область D укладена в смузі між прямими x = a , y = b, Знизу і зверху обмежена відповідно кривими y = φ 1 (x ) і y = φ 2 (x ) .

Подвійний інтеграл (1) по області D(4) обчислюється переходом до повторного інтеграла:

(7)

Цей повторний інтеграл обчислюється таким чином. Спочатку обчислюється внутреннійінтеграл

по змінній y, при цьому xсчітаетсяпостоянной. В результаті вийде функція від змінної x, А потім обчислюється «зовнішній» інтеграл від цієї функції по змінній x .

Зауваження. Процес переходу до повторного інтеграла за формулою (7) часто називають розстановкою меж інтегрування в подвійному інтегралі. При розстановці меж інтегрування потрібно пам'ятати два моменти. По-перше, нижня межа інтегрування не повинен перевищувати верхньої, по-друге, межі зовнішнього інтеграла повинні бути константами, а внутрішнього повинні в загальному випадку залежати від змінної інтегрування зовнішнього інтеграла.

Нехай тепер область Dмає вигляд

D = { (x , y ) : c ≤ y ≤ d , ψ 1 (y ) ≤ x ≤ ψ 2 (y ) } . (8)

тоді

. (9)

Припустимо, що область Dможна представити у вигляді (6) і (8) одночасно. Тоді має місце рівність

(10)

Перехід од одного повторного інтеграла до іншого в рівність (10) називається зміною порядку інтегруванняв подвійному інтегралі.

Приклади.

1) Змінити порядок інтегрування в інтегралі

Рішення. По виду повторного інтеграла знаходимо область

D = { (x , y ): 0 ≤ x ≤ 1, 2 x ≤ y≤ 2 } .

зобразимо область D. За малюнком бачимо, що ця область розташована в горизонтальній смузі між прямими y =0, y= 2 і між лініями x =0 і x= D

Іноді для спрощення обчислень роблять заміну змінних:

,
(11)

Якщо функції (11) безперервно діфференцируєми і визначник (Якобіан) відмінний від нуля в даній області:

(12)

Міністерство освіти і науки Російської Федерації

Курсова робота

З дисципліни: Вища математика

(Основи лінійного програмування)

На тему: кратний інтеграли

Виконав: ______________

Викладач: ___________

Дата ___________________

оцінка _________________

підпис ________________

ВОРОНІЖ 2008

1 Кратні інтеграли

1.1 Подвійний інтеграл

1.2 Потрійний інтеграл

1.3 Кратні інтеграли в криволінійних координатах

1.4 Геометричні і фізичні додатки кратних інтегралів

2 Криволінійні і поверхневі інтеграли

2.1 Криволінійні інтеграли

2.2 Поверхневі інтеграли

2.3 Геометричні і фізичні додатки

Список використаної літератури

1 Кратні інтеграли

1.1 подвійний інтеграл

Розглянемо в площині Оху замкнуту область D, обмежену лінією L. Розіб'ємо цю область якими-небудь лініями на п частин

, А відповідні найбільші відстані між точками в кожній з цих частин позначимо d 1, d 2, ..., d n. Виберемо в кожній частині точку Р i.

Нехай в області D задана функція z = f (x, y). Позначимо через f (P 1), f (P 2), ..., f (P n) значення цієї функції в обраних точках і складемо суму творів виду f (P i) ΔS i:

, (1)

звану інтегральною сумою для функції f (x, y) в області D.

Якщо існує один і той же межа інтегральних сум (1) при

і, що не залежить ні від способу розбиття області D на частини, ні від вибору точок P i в них, то він називається подвійним інтегралом від функції f (x, y) по області D і позначається . (2)

Обчислення подвійного інтеграла по області D, обмеженої лініями

x = a, x = b (a< b), где φ 1 (х) и φ 2 (х) непрерывны на (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла: = (3)

1.2 потрійний інтеграл

Поняття потрійного інтеграла вводиться за аналогією з подвійним інтегралом.

Нехай в просторі задана деяка область V, обмежена замкнутою поверхнею S. Задамо в цій замкнутій області безперервну функцію f (x, y, z). Потім розіб'ємо область V на довільні частини Δv i, вважаючи обсяг кожної частини рівним Δv i, і складемо інтегральну суму виду

, (4)

межа при

інтегральних сум (11), що не залежить від способу розбиття області V і вибору точок P i в кожної підобласті цій галузі, називається потрійним інтегралом від функції f (x, y, z) по області V: . (5)

Потрійний інтеграл від функції f (x, y, z) по області V дорівнює триразовому інтегралу по тій же області:

. (6)

1.3 Кратні інтеграли в криволінійних координатах

Введемо на площині криволінійні координати, звані полярними. Виберемо точку О (полюс) і виходить з неї промінь (полярну вісь).

Мал. 2 Рис. 3

Координатами точки М (рис. 2) будуть довжина відрізка МО - полярний радіус ρ і кут φ між МО і полярною віссю: М (ρ, φ). Відзначимо, що для всіх точок площини, крім полюса, ρ> 0, а полярний кут φ будемо вважати позитивним при вимірюванні його в напрямку проти годинникової стрілки і негативним - при вимірюванні в протилежному напрямку.

Зв'язок між полярними і декартовими координатами точки М можна задати, якщо поєднати початок декартової системи координат з полюсом, а позитивну піввісь Ох - з полярною віссю (рис. 3). Тоді x = ρcosφ, у = ρsinφ. Звідси

, Tg.

Задамо в області D, обмеженої кривими ρ = Φ 1 (φ) і ρ = Φ 2 (φ), де φ 1< φ < φ 2 , непрерывную функцию z = f(φ, ρ) (рис. 4).

(7)

У тривимірному просторі вводяться циліндричні і сферичні координати.

Циліндричні координати точки Р (ρ, φ, z) - це полярні координати ρ, φ проекції цієї точки на площину Оху і аппликата даної точки z (рис.5).

рис.5 Рис.6

Формули переходу від циліндричних координат до декартових можна задати наступним чином:

x = ρcosφ, y = ρsinφ, z = z. (8)

У сферичних координатах положення точки в просторі визначається лінійної координатою r - відстанню від точки до початку декартової системи координат (або полюса сферичної системи), φ - полярним кутом між позитивною полуосью Ох і проекцією точки на площину Оху, і θ - кутом між позитивною полуосью осі Оz і відрізком OP (рис.6). При цьому

Задамо формули переходу від сферичних координат до декартових:

x = rsinθcosφ, y = rsinθsinφ, z = rcosθ. (9)

Тоді формули переходу до циліндричних або сферичних координат в потрійному інтегралі будуть виглядати так:

, (10)

де F 1 і F 2 - функції, отримані при підстановці у функцію fвместо x, y, z їх виразів через циліндричні (8) або сферичні (9) координати.

1.4 Геометричні і фізичні додатки кратних інтегралів

1) Площа плоскої області S:

(11)

Приклад 1.

Знайти площу фігури D, обмеженої лініями

Цю площу зручно обчислювати, вважаючи у зовнішньої змінної. Тоді кордону області задаються рівняннями

і
обчислюється за допомогою інтегрування частинами: