Studio delle vibrazioni di un pendolo di filo e misurazione. Lavoro di laboratorio in fisica "studio delle leggi di un pendolo matematico"

Lavoro di laboratorio

Studio delle leggi di un pendolo matematico

Scopo del lavoro: Studia le leggi di un pendolo matematico e determina l'accelerazione di gravità

Attrezzatura: Pendolo (palla sospesa), righello, cronometro o orologio con lancetta dei secondi.

Breve teoria:

Un pendolo matematico è un oscillatore che è sistema meccanico costituito da un punto materiale situato su un filo inestensibile senza peso o su un'asta senza peso in un campo uniforme di forze gravitazionali.

La lunghezza del pendolo l è la distanza dal punto di sospensione al centro di gravità della palla.

Per un calcolo pratico del periodo di oscillazione, utilizzare la formula:

,

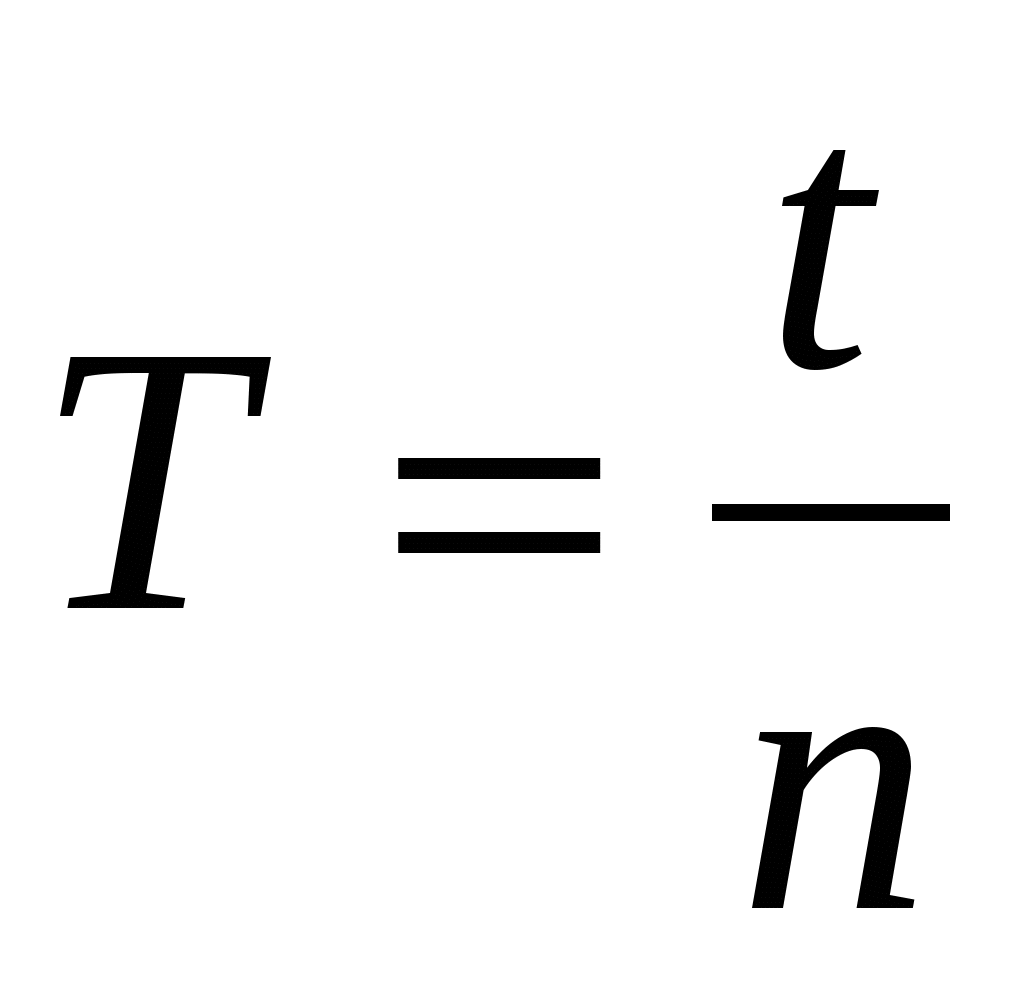dove T è il periodo di oscillazione,

t è il tempo di oscillazione,

n è il numero di vibrazioni complete.

Secondo le leggi dell'oscillazione, il periodo del pendolo può essere determinato dalla formula:

,

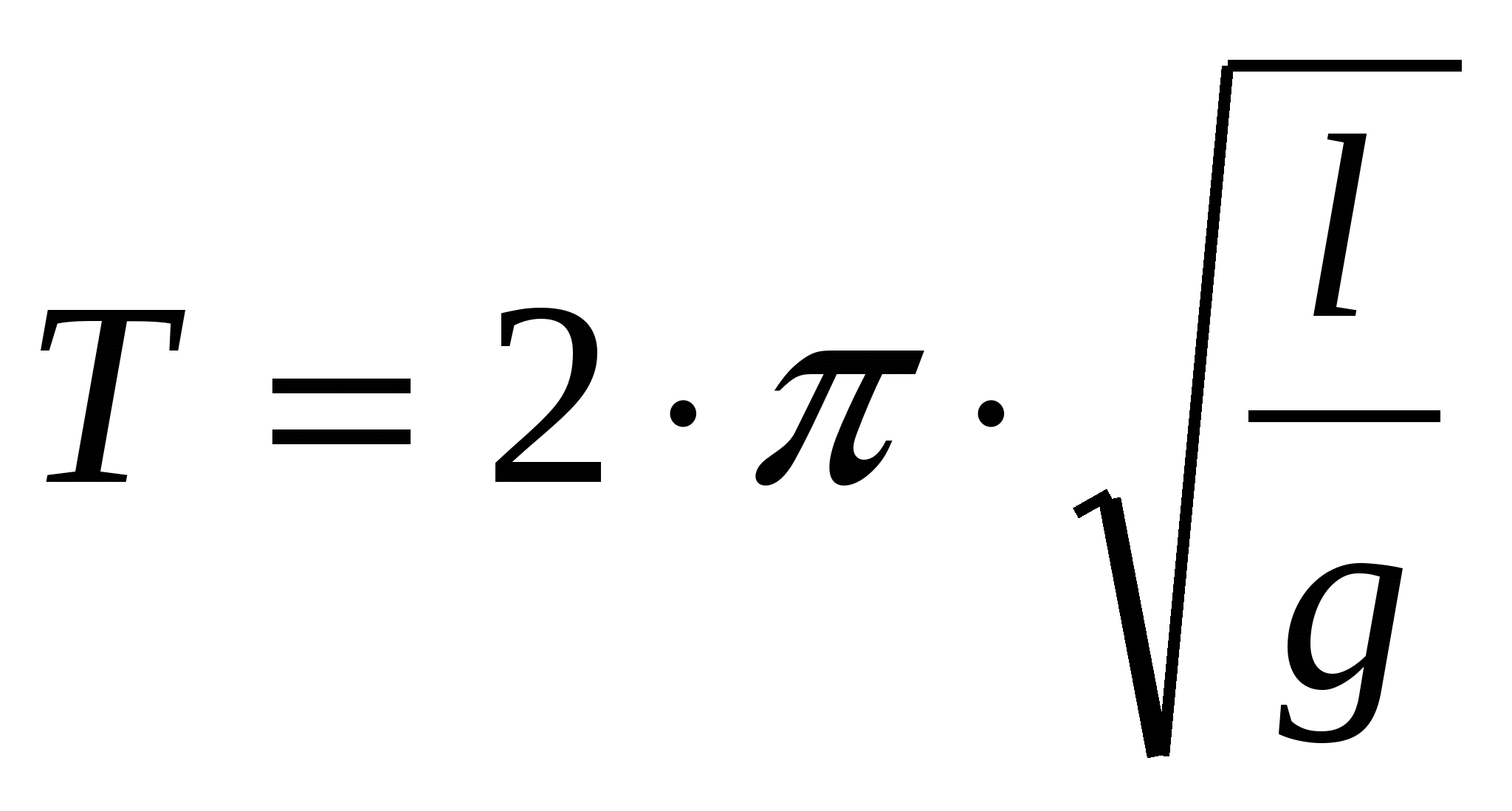Il periodo di oscillazione di un pendolo matematico non dipende dalla massa della palla.

NS Il periodo di oscillazione di un pendolo matematico è direttamente proporzionale alla lunghezza del pendolo e inversamente proporzionale all'accelerazione di gravità. Questa equazione è chiamata formula di Huygens.

Riferimento storico

Christian Huygens van Zuilichem (14 aprile 1629 - 8 luglio 1695). Fisico, matematico, meccanico, astronomo e inventore olandese. Nato a L'Aia. Ha studiato legge all'Università di Leiden, ma non ha smesso di studiare matematica. Basandosi sulle ricerche di Galileo, risolse una serie di problemi di meccanica. Nel 1656, all'età di 27 anni, progettò il primo orologio a pendolo con scappamento. La creazione di un orologio che misurasse il tempo con una precisione senza precedenti per quel tempo ebbe conseguenze di vasta portata per lo sviluppo dell'esperimento fisico e dell'attività pratica umana. Prima di allora, dopotutto, il tempo veniva misurato dal deflusso dell'acqua, dal fuoco di una torcia o di una candela. La teoria delle oscillazioni creata da Huygens nel 1673 fu una delle basi per comprendere in seguito la natura della luce.

Dalla formula di Huygens, mediante trasformazioni matematiche, si ottiene un'espressione per l'accelerazione di gravità:

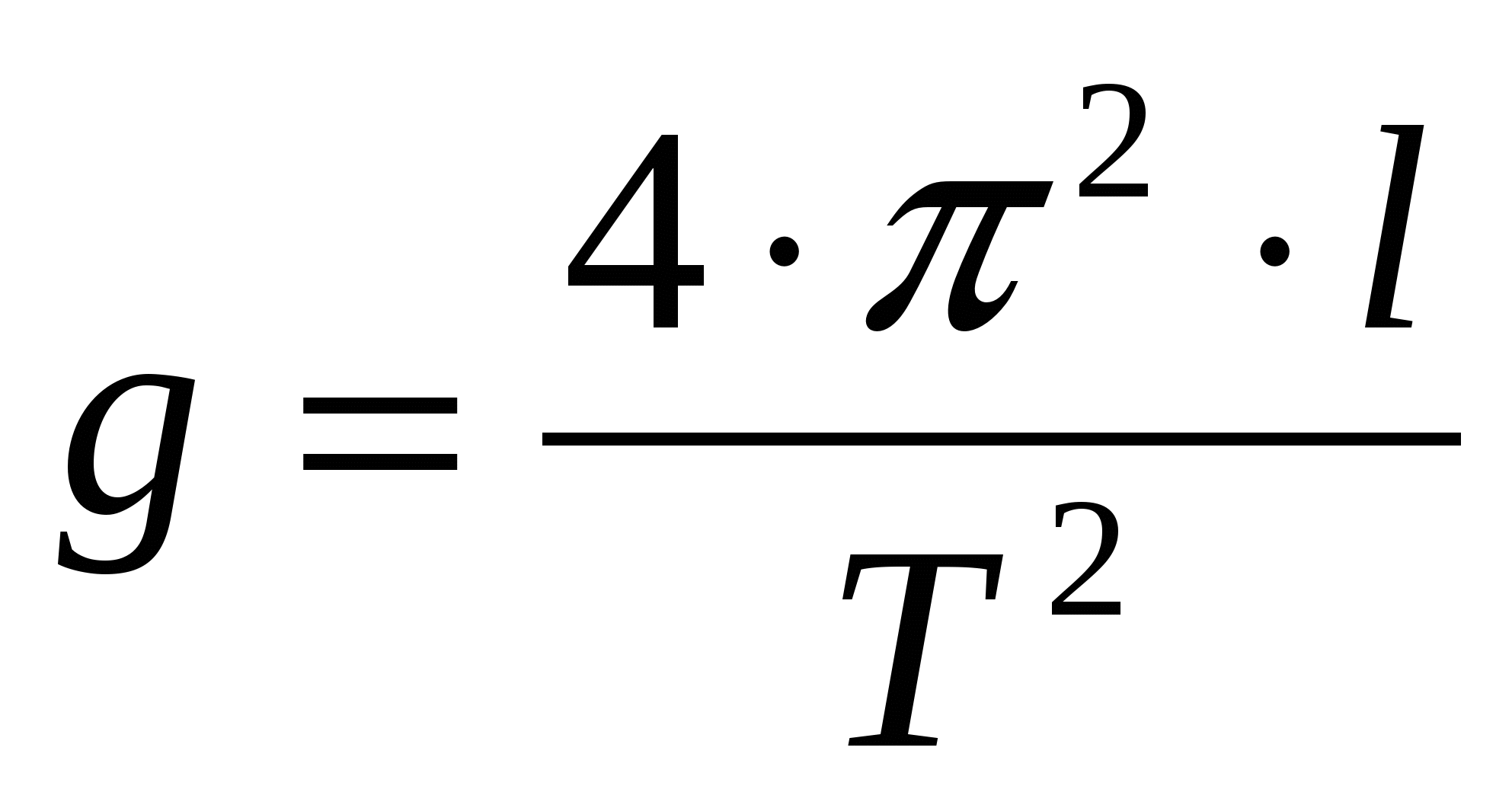
Un vero modello di pendolo matematico nei nostri esperimenti sarà una pallina sospesa su un sottile filo elastico. La dimensione della palla dovrebbe essere piccola rispetto alla lunghezza del filo. Questo permette di ipotizzare che tutta la massa sia concentrata in un punto, nel baricentro della palla.

Progresso:

Determinare il prezzo di divisione dei dispositivi:

righello …… ..m / div.

cronometro …… .s / div.

2. Determinare l'errore degli strumenti (l'errore assoluto degli strumenti è pari a ½ dell'intervallo di scala):

governate Δ io = …… ..m

cronometro Δ T= …… .s

Imposta la lunghezza massima del pendolo e misurala io 1 =… .m.

Avviare il pendolo (angolo di deflessione 10-15 0) e per il tempo T contare il numero di vibrazioni n(almeno 7).

Modificando il numero di vibrazioni, ripeti l'esperimento altre 3 volte.

t2 = ………, n2 = …………. T2 = ………,

t3 = ………, n3 = …………. T 3 = ………,

t4 = ………, n4 = …………. T4 = ………,

Modificare la lunghezza del pendolo io 2 =… .m e ripetere tutte le misurazioni.

Inserisci i dati nella tabella.

№ misure

Lunghezza del pendolo

io, m

№ Esperienza

Tempo di oscillazione,

t, s

Il numero di vibrazioni

n

periodo di oscillazione,

T, s

Valore medio del periodo, T av, s

Accelerazione di caduta libera, g, m/s 2.

Significare

accelerazione in caduta libera, g media, m/s 2.

l cf =

T Mer =

relativo: assoluto:

,

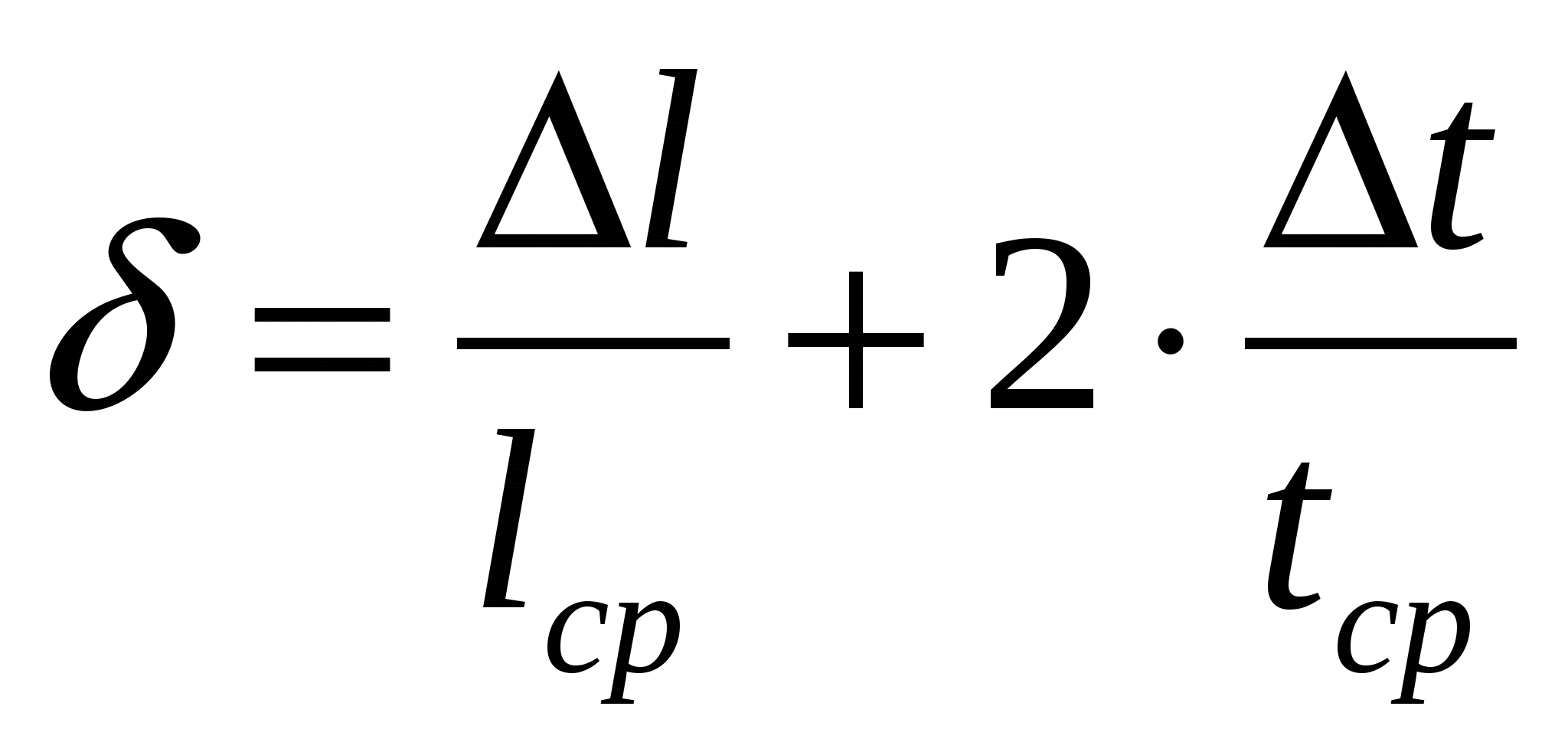
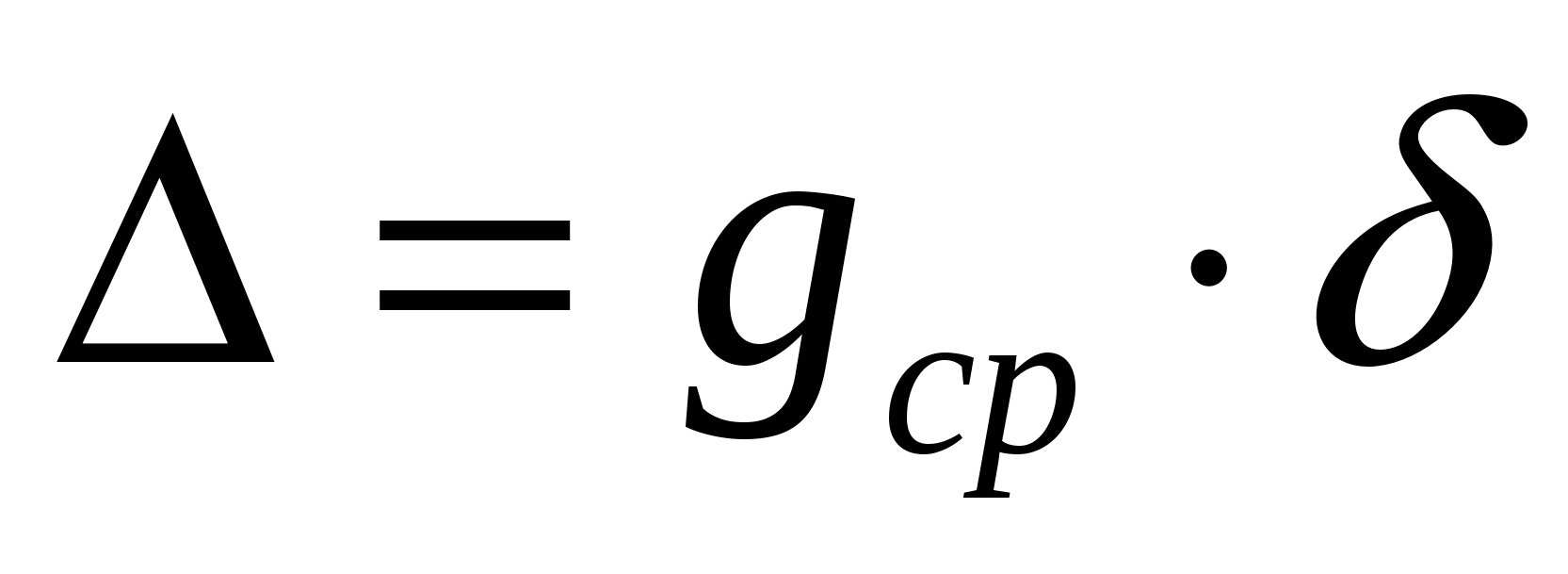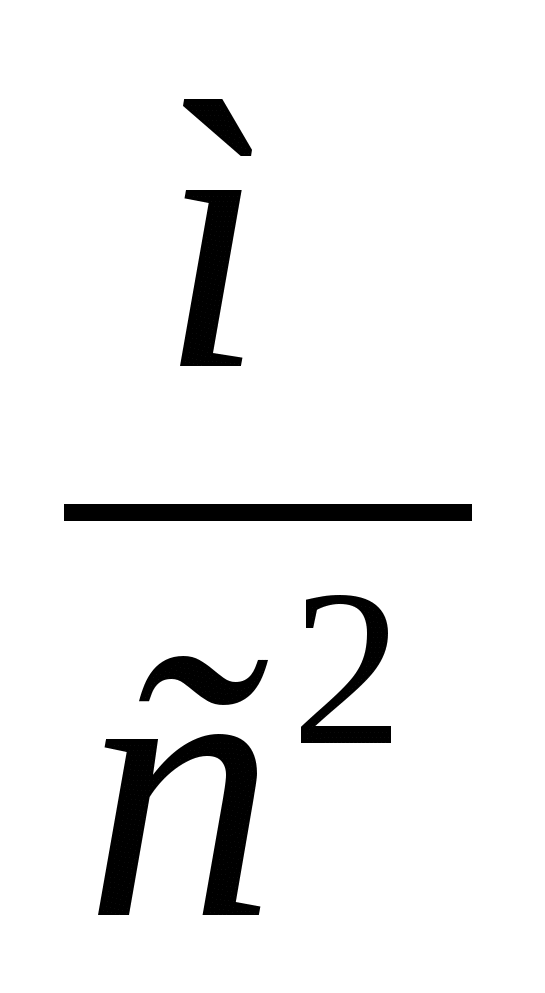
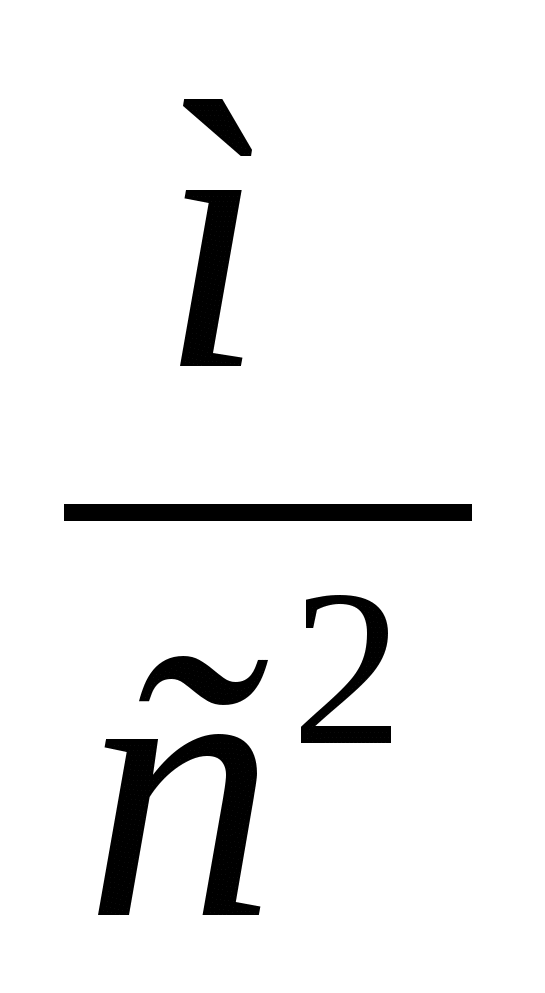
Domande di controllo:

Quanto dura un pendolo matematico con un periodo di 2 s?

Trova la massa del peso che, su una molla con una rigidità di 250 N/m, fa 20 vibrazioni in 16 s.

L'accelerazione di gravità sulla Luna è 1,7 m / s 2. Quale sarà il periodo di oscillazioni del pendolo matematico sulla Luna, se sulla Terra è uguale a 1 s? La risposta dipende dal peso del carico?

La coordinata del corpo oscillante cambia secondo la legge x = 0.5sin 45πt Qual è l'ampiezza e il periodo delle oscillazioni?

L'ampiezza delle oscillazioni continue del punto è 12 cm, la frequenza lineare è 14 Hz, la fase iniziale delle oscillazioni è 0. Scrivi l'equazione del moto del punto x = x (t).

Divisione scala

Differenza (nessun segno) tra i valori quantità fisica corrispondente alla divisione limite dei segni di scala. Nei dispositivi digitali, il gradino di discrezione funge da caratteristica che sostituisce il valore di divisione della scala.

a) selezionare sulla scala i due tratti digitalizzati più vicini;

c) la differenza di valori ( sottrarre il più piccolo dal più grande) per i tratti selezionati, dividere per il numero di divisioni.

h

Questa figura mostra una scala di un termometro su larga scala. Lo useremo per illustrare la regola per il calcolo del prezzo di divisione.

a) selezionare i tratti digitalizzati 20° С e 40° С

b) 10 divisioni (spazi) tra di loro

c) calcolare: (40° С - 20° С): 10 divisioni = 2° С/div.

Risposta: il prezzo delle divisioni = 2° С / div,

I dispositivi digitali non hanno una scala in modo esplicito e, al posto del prezzo di divisione, su di essi è indicato il prezzo dell'unità della cifra meno significativa del numero nella lettura del dispositivo.

NS


Esempio:

1) il prezzo di divisione della scala di questo dispositivo è 1 (unità convenzionali) / div.

2
) il prezzo di divisione della scala di questo dispositivo è 0,01 (unità convenzionali) / div.

3
) la divisione in scala di questo dispositivo è 0.1 (unità convenzionali) / div.

4) il prezzo di divisione della scala di questo dispositivo è 0.001 (unità convenzionali) / div.

IO. scopo del lavoro

Osservazioni dei movimenti oscillatori di un pendolo matematico, implementato su un dispositivo, il cui diagramma funzionale è mostrato in Figura 1.

Misura del periodo di oscillazione del pendolo a diverse lunghezze e ampiezze.

Determinazione del modo di isocronismo delle oscillazioni di un pendolo matematico.

Calcolo dell'accelerazione gravitazionale della palla dai risultati delle misurazioni specificate.

II ... Parte teorica

Si consideri un dispositivo costituito da una pallina fissata ad un punto fisso di sospensione mediante un filo inestensibile senza peso di una certa lunghezza (Fig. 1).

Se la dimensione della palla è molto inferiore alla lunghezza io fili, quindi la palla può essere considerata come un punto materiale; e se la massa della palla è molto maggiore della massa del filo, allora quest'ultimo può essere considerato senza peso. Un filo può anche essere considerato inestensibile, purché la gravità della sfera provochi un allungamento infinitesimale del filo.

Questo dispositivo permette di simulare il moto oscillatorio del cosiddetto pendolo matematico.

Riso. 1. Un dispositivo per studiare le oscillazioni di un pendolo matematico: 1. Una piastra metallica per stabilire l'angolo di deflessione del pendolo; 2. Piattaforma mobile; 3. Righello di misurazione.

Fig 2. Illustrazione dei movimenti oscillatori di un pendolo matematico.

Infatti, nello stato iniziale, il filo è diretto verticalmente verso il basso (posizione 1 in Figura 2). In questo caso, la forza F tensione e forza del filo mg i pesi della palla coincidono con la direzione del filo, ma diretti in senso opposto. Poiché il filo è inestensibile, entrambe le forze si equilibrano, ad es. F = mg ... La palla è ferma. Questo stato del pendolo è chiamato la sua posizione di equilibrio.

Portiamo il pendolo fuori dalla sua posizione di equilibrio deviando la palla dal suo stato iniziale di un angoloφ 0 (fig. 2). Quindi lascialo andare senza spingere. Per gravità mg la pallina comincerà a muoversi verso la posizione di equilibrio, dopo un po' la oltrepasserà, poi dall'altra parte della posizione di equilibrio si allontanerà da essa di un angolo inferiore aφ 0 e, sotto l'azione della gravità, si precipiterà nuovamente verso la posizione di equilibrio. In assenza di influenze esterne sulla palla, quest'ultima eseguirà il movimento descritto su un piano. Ovviamente la traiettoria della palla sarà un arco di cerchio di raggio io ... Questi movimenti sono chiamati vibrazioni.

A causa dell'azione della forza di resistenza sulla palla, le sue oscillazioni saranno smorzate, il che è evidenziato dal fatto che dopo ogni passaggio di equilibrio, ne devierà ad un angolo sempre più piccolo. Tuttavia, se questo processo viene osservato per un tempo abbastanza breve, il processo oscillatorio può essere riconosciuto come non smorzato.

Considera le forze che agiscono sulla palla in un momento arbitrario nel tempo T. Lascia che - l'angolo di deflessione del filo in questo momento. Scriviamo la seguente equazione della seconda legge di Newton per la direzioneτ coincidente con la tangente tracciata al punto della traiettoria della palla, in cui si trova nel momento considerato T.

ma τ = - mg sin φ (1)

Qui un - accelerazione tangenziale, m È la massa della palla. Il segno meno a destra in (1) tiene conto del fatto che quando ci si sposta dalla posizione di equilibrio verso l'alto, la forza di gravità impedisce questo movimento.

L'accelerazione angolare della palla è definita come la derivata seconda dell'angolo, cioè

. (2)

Tra accelerazione tangenziale un e angolare ε c'è una connessione ovvia

(3)

L'equazione (1) tenendo conto delle formule (2) e (3) assume la forma:

. (4)

Nell'equazione (4), la funzione sconosciuta(t) sta sotto il segno della derivata seconda. Tale equazione in matematica è chiamata equazione differenziale ordinaria del secondo ordine.

Può essere semplificato se teniamo conto che a piccoli angoliφ, misurato in radianti. Allora invece di (4) avremo

. (5)

L'equazione (5) descrive il movimento del pendolo. Viene anche chiamata equazione dell'oscillatore armonico.

Per sostituzione diretta, ci si può assicurare che la soluzione dell'Eq. (5) abbia la forma

, (6)

se indichiamo con

. (7)

Quindi, si può vedere che i cambiamenti nell'angoloφ nel tempo avviene secondo una legge sinusoidale. La quantitàφ 0 , uguale all'angolo massimo di deviazione dalla posizione di equilibrio è chiamata ampiezza delle vibrazioni armoniche. L'ampiezza dell'ampiezza in questo caso dipende dalla deviazione iniziale. Il valore sotto il segno del seno è chiamato fase. La fase cresce in proporzione al tempo. Il valore sotto il segno del seno è chiamato fase iniziale, che nel movimento considerato è uguale a zero.

La funzione seno, che determina la natura dei movimenti oscillatori, è una funzione periodica con periodo uguale a. Quest'ultimo significa che se dopo T designare il periodo di oscillazione del pendolo, quindi possiamo scrivere la seguente uguaglianza per la grandezza della fase

, (8)

dove è la frequenza angolare.

Ora, tenendo conto (7) per il periodo Avremo:

(9)

La relazione (9) indica che la linearizzazione dell'equazione (4) ha portato all'equazione (5), la cui soluzione ammette l'indipendenza T sull'ampiezza φ 0.

Tali fluttuazioni sono chiamate isocrone.

La formula (9) può anche essere rappresentata come segue:

kl, (10)

dove attraverso

(11)

denota la pendenza della dipendenza funzionale lineare della funzione T 2 dall'argomento l.

Di conseguenza, l'isocronismo delle oscillazioni del pendolo è verificato dalla validità della relazione (10) secondo i valori misurati del periodo T a valori diversi io relativo allo stesso angoloφ 0 .

La dipendenza funzionale costruita dai punti sperimentali permette di determinare la pendenza K, attraverso il valore numerico di cui l'accelerazione G la caduta libera della palla è calcolata come segue:

. (12)

Inoltre, per singole misurazioni T e l accelerazione g può essere calcolato anche da questo rapporto:

(13)

III ... Procedura dell'esperimento

Poiché la linearizzazione dell'equazione (4), che ha portato all'equazione (5), che descrive le oscillazioni isocrone, si basa sul presupposto, è ovvio che l'intervallo isocrono è determinato dai valori dell'angoloφ 0 in cui esiste una dipendenza lineare.

Quindi, per definire un intervallo di valoriφ 0 , per cui vale la relazione (10), è necessario per più valoriφ 0 effettuare misurazioni che consentono di tracciare le dipendenze, quindi dalle dipendenze funzionali specificate calcolare la pendenza K e per gli angoli selezionatiφ 0 calcolare i valori G secondo (12), e confrontarli con il valore generalmente accettato g = 9,8 m/s 2. Quegli angoli φ 0 per cui il valore calcolato G tenendo conto dell'errore di misurazione, salverà gli stessi valori numerici e determinerà l'intervallo di isocronismo delle oscillazioni realizzate da questo dispositivo.

L'ordine delle misurazioni è il seguente: viene selezionato un valore dell'angolo specificoφ 0 , per cui è necessario deviare la palla dalla posizione di equilibrio, viene impostata la lunghezza del pendolo, viene eseguito un esperimento, durante il quale viene misurato il periodo T ... L'esperimento viene eseguito più volte in modo che ad un angolo fissoφ 0 è necessario avere da tre a cinque valori misurati l e T.

Questa sarà la prima serie di misurazioni sul piano ( T 2, l ) darà solo un punto. Per controllare la formula (10) ad un dato angoloφ 0 è necessario produrre diversi di questi lotti.

Si propone di effettuare cinque di queste serie di misurazioni per ciascuno degli angoli.φ 0 , per cui vengono selezionati i seguenti tre angoli:φ 0 = 10 circa; φ 0 = 20 circa; 0 = 30 о.

Più valori misurati l e T per l'angolo selezionatoφ 0 le loro medie aritmetiche sono calcolate dalle formule:

, (14)

dove n - numero di misurazioni.

A seguito delle misurazioni, lo studente dovrà compilare le seguenti tre tabelle con dati sperimentali e mostrarle al docente.

Tabella 1.

0 = 10 о
numero di misura	serie 1		serie 2		serie 3		serie 4		Episodio 5

Tavolo 2.

0 = 20 о
numero di misura	serie 1		serie 2		serie 3		serie 4		Episodio 5

Tabella 3.

0 = 30 о
numero di misura	serie 1		serie 2		serie 3		serie 4		Episodio 5

Quando si misura la lunghezza io del pendolo, va tenuto presente che quest'ultimo è costituito dalla lunghezza del filo che trattiene la sfera e dal raggio della sfera.

Il raggio della sfera viene calcolato attraverso il suo diametro, che viene misurato con un calibro a corsoio. Poiché la sfera non rappresenta una superficie sferica ideale, ogni misurazione del diametro darà un valore leggermente diverso da quello misurato in precedenza.

Il dispositivo, che attua i movimenti oscillatori del pendolo, ha un dispositivo che regola la lunghezza del filo. In questo caso, la lunghezza del filo può essere misurata in due modi: o applicare un filo di riferimento al filo di lunghezza fissa, la cui lunghezza deve poi essere misurata su un righello di misurazione; oppure prendi un filo di una certa lunghezza come filo di riferimento e fissa la lunghezza del filo del pendolo con l'aiuto di un dispositivo regolabile di questo dispositivo.

La piattaforma mobile (vedi Fig. 1) permette di misurare la lunghezza del pendolo in un altro modo. Per fare ciò, è necessario combinare il filo del pendolo insieme alla palla con il piano superiore della piattaforma mobile (vedi Fig. 3) La stessa posizione della piattaforma può essere fissata sul righello di misurazione - questo sarà la lunghezza del filo insieme alla sfera, dalla quale deve essere sottratto il raggio della sfera. Il diametro della sfera deve essere misurato con un calibro a corsoio.

Riso. 3.

Periodo T le oscillazioni del pendolo sono meglio definite come segue: misurare il tempo T diverse oscillazioni del pendolo e poi dividere questo tempo per il numero di oscillazioni. Va tenuto presente che il tempo di un'oscillazione indica il tempo durante il quale la palla ritorna da una delle posizioni estreme alla stessa posizione.

Per impostare l'angolo richiestoφ 0 è necessario utilizzare una piastra metallica rettangolare, sulla quale emergono più linee guida da un punto, inclinate con angoli diversi rispetto alla linea verticale che emana da questo punto. Questi angoli possono essere misurati con un goniometro.

La piattaforma mobile consente alla piastra rettangolare di allinearsi con il punto di sospensione del filo del pendolo in modo che la linea verticale sulla piastra coincida con il filo del pendolo quando la sfera è in posizione abbassata.

Dopo questo allineamento, la piattaforma mobile insieme alla piastra può essere fissata. Ora, quando il filo viene deviato in uno o nell'altro angolo, deve essere allineato con una delle linee della piastra che definisce un angolo specifico (vedi Fig. 1)

IV ... Elaborazione dei risultati di misurazione

Uno qualsiasi dei valori misurati l e T presentati nelle tabelle 1-3 non sono valori esatti, poiché sono misurati con alcuni errori.

In tali casi, le medie aritmetiche calcolate dalle formule (14) sono prese come i valori esatti delle quantità indicate. Quindi, per errore di misurazione, intendiamo il modulo della deviazione massima di tutti i valori misurati dalla loro media aritmetica. Vale a dire, l'errore ∆ 1 le misure della lunghezza del pendolo saranno definite come

1 = massimo | l io - l cfr |, (15)

e l'errore ∆ 2 - il periodo di oscillazione del pendolo va calcolato come segue:

2 = massimo | T i - T av | ... (16)

Nelle formule (15) - (16) l'indice io = 1,2,3… scorre attraverso tutti i numeri di misura delle grandezze corrispondenti.

Elaboreremo i risultati della misurazione su un computer nel programma Microsoft Excel e dimostreremo la tecnologia dei calcoli necessari sulla base di risultati di misurazione specifici.

Si riempia la tabella 3 con i seguenti dati effettivi.

Tabella 3

0 = 30 о
numero di misura	serie 1		serie 2		serie 3		serie 4		Episodio 5
	0,505 0,495 0,503 0,498 0,500	1,434 1,434 1,428 1,422 1,418	0,606 0,594 0,603 0,597 0,600	1,547 1,553 1,557 1,575 1,553	0,704 0,696 0,702 0,698 0,700	1,685 1,681 1,678 1,691 1,687	0,806 0,794 0,804 0,797 0,800	1,807 1,815 1,791 1,791 1,800	0,904 0,896 0,903 0,898 0,900	1,907 1,909 1,925 1,906 1,897

Per ogni serie di misure è necessario calcolare con formule (14) l av e T av e poi costruisci la dipendenza T cf 2 = f (l cf) ... Per comodità introduciamo la seguente notazione: T cf 2 = y 1, l cf = x 1.

Prima di procedere ai calcoli indicati, costruiamo nel programma Eccellere tabella 3 e preparare il formato della tabella 4, i cui dati verranno utilizzati durante la costruzione della dipendenza funzionale y 1 = f (x 1).

In Excel La tabella 3 è formata come segue.

Sul Foglio1 della cartella di lavoro Eccellere attivare una serie di cellule cell A 1: A 2, uniscili e inserisci il titolo della prima colonna nella cella unita risultante dalla tastiera: " n numero di misura", Attiva l'intervallo di celle SI 1: DO 1, uniscili e inserisci l'intestazione comune della seconda e della terza colonna nella cella unita risultante dalla tastiera: " serie 1 ", Attiva la cella B 2 e inserisci da tastiera il sottotitolo della seconda colonna della Tabella 3: “ io "Dopodiché, attiviamo la cella C2 e inseriamo il sottotitolo della terza colonna della Tabella 3 dalla tastiera:" T ". Ripetiamo le azioni indicate per le restanti colonne della Tabella 3. Come risultato dell'esecuzione delle azioni precedenti, otteniamo il formato della Tabella 3.

Ora riempiamo il formato risultante con i dati della tabella 3, a seguito della quale otteniamo la tabella 3 nel programma Eccellere.

Per costruire il formato della tabella 4 nel programma Eccellere sul Foglio1 della cartella di lavoro Eccellere attiva la cellula UN 9 e inserisci da tastiera l'intestazione della prima colonna: “ n B 9 e inserisci l'intestazione della seconda colonna dalla tastiera: " l cf = x 1 ". Allo stesso modo, inseriamo le intestazioni della terza, quarta e quinta colonna dalla tastiera: " T cf "," T cf 2 = y 1 "e" y 1 / x 1 "nelle celle C 1, D 1 ed E 1 rispettivamente. Successivamente, attiviamo la cella UN 10 e inserisci il numero 1 dalla tastiera, nella cella UN 11 cifra 2, attiva l'intervallo di celle LA 10: LA 11 e completamento automatico alla cella UN 14. Come risultato dell'esecuzione delle azioni di cui sopra, otteniamo la tabella 4.

Tabella 4.

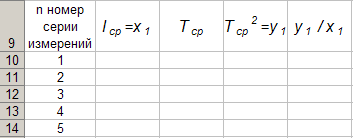
Dimostreremo la tecnologia di riempimento della prima riga della Tabella 4 elaborando le misurazioni della serie 1.

Per cui programmiamo la prima formula in (14), otteniamo l mer e mettilo nella tabella 4. B 10 e digita la formula "= SOMMA (B3: B7) * (1/5)" da tastiera.

Quindi programmiamo la seconda formula in (14). E 2 e digita la formula "= SOMMA (C3: C7) * (1/5)" dalla tastiera.

Otteniamo T av e al quadrato, quindi calcolare il rapporto. Per fare ciò, attiva la cella D 10 e digita la formula "= C10^2" dalla tastiera, quindi attiva la cella E 10 e digita la formula "= D10 / B10" da tastiera. Dopo tutte queste azioni, la prima riga della tabella 4 assume la forma

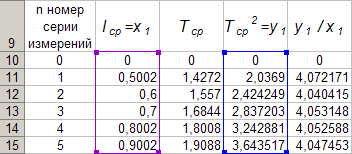
Dopo aver ripetuto i calcoli precedenti per altre serie, la tabella 4 assume la forma finale

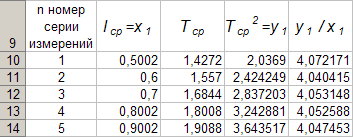
I dati in Tabella 4 consentono l'utilizzo del programma Eccellere costruire un grafico di dipendenza funzionale y 1 = f (x 1).

Per fare ciò, attiva l'intervallo di celle RE 10: RE 14, chiamiamo la procedura guidata delle funzioni del programma Eccellere , seleziona il tipo di grafico "Dispersione", la prima visualizzazione. Spostare il cursore del mouse sul pulsante "Avanti" ed eseguire un singolo clic del pulsante sinistro del mouse (LMB). Successivamente, vai alla scheda Riga. Per fare ciò, sposta il cursore del mouse sulla scheda "Riga" situata nella parte superiore della finestra "Procedura guidata grafico" ed esegui un singolo clic LMB. Quindi, posiziona il cursore nel campo "X Values" e quindi sposta il cursore del mouse sulla cella B 10, premi LMB e senza rilasciarlo sposta il cursore del mouse sulla cella B 14 quindi rilasciare LMB. Di conseguenza, la formula "= Foglio1! $ B $ 10: $ B $ 14 ". Ora sposta il cursore del mouse sul pulsante "Avanti" ed esegui due clic LMB di seguito, quindi sposta il cursore del mouse sul pulsante "Fine" ed esegui un singolo clic LMB. Sul Foglio1 della cartella di lavoro Eccellere apparirà un grafico della dipendenza funzionale y 1 = f (x 1) ... Attiviamo la riga 10 e aggiungiamo una nuova riga, dopodiché entriamo dalla tastiera nelle celle A 10: E 10 cifre "0". Quindi, sposta il cursore del mouse in qualsiasi punto del grafico ed esegui un singolo clic LMB. Aumentiamo l'intervallo di dati del grafico, per il quale spostiamo il cursore del mouse sul bordo dell'intervallo di valori e 1 e sposta l'indicatore situato nell'angolo in alto a destra del bordo nella cella D 10. Facciamo lo stesso con la gamma x 1.

Ora sposta il cursore del mouse su un punto qualsiasi del grafico ed esegui un singolo clic con il pulsante destro del mouse (RMB). Nel menu contestuale che appare, sposta il cursore del mouse sul comando "Aggiungi linea di tendenza" ed esegui un singolo clic LMB. La Figura 4 illustra il risultato di queste costruzioni.

Figura 4.

La figura 4 implica che la dipendenza y 1 = f (x 1) è lineare ed è descritto dall'equazione

y 1 = 4,04 8 x 1 + 0,00 24 (17)

L'equazione 17 mostra che la pendenza K dall'equazione (10) risulta essere uguale a: K = 4.0493. Se questo valore K sostituito nella formula (12), si ottiene il valore dell'accelerazione di gravità.

Pendenza K nell'equazione (10) può essere calcolato dai dati nella tabella 4 dalla formula

(18)

Per fare ciò, attiva la cella UN 17 e inserire la formula “= SOMMA ( MI 11: MI 15) * (1/5) "

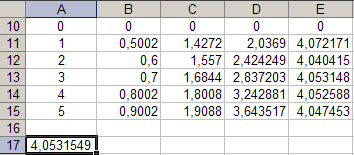
otteniamo k = 4.053, cioè numero vicino al numero K ottenuto dal grafico mostrato in Figura 4.

Ovviamente, il numero ottenuto dalla formula (12) utilizzando la quantità K dall'equazione (17) avrà qualche errore.

Per calcolare questo errore, torniamo ai dati nelle Tabelle 3 e 4.

Primo nel programma Eccellere creare un formato per una nuova tabella 5. Perché sul Foglio1 della cartella di lavoro Eccellere attiva la cellula UN 19 e inserisci da tastiera l'intestazione della prima colonna: “ n numero della serie di misure ", attivare la cella B 19 e inserire la seconda colonna intitolata da tastiera: “∆ 1 secondo (15)”. Allo stesso modo, inserisci le intestazioni della terza colonna dalla tastiera: “∆ 2 per (16) "nella cella C 19. Quindi, attiva la cella UN 20 e inseriscici il numero 1 dalla tastiera, nella cella UN 21 cifra 2, attiva l'intervallo di celle LA 20: LA 21 e completamento automatico alla cella UN 26. Come risultato dell'esecuzione delle azioni di cui sopra, otteniamo la tabella 5.

Tabella 5.

Quando si programmano le formule (15) e (16), è necessario io e T io , per ogni serie di misurazioni ricavate dalla Tabella 3, e l av e T av dai dati della tabella 4.

Per calcolare 1 per la prima serie di misure è necessario attivare la cella m 3 e inserisci la formula "= ABS (B3-B $ 11))" dalla tastiera, quindi completeremo automaticamente la cella m 7. Ora nella cella B 20 inseriremo da tastiera la formula "= MAX (M3: M7)".

Per calcolare 2 secondo i dati della stessa serie, è necessario attivare la cella n 3 e inserisci la formula "= ABS (C3-C $ 11)" dalla tastiera, dopodiché completeremo automaticamente la cella n 7. Ora nella cella C 20 inseriremo da tastiera la formula "= MAX (N3: N7)".

Di conseguenza, la tabella 5 assume la forma

Dopo aver eseguito i calcoli secondo (15) e (16) per i dati di altre serie di misurazioni, la Tabella 5 assume la forma

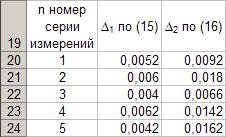
Dai dati in Tabella 5, è ovvio che per ogni serie di misurazioni i valori esatti della lunghezza io pendolo e periodo T le oscillazioni del pendolo sono definite come segue

l = l av ± ∆ 1, T = T av ± ∆ 2 (19)

Inoltre, si scopre che ∆ 1 e ∆ 2 sono differenti per ciascuna delle lunghezze del pendolo. Dalle formule (19) segue che la retta in Fig. 4 è disegnata con un errore e nelle sue vicinanze c'è una cosiddetta dispersione di dati sperimentali.

Per tenere conto della dispersione dei dati sperimentali, calcoliamo altre due dipendenze funzionali:

(T media + ∆ 2) 2 = f (l av + ∆ 1), (20)

(T av - ∆ 2) 2 = f (l av - ∆ 1). (21)

Per calcolare la dipendenza (20), introduciamo nuove designazioni:

x 2 = (l cf + ∆ 1), (22)

y 2 = (T media + ∆ 2) 2, (23)

Prima di procedere con i calcoli utilizzando le formule (22) e (23), formiamo il formato di una nuova tabella 6 utilizzando il programma Eccellere , secondo l'algoritmo precedentemente indicato, allora otteniamo

Tabella 6.

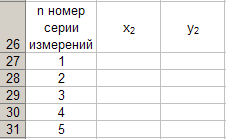
Quando si calcola x 2 e y 2 secondo (22) e (23), è necessario utilizzare i dati nelle Tabelle 4 e 5. Innanzitutto, calcoliamo x 2 e i numeri risultanti sono inseriti nella tabella 6.

Per fare ciò, attiva la cella B 27 e inserisci da tastiera la formula "= B11 + B20".

Quindi calcola y 2 per questo attiviamo la cellula C 27 e digita la formula "= (C11 + C20) ^ 2" dalla tastiera.

SI 27: DO 27 e completamento automatico alla cella C31.

Quindi la tabella 6 sarà riempita con i seguenti dati

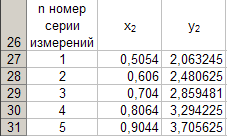
Secondo la tabella 6, costruiamo un grafico di dipendenza y2 = y2 (x2) (vedi Fig. 5) secondo la tecnologia precedentemente descritta

La figura 5 mostra che la dipendenza y2 = y2 (x2) è determinato dall'equazione

y2 = 4,08 86 x 2 - 0,002 3 (24)

Procediamo al calcolo della dipendenza funzionale (21). Per questo, introduciamo due formule ausiliarie

x 3 = l cf - ∆ 1, (25)

y 3 = (T av - ∆ 2) 2. (26)

Il calcolo secondo queste formule viene effettuato secondo i dati delle tabelle 4 e 5 e i risultati di questi calcoli sono inseriti nella tabella 7. Innanzitutto, calcoliamo x 3 ... Per fare ciò, attiva la cella B 34 e inserisci da tastiera la formula "= B11-B20".

Quindi calcola y 3 per questo attiviamo la cellula C 34 e inserisci la formula "= (C11-C20) ^ 2" dalla tastiera.

Ora attiviamo l'intervallo di celle. Si 34: Do 34 e completamento automatico alla cella C 38.

I dati in questa tabella sono i seguenti

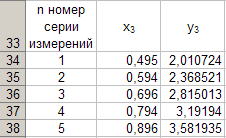
Dipendenza funzionale sì 3 = sì3 (X3 ) , costruito secondo i dati in Tabella 7 è mostrato in Figura 6.

La figura 6 implica che

sì3 = 4,00 7 3 X3 + 0,00 71 (27)

Valori di pendenzaKsecondo i dati delle equazioni (17), (24), (27) entriamo nella tabella 8.

Programmiamo la formula (12) e calcoliamoGcorrispondente a ciascun valoreK... Inseriamo i valori ottenutiGnella tabella 8. Per fare ciò, attiva la cellaC41 e digita la formula "= (4 * PI () ^ 2) / B41" dalla tastiera. Dopodiché, completeremo automaticamente la cellaC43.

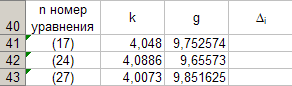
Adesso calcoliamo la mediaGsecondo la formula

Per fare ciò, attiva la cellaC45 e inserisci la formula "= (1/3) * SUM (C41: C43)" dalla tastiera.

Risulta essere uguale a 9,75331, che prendiamo come valore esatto. L'errore nel determinare questo valoreGcalcolato dalla formula

Δ 3 = max | Gio – Gmer| = max | Δ io| (28)

Per fare ciò, attiva la cellaD41 e inserisci la formula "= ABS (C41-C $ 45)" dalla tastiera. Dopodiché, completeremo automaticamente la cellaD43.

calcoliamoΔ ioe mettilo nella tabella 8. Per fare ciò, attiva la cellaD45 e digitare da tastiera la formula "= MAX (D41: D43)".

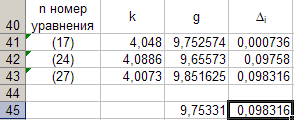
Dai dati della Tabella 8 segue cheΔ 3 = 0,098316. Quindi l'accelerazioneGla caduta libera ottenuta con questo dispositivo, a seguito di misurazioni indirette, è risultata essere

g = 9,7533 ± 0,0983.

Domande di controllo

1. Quali sono gli elementi del dispositivo per studiare le oscillazioni di un pendolo matematico.
2. In base a quale legge della meccanica viene compilata l'equazione del moto del pendolo.
3. Quali sono i vincoli sotto i quali si ottiene un'equazione che simula il movimento di un pendolo matematico.
4. Quali vibrazioni sono chiamate armoniche.
5. Dare una definizione dell'ampiezza, della fase e della frequenza delle oscillazioni.