Keermependli võnkumiste uurimine ja mõõtmine. Füüsika laboratoorne töö "matemaatilise pendli seaduste uurimine"

Laboratoorne töö

Matemaatilise pendli seaduste uurimine

Eesmärk: Uurige matemaatilise pendli seadusi ja määrake raskuskiirendus

Varustus: Pendel (pall vedrustusel), joonlaud, stopper või kell teise käega.

Lühike teooria:

Matemaatiline pendel on ostsillaator, mis on mehaaniline süsteem, mis koosneb materiaalsest punktist, mis paikneb raskusteta venitamatul niidil või kaaluta vardal gravitatsioonijõudude homogeensel väljal.

Pendli pikkus l on kaugus riputuspunktist kuuli raskuskeskmeni.

Võnkeperioodi praktiliseks arvutamiseks kasutage valemit:

,

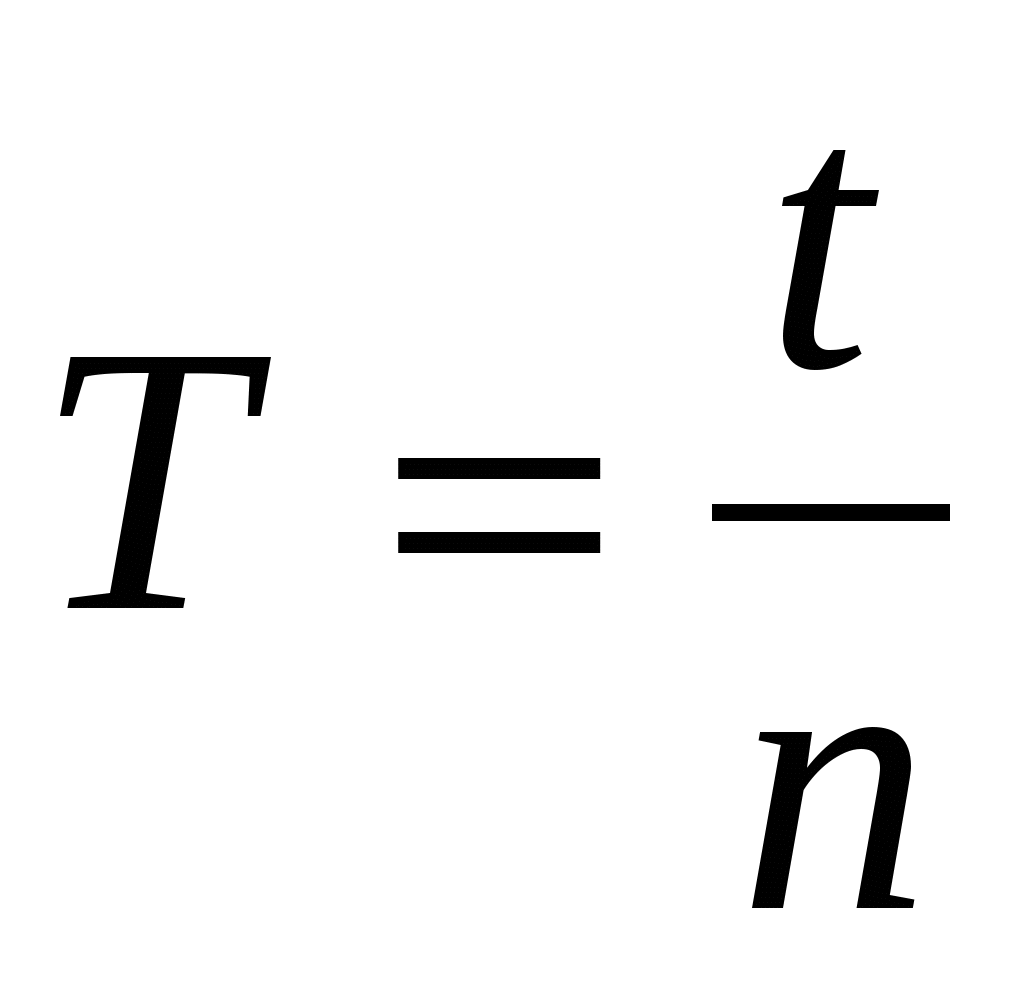kus T on võnkeperiood,

t - võnkeaeg,

n on täielike vibratsioonide arv.

Vastavalt võnkumisseadustele saab pendli perioodi määrata valemiga:

,

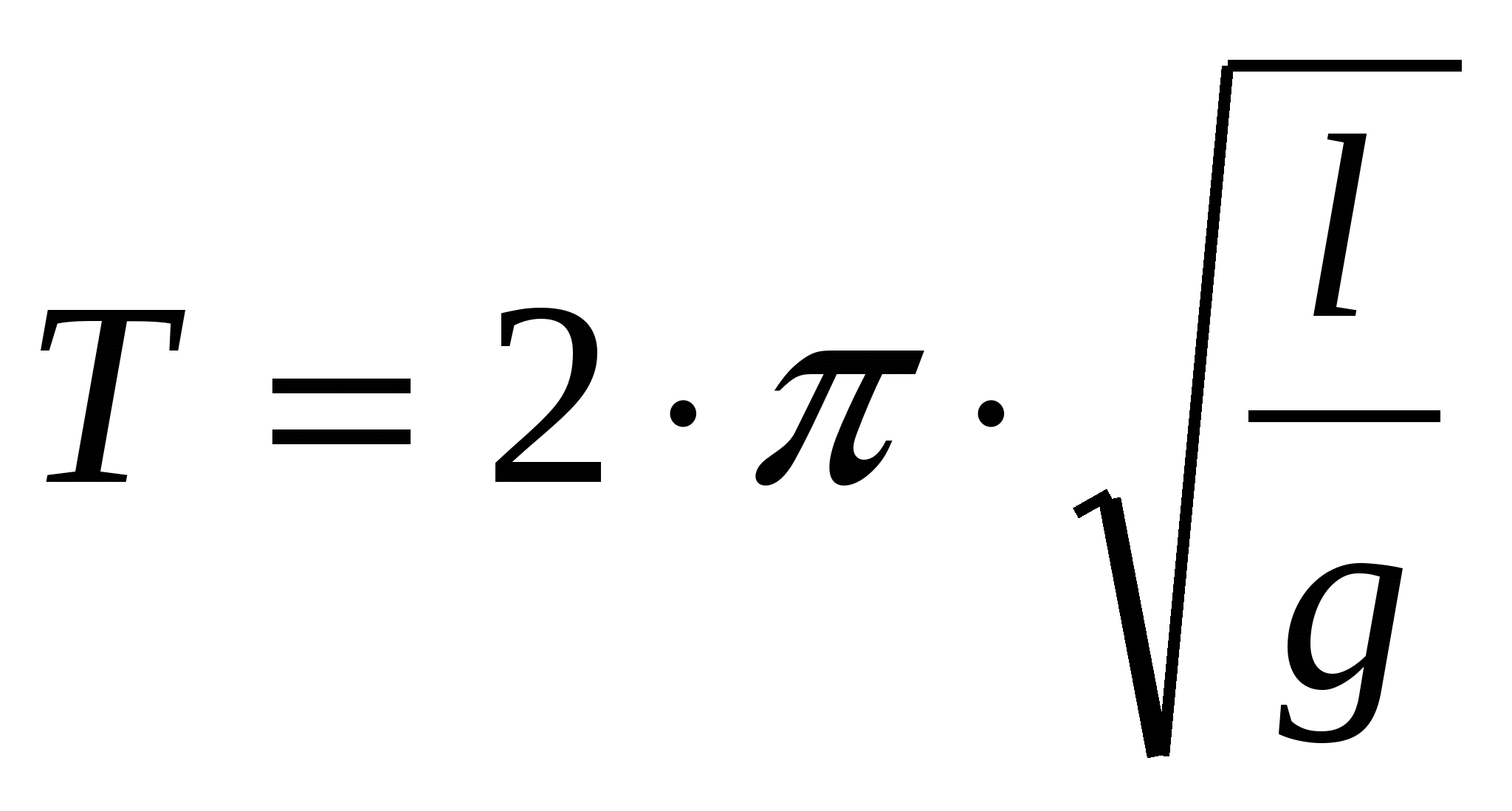Matemaatilise pendli võnkeperiood ei sõltu palli massist.

P matemaatilise pendli võnkeperiood on otseselt proportsionaalne pendli pikkusega ja pöördvõrdeline raskuskiirendusega. Seda võrrandit nimetatakse Huügensi valemiks.

Ajalooline viide

Christian Huygens van Zuilichem (14. aprill 1629 - 8. juuli 1695). Hollandi füüsik, matemaatik, mehaanik ja astronoom ning leiutaja. Sündinud Haagis. Ta õppis Leideni ülikoolis õigusteadust, kuid ei lõpetanud matemaatika õppimist. Galileo uuringute põhjal lahendas ta mitmeid mehaanika probleeme. Aastal 1656 konstrueeris ta 27-aastaselt esimese põgenemispendli kella. Kella loomisel, mis mõõtis aega selleks ajaks enneolematu täpsusega, olid kaugeleulatuvad tagajärjed füüsilise katse ja inimese praktilise tegevuse arengule. Enne seda mõõdeti ju aega vee väljavoolu, tõrviku või küünla põlemise järgi. Huygensi poolt 1673. aastaks loodud võnketeooria oli hilisema valguse olemuse mõistmise alus.

Huygensi valemi põhjal saame matemaatiliste teisenduste abil avaldumise raskuskiirenduseks:

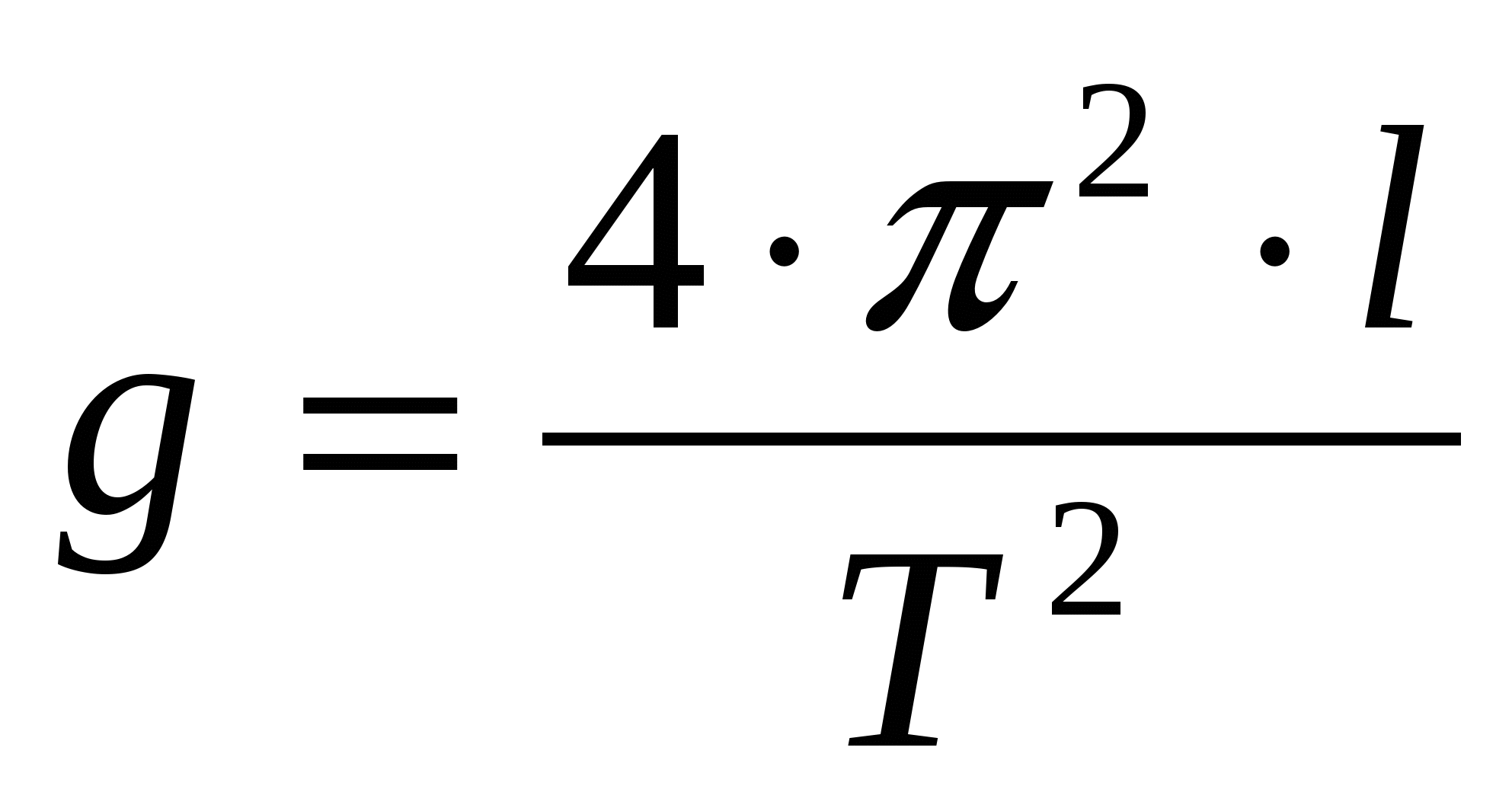
Meie katsetes on matemaatilise pendli tegelik mudel väike õhukesele elastsele niidile riputatud pall. Palli suurus peaks olema keerme pikkusega võrreldes väike. See võimaldab eeldada, et kogu mass on koondunud ühte punkti, kuuli raskuskeskmesse.

Tööprotsess:

Määrake seadmete jagunemishind:

joonlaud …… ..m / div.

stopper …… .s / div.

2. Määrake instrumentide viga (instrumentide absoluutne viga võrdub skaalaintervalliga ½):

valitseja Δ l = …… ..m

stopper Δ t \u003d ……. S

Määrake pendli maksimaalne pikkus ja mõõtke see l 1 \u003d… m.

Käivitage pendel (läbipaindenurk 10-15 0) ja õigeaegselt t loe vibratsioonide arv n (vähemalt 7).

Vibratsioonide arvu muutmisega korrake katset veel 3 korda.

t 2 \u003d ………, n 2 \u003d …………. T 2 \u003d ………,

t 3 \u003d ………, n 3 \u003d …………. T 3 \u003d ………,

t 4 \u003d ………, n 4 \u003d …………. T 4 \u003d ………,

Muutke pendli pikkust l 2 \u003d… .m ja korrake kõiki mõõtmisi.

Sisestage andmed tabelisse.

№ mõõdud

Pendli pikkus

l, m

№ kogemus

Võnkumise aeg,

t, s

Vibratsioonide arv

n

Võnkeperiood,

T, s

Perioodi keskmine väärtus, T avg, s

Vabalangemise kiirendus, g, m / s 2.

Tähendab

vabalangemise kiirendus, g keskmine, m / s 2.

l vrd \u003d

t K \u003d

suhteline: absoluutne:

,

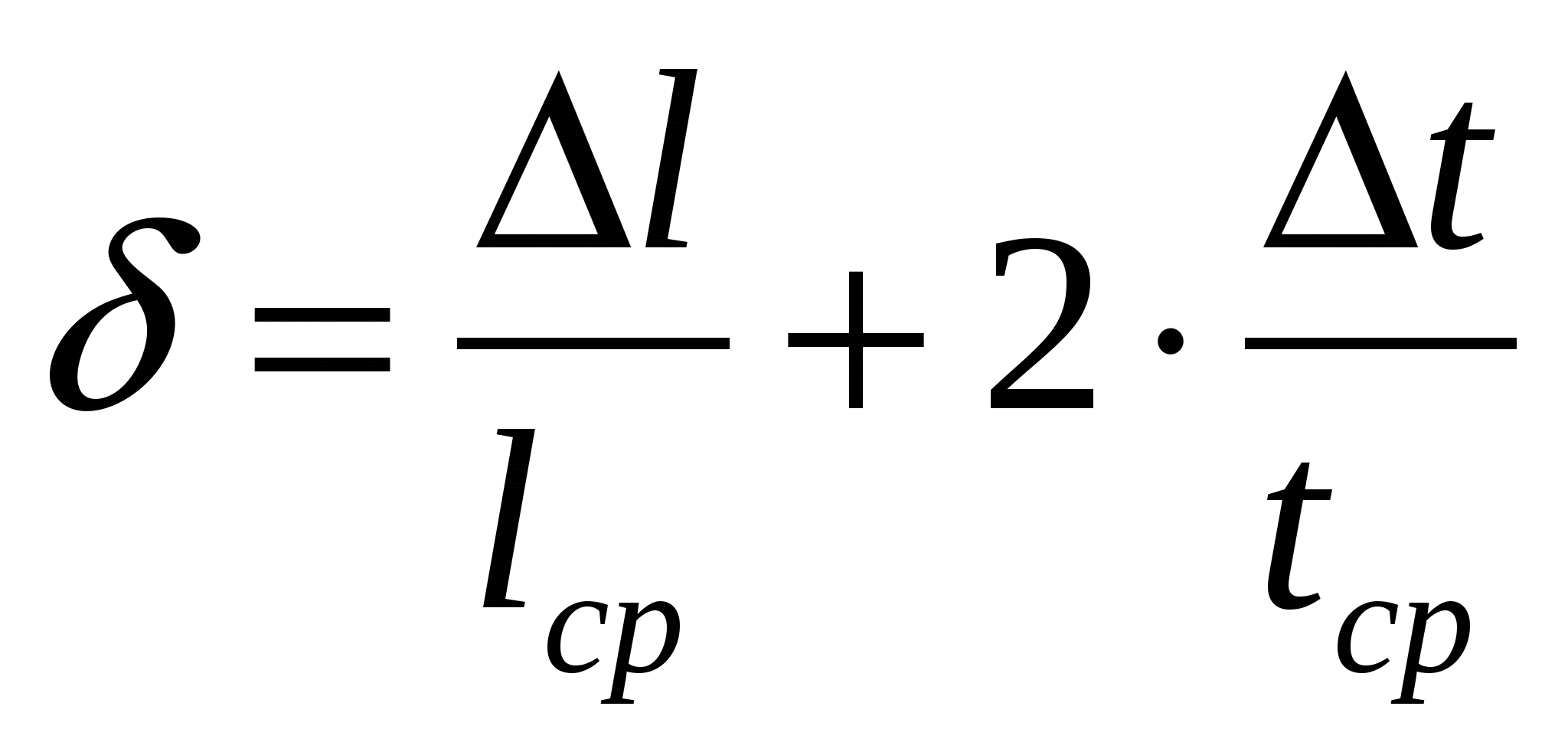
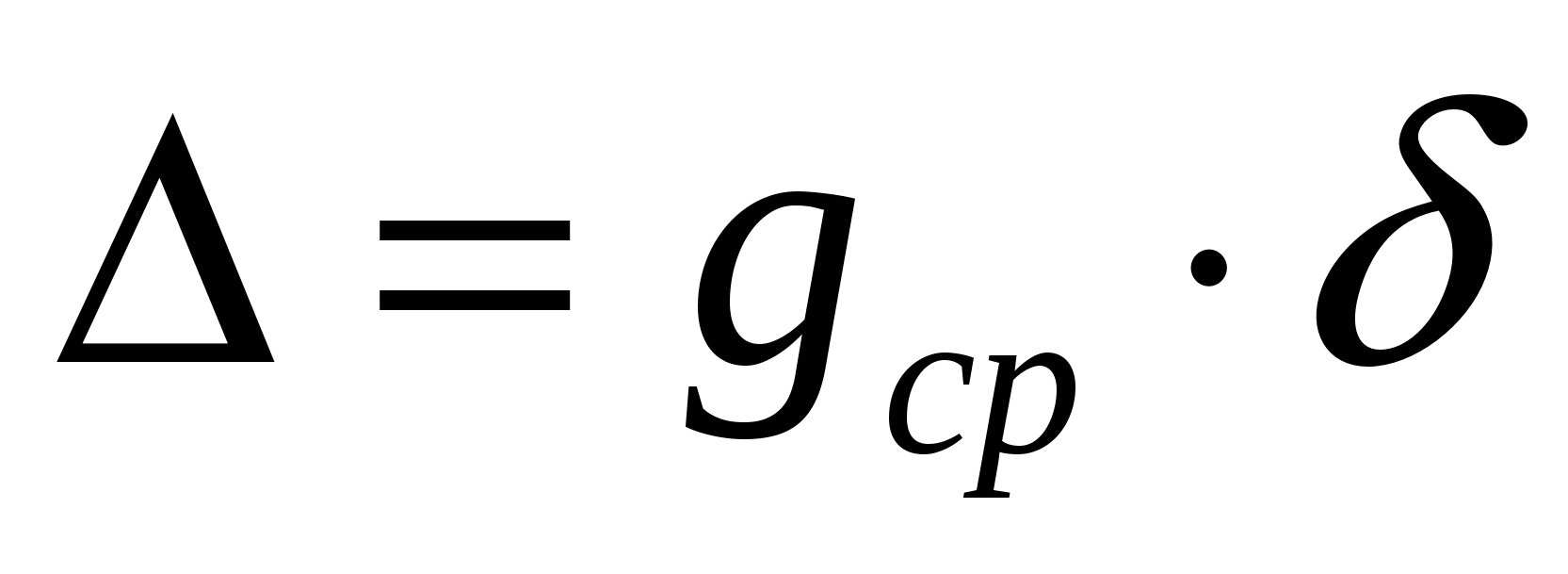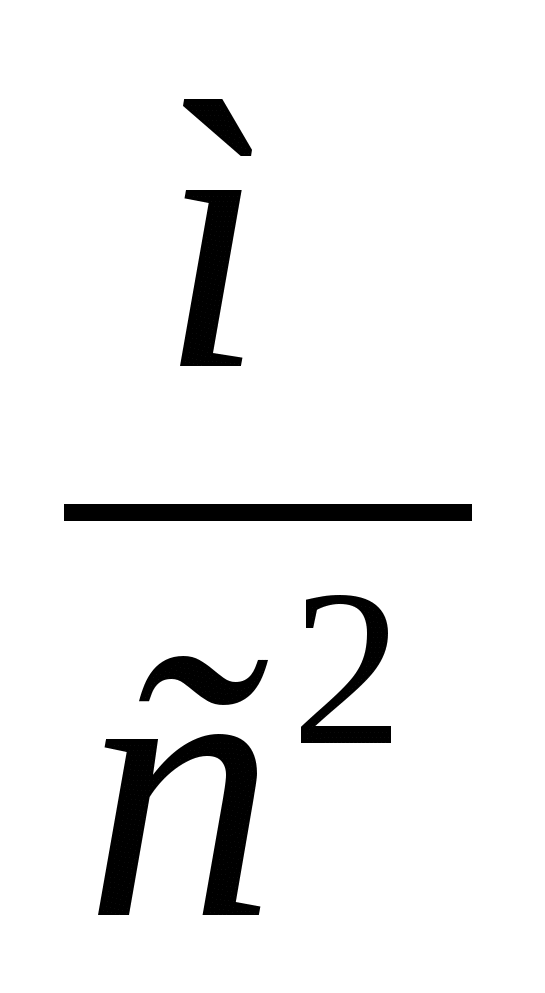
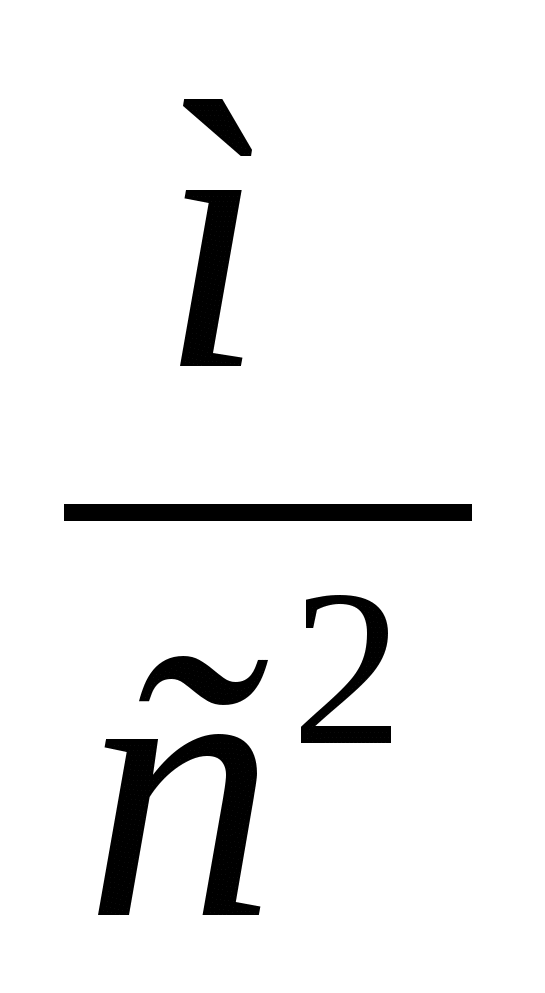
Testküsimused:

Kui pikk on matemaatiline pendel, mille periood on 2 s?

Leidke massi mass, mis 250 N / m jäikusega vedrul tekitab 16 sekundi jooksul 20 vibratsiooni.

Raskuskiirendus Kuul on 1,7 m / s 2. Mis saab olema Kuu matemaatilise pendli võnkumise periood, kui Maal on see võrdne 1 s-ga? Kas vastus sõltub veose kaalust?

Võnkuva keha koordinaat muutub vastavalt seadusele x \u003d 0,5sin 45πt. Mis on võnkumiste amplituud ja periood?

Punkti pidevate võnkumiste amplituud on 12 cm, lineaarne sagedus on 14 Hz, võnkumiste algfaas on 0. Kirjutage punkti x \u003d x (t) liikumisvõrrand.

Skaala jaotus

Väärtuste erinevus (ilma märgita) füüsiline kogusvastab jagunemist piiravatele skaalamärkidele. Digitaalseadmetes toimib diskreetsuse aste skaalajaotuse väärtust asendavana.

a) valige skaalalt kaks lähimat digiteeritud joont;

c) väärtuste erinevus (lahuta suuremast väiksem) jagage valitud löökide korral jagunemiste arvuga.

H

see joonis näitab termomeetri skaalat suures ulatuses. Kasutame seda jagunemishinna arvutamise reegli illustreerimiseks.

a) valige digiteeritud jooned 20 ° С ja 40 ° С

b) 10 jaotust (tühikut) nende vahel

c) arvutage: (40 ° С - 20 ° С): 10 jaotust \u003d 2 ° С / div.

Vastus: jagunemiste hind \u003d 2 ° С / div,

Digitaalseadmetel pole selgesõnaliselt skaalat ja jagamishinna asemel on neile märgitud seadme näitusel numbri kõige vähem olulise numbri ühiku hind.

P


näide:

1) selle seadme skaalajaotuse hind on 1 (tavapärased ühikud) / div.

2
) selle seadme skaalajaotus on 0,01 (tavapärased ühikud) / div.

3
) selle seadme skaalajaotus on 0,1 (tavapärased ühikud) / div.

4) selle seadme skaalajaotus on 0,001 (tavapärased ühikud) / div.

Mina Eesmärk

Vaatlused matemaatilise pendli võnkeliikumistest, mis on rakendatud seadmel, mille funktsionaalne skeem on näidatud joonisel 1.

Pendli võnkeperioodi mõõtmine erineva pikkuse ja amplituudiga.

Matemaatilise pendli võnkumiste isokronismirežiimi määramine.

Palli gravitatsioonikiirenduse arvutamine kindlaksmääratud mõõtmistulemuste põhjal.

II ... Teoreetiline osa

Vaatleme seadet, mis koosneb väikesest pallist, mis on kinnitatud suspensiooni fikseeritud punkti külge, kasutades teatud pikkusega kaalutut venitamatut niiti (joonis 1).

Kui palli suurus on palju väiksem kui pikkusl niidid, siis saab palli näha kui materiaalne punkt; ja kui palli mass on palju suurem kui niidi mass, siis viimast võib pidada kaalutuks. Keermet võib pidada ka pikendamatuks tingimusel, et kuuli raskusjõud põhjustab lõime lõpmatult väikese pikenemise.

See seade võimaldab teil simuleerida nn matemaatilise pendli võnkumist.

Joonis: 1. Seade matemaatilise pendli võnkumiste uurimiseks: 1. metallplaat pendli läbipainde nurga seadmiseks; 2. teisaldatav platvorm; 3. Joonlaua mõõtmine.

Joonis 2. Matemaatilise pendli võnkuvate liikumiste illustratsioon.

Esialgses olekus on niit suunatud vertikaalselt allapoole (joonisel 2 asend 1). Sel juhul tugevusF niidi pinge ja tugevusmg palli raskused langevad kokku lõime suunaga, kuid on suunatud vastupidiselt. Kuna niit on pikendamatu, tasakaalustavad mõlemad jõud üksteist, s.t.F \u003d mg ... Pall on puhkeasendis. Seda pendli olekut nimetatakse selle tasakaalupositsiooniks.

Võtame pendli tasakaaluasendist välja, suunates palli algseisundist nurga allaφ 0 (joonis 2). Lase siis sellest lahti surumata. Gravitatsiooni järgimg pall hakkab liikuma tasakaaluasendi suunas, mõne aja pärast möödub sellest, siis teisel pool tasakaaluasendit kaldub ta sellest mõne nurga all vähem kuiφ 0 ja gravitatsiooni mõjul kihutab jälle tasakaaluasendi poole. Pallile väliste mõjude puudumisel sooritab viimane kirjeldatud liikumise ühes tasapinnas. Ilmselt on palli trajektooriks ringikujuline raadiusega kaarl ... Neid liikumisi nimetatakse vibratsiooniks.

Pallile mõjuva takistusjõu mõjul sumbuvad selle võnkumised, mida tõendab asjaolu, et pärast iga tasakaalu möödumist kaldub see sellest üha väiksema nurga all. Kui aga seda protsessi täheldatakse üsna lühikest aega, siis võnkeprotsessi võib tunnistada pidevana.

Vaatleme suvalisel hetkel pallile mõjuvaid jõudet. Olgu φ - keerme läbipainde nurk sel hetkel. Kirjutame suuna järgmise Newtoni teise seaduse võrrandiτ , mis langeb kokku puutujaga, mis on tõmmatud palli trajektoori punktile, milles see asub vaadeldaval ajahetkelt.

ma τ \u003d - mg sin φ (1)

Siin a τ - tangentsiaalne kiirendus,m Kas palli mass. Parempoolne miinusmärk punktis 1 võtab arvesse asjaolu, et tasakaaluasendist ülespoole liikudes takistab raskusjõud seda liikumist.

Palli nurkkiirendus ε on määratletud kui nurga teine \u200b\u200bajaderivaatφ, s.t.

. (2)

Tangentsiaalse kiirenduse vahela τ ja nurga all ε on ilmne seos

(3)

Valemit (2) ja (3) arvesse võttes on võrrand (1) järgmine:

. (4)

Võrrandis (4) on tundmatu funktsioonφ (t) seisab teise järgu tuletise märgi all. Sellist matemaatika võrrandit nimetatakse teise järgu tavaliseks diferentsiaalvõrrandiks.

Seda saab lihtsustada, kui võtame seda arvesse väikeste nurkade allφ, mõõdetuna radiaanides. Siis (4) asemel saame

. (5)

Võrrand (5) kirjeldab pendli liikumist. Seda nimetatakse ka harmoonilise ostsillaatori võrrandiks.

Otsese asendamise abil saab kontrollida, kas võrrandi (5) lahendus on vormis

, (6)

kui tähistame

. (7)

Seega on näha, et nurk muutubφ ajas toimub sinusoidse seaduse järgi. Kogusφ 0 , võrdset maksimaalse kõrvalekaldenurgaga tasakaaluasendist nimetatakse harmooniliste vibratsioonide amplituudiks. Amplituudi suurus sõltub sel juhul algsest kõrvalekaldest. Siinusmärgi all olevat väärtust nimetatakse faasiks. Faas kasvab aja järgi. Siinusmärgi all olevat väärtust nimetatakse algfaasiks, mis on vaadeldavas liikumises null.

Siinusfunktsioon, mis määrab võnkumisliigutuste olemuse, on perioodiline funktsioon, mille periood on võrdne. Viimane tähendab, et kui pärastT määrake pendli võnkeperiood, siis saame faasi väärtuseks kirjutada järgmise võrdsuse

, (8)

kus on ümmargune sagedus.

Võttes nüüd arvesse perioodi (7)Me saame:

(9)

Seos (9) näitab, et võrrandi (4) lineariseerimine viis võrrandini (5), mille lahendus lubab sõltumatustT amplituudil φ 0.

Selliseid kõikumisi nimetatakse isokroonseteks.

Valemit (9) saab esitada ka järgmiselt:

k l, (10)

kust läbi

(11)

funktsiooni lineaarse funktsionaalse sõltuvuse kalleT 2 argumendist l.

Järelikult kontrollitakse pendli võnkumiste isokronismi suhte (10) kehtivusega vastavalt perioodi mõõdetud väärtusteleT erinevatel väärtustell sama nurga allφ 0 .

Katsepunktidest konstrueeritud funktsionaalne sõltuvus võimaldab määrata kallek, mille arvväärtuse kaudu kiirendusg palli vaba kukkumine arvutatakse järgmiselt:

. (12)

Lisaks üksikute mõõtmiste abilT ja l kiirendus g saab arvutada ka selle suhte põhjal:

(13)

III ... Katse protseduur

Kuna võrrandi (4) lineariseerimine, mis viis võrrandini (5), mis kirjeldab isokroonseid võnkeid, põhineb eeldusel, on ilmne, et isokroonse vahemiku määravad nurga väärtusedφ 0 mille korral on lineaarne sõltuvus.

Seega määratleda väärtuste vahemikφ 0 , mille puhul seos (10) kehtib, on see vajalik mitme väärtuse jaoksφ 0 tehke mõõtmised, mis võimaldavad teil luua sõltuvusi, siis arvutage määratud funktsionaalsete sõltuvuste põhjal kallek ja valitud nurkade jaoksφ 0 arvutage väärtusedg vastavalt punktile 12 ja võrrelda neid üldtunnustatud väärtusegag \u003d 9,8 m / s 2. Need nurgad φ 0 mille jaoks arvutatud väärtusg mõõtmisviga arvesse võttes salvestab see samad arvväärtused ja määrab selle seadme realiseeritud võnkumiste isokronismivahemiku.

Mõõtmiste järjekord on järgmine: valitakse konkreetne nurga väärtusφ 0 , mille abil on vaja pall tasakaalupositsioonilt kõrvale juhtida, seatakse pendli pikkus, viiakse läbi katse, mille jooksul mõõdetakse perioodT ... Katse viiakse läbi mitu korda, nii et fikseeritud nurga allφ 0 mõõdetud väärtusi peab olema kolm kuni viisl ja T.

See on esimene mõõtesari lennukil (T 2, l ) annab ainult ühe punkti. Valemi (10) kontrollimiseks antud nurga allφ 0 selliseid partiisid tuleb toota mitu.

Tehakse ettepanek teha iga nurga jaoks viis sellist mõõtesarja.φ 0 , mille jaoks on valitud järgmised kolm nurka:~ 0 \u003d umbes 10; ~ 0 \u003d umbes 20; φ 0 \u003d 30 lk.

Mitu mõõdetud väärtustl ja T. valitud nurga jaoksφ 0 nende aritmeetilised keskmised arvutatakse valemitega:

, (14)

kus n - mõõtmiste arv.

Mõõtmiste tulemusena peab õpilane täitma järgmised kolm tabelit eksperimentaalsete andmetega ja näitama neid õpetajale.

Tabel 1.

φ 0 \u003d 10 о
mõõtenumber	seeria 1		seeria 2		3. sari		seeria 4		5. jagu

Tabel 2.

φ 0 \u003d 20 о
mõõtenumber	seeria 1		seeria 2		3. sari		seeria 4		5. jagu

Tabel 3.

φ 0 \u003d 30 о
mõõtenumber	seeria 1		seeria 2		3. sari		seeria 4		5. jagu

Pikkuse mõõtmisell pendlit tuleb meeles pidada, et viimane koosneb palli hoidva keerme pikkusest ja palli raadiusest.

Palli raadius arvutatakse selle läbimõõdu kaudu, mida mõõdetakse vernieri nihikuga. Kuna pall ei esinda täiuslikku sfäärilist pinda, annab iga läbimõõdu mõõtmine väärtus, mis erineb veidi varem mõõdetud väärtusest.

Seadmel, mis rakendab pendli võnkumisi, on seade, mis reguleerib keerme pikkust. Sel juhul saab keerme pikkust mõõta kahel viisil: kas kinnitada kindla pikkusega niidile võrdlusniit, mille pikkus tuleb seejärel mõõta joonlauaga; või võtke teatava pikkusega niit võrdlusniidina ja kinnitage selle seadme reguleeritava seadme abil pendli niidi pikkus.

Liikuv platvorm (vt joonis 1) võimaldab teil pendli pikkust mõõta muul viisil. Selleks on vaja ühendada pendli niit palliga liikuva platvormi ülemise tasapinnaga (vt joonis 3). Platvormi sama positsiooni saab kinnitada mõõtjoonlauale - see on keerme pikkus koos palliga, millest tuleb lahutada palli raadius. Palli läbimõõt tuleb mõõta vernieri nihikuga.

Joonis: 3.

Periood T pendli võnkumised on kõige paremini määratletud järgmiselt: mõõta aegat mitu pendli võnkumist ja jagage see aeg siis võnkumiste arvuga. Tuleb meeles pidada, et ühe võnkumise aeg tähendab aega, mille jooksul pall naaseb ühest äärmuslikust asendist samasse asendisse.

Vajaliku nurga seadmiseksφ 0 on vaja kasutada ristkülikukujulist metallplaati, millel ühest punktist väljuvad mitu juhtjoont, mis on sellest punktist lähtuva vertikaalse joone suhtes eri nurkade all kaldu. Neid nurki saab mõõta kraadiga.

Liikuv platvorm võimaldab ristkülikukujulisel plaadil joonduda pendlikeerme riputuskohaga nii, et palli allasendis langeb plaadi vertikaalne joon kokku pendli keermega.

Pärast seda joondamist saab liikuva platvormi koos plaadiga kinnitada. Nüüd, kui niit on ühe või teise nurga alla suunatud, tuleb see joondada kindla nurga määrava plaadi ühe joonega (vt joonis 1)

IV ... Mõõtmistulemuste töötlemine

Ükskõik milline mõõdetud väärtusl ja T. Tabelites 1-3 esitatud andmed ei ole täpsed väärtused, kuna neid mõõdetakse teatud vigadega.

Sellistel juhtudel võetakse valemite (14) abil arvutatud aritmeetilised keskmised näidatud suuruste täpseteks väärtusteks. Seejärel tähendab mõõtmisviga kõigi mõõdetud väärtuste maksimaalse hälbe moodulit nende aritmeetilisest keskmisest. Nimelt viga ∆1 pendli pikkuse mõõtmised määratletakse järgmiselt

∆ 1 \u003d max | l i - l vrd |, (15)

ja viga ∆ 2 - pendli võnkeperiood tuleks arvutada järgmiselt:

∆ 2 \u003d max | T i - T av | ... (16)

Valemites (15) - (16) indeksi \u003d 1,2,3… jookseb läbi kõigi vastavate suuruste mõõtenumbrid.

Mõõtmistulemusi töötleme programmis arvutisMicrosoft Excel ning näidata konkreetsete mõõtmistulemuste jaoks vajalike arvutuste tehnoloogiat.

Olgu tabel 3 täidetud järgmiste tegelike andmetega.

Tabel 3

φ 0 \u003d 30 о
mõõtenumber	seeria 1		seeria 2		3. sari		seeria 4		5. jagu
	0,505 0,495 0,503 0,498 0,500	1,434 1,434 1,428 1,422 1,418	0,606 0,594 0,603 0,597 0,600	1,547 1,553 1,557 1,575 1,553	0,704 0,696 0,702 0,698 0,700	1,685 1,681 1,678 1,691 1,687	0,806 0,794 0,804 0,797 0,800	1,807 1,815 1,791 1,791 1,800	0,904 0,896 0,903 0,898 0,900	1,907 1,909 1,925 1,906 1,897

Iga mõõteseeria jaoks on vaja arvutada valemite abil (14)l av ja T av ja seejärel luua sõltuvusT cf 2 \u003d f (l cf) ... Mugavuse huvides tutvustame märget:T cf 2 \u003d y 1, l cf \u003d x 1.

Enne näidatud arvutustega jätkamist koostame programmisExcel tabel 3 ja valmistage ette tabeli 4 formaat, mille andmeid kasutatakse funktsionaalse sõltuvuse konstrueerimisely 1 \u003d f (x 1).

Excelis Tabel 3 moodustatakse järgmiselt.

Töövihiku 1. lehelExcel rakkude vahemiku aktiveerimineA 1: A 2, ühendage need ja sisestage klaviatuurilt saadud ühendatud lahtrisse esimese veeru pealkiri:n mõõtenumber", Aktiveerige lahtrivahemikB 1: C 1, ühendage need ja sisestage teise ja kolmanda veeru ühine päis klaviatuurilt saadud ühendatud lahtrisse:seeria 1 ", Aktiveerige lahterB 2 ja sisestage klaviatuurilt tabeli 3 teise veeru alapealkiri:l "Pärast seda aktiveerime lahtri C2 ja sisestame selle klaviatuurilt tabeli 3 kolmanda veeru alapealkirja:"T ". Kordame tabeli 3 ülejäänud veergude jaoks näidatud toiminguid. Ülaltoodud toimingute tulemusena saame tabeli 3 vormingu.

Nüüd täidame saadud vormingu tabeli 3 andmetega, mille tulemusena saame programmis tabeli 3Excel.

Tabelis 4 vormingu loomiseks programmisExcel töövihiku lehel1Excel lahtri aktiveerimineA 9 ja sisestage klaviatuurilt esimese veeru päis:n B 9 ja sisestage klaviatuurilt sinna teine \u200b\u200bveeru päis:l cf \u003d x 1 ". Samamoodi sisestame klaviatuurilt kolmanda, neljanda ja viienda veeru päised:T cf "," T cf 2 \u003d y 1 "ja" y 1 / x 1 "rakkudes C 1, D 1 ja E 1. Järgmisena aktiveerime lahtriA 10 ja sisestage klaviatuurilt lahtrisse number 1A 11 numbrit 2, aktiveerige lahtrivahemikA 10: A 11 ja täitke lahtrisse automaatseltA 14. Ülaltoodud toimingute sooritamise tulemusena saame tabeli 4.

Tabel 4.

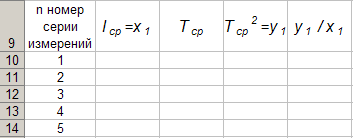
Näitame tabeli 4 esimese rea täitmise tehnoloogiat 1. seeria mõõtmiste töötlemisega.

Mille jaoks programmeerime esimese valemi punktis (14), saamel Kolmapäev ja pane see tabelisse 4.B 10 ja sisestage klaviatuurilt valem "\u003d SUM (B3: B7) * (1/5)".

Seejärel programmeerime (14) teise valemi.E 2 ja sisestage klaviatuurilt valem "\u003d SUM (C3: C7) * (1/5)".

Saame T av ja ruudutage see ning arvutage seejärel suhe. Selleks aktiveerige lahterD 10 ja sisestage klaviatuurilt valem "\u003d C10 ^ 2", seejärel aktiveerige lahterE 10 ja sisestage klaviatuurilt valem "\u003d D10 / B10". Pärast kõiki neid toiminguid on tabeli 4 esimene rida vormis

Pärast nende arvutuste korramist teiste seeriate jaoks võtab tabel 4 lõpliku kuju

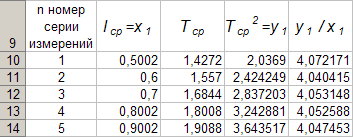
Tabeli 4 andmed võimaldavad programmi kasutadaExcel koostada funktsionaalse sõltuvuse graafiky 1 \u003d f (x 1).

Selleks aktiveerige lahtrivahemikD 10: D 14, helistame programmi funktsioonide viisardileExcel , valige diagrammi tüüp "Scatter", esimene vaade. Liigutage hiirekursor nupule "Järgmine" ja tehke hiire vasakut nuppu (LMB) üks klõps. Pärast seda minge vahekaardile Rida. Selleks liigutage hiire kursorit vahekaardil "Rida", mis asub akna "Diagrammiviisard" ülemises osas, ja tehke üks LMB klõps. Järgmisena asetage kursor väljale "X väärtused" ja seejärel liigutage hiirekursor lahtrisseB 10, vajutage LMB ja seda vabastamata liigutage hiirekursor lahtrisseB 14 ja seejärel vabastage LMB. Selle tulemusel valem “\u003d Sheet1! $B $ 10: B $ 14 dollarit. Nüüd liigutage hiirekursor nuppu "Järgmine" ja tehke kaks LMB klikki järjest, seejärel liigutage hiirekursor nuppu "Lõpeta" ja tehke üks LMB klõps. Töövihiku 1. lehelExcel ilmub funktsionaalse sõltuvuse graafiky 1 \u003d f (x 1) ... Aktiveerime rida 10 ja lisame uue rea, mille järel sisestame klaviatuurilt lahtritesseA 10: E 10-kohaline "0". Järgmisena viige hiirekursor diagrammi suvalisse punkti ja tehke üks LMB klõps. Suurendame diagrammi andmevahemikku, mille jaoks liigutame hiirekursori väärtuste vahemiku piiriley 1 ja liigutage piiri paremas ülanurgas asuv marker lahtrisseD 10. Teeme sama vahemikugax 1.

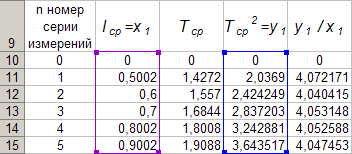
Nüüd liigutage hiirekursor graafiku suvalisse punkti ja tehke üks hiire parema nupuga klõps (RMB). Kuvatavas kontekstimenüüs liigutage hiirekursor käsule "Trendirea lisamine" ja tehke üks LMB klõps. Joonis 4 illustreerib nende konstruktsioonide tulemust.

Joonis 4.

Joonis 4 näitab, et sõltuvusy 1 \u003d f (x 1) on lineaarne ja seda kirjeldatakse võrrandiga

y 1 \u003d 4,04 8 x 1 + 0,00 24 (17)

Võrrand 17 näitab, et kallek võrrandist (10) võrdub:k \u003d 4,0493. Kui see väärtusk valemis (12) asendatud, siis saame raskuskiirenduse väärtuse.

Kallek võrrandis (10) saab tabeli 4 andmete põhjal arvutada valemiga

(18)

Selleks aktiveerige lahterA 17 ja sisestage valem „\u003d SUM (E 11: E 15) * (1/5) "

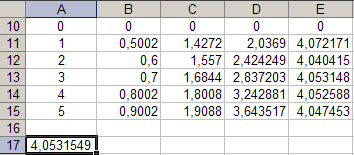
saame k \u003d 4,053, s.o number numbrile lähedalk saadud joonisel 4 toodud graafikult.

On ilmne, et valemiga (12) saadud arv, kasutades kogustk võrrandist (17) on mõni viga.

Selle vea arvutamiseks pöördume tagasi tabelites 3 ja 4 toodud andmete juurde.

Programmis esimeneExcel loome uue tabelivormingu 5. Miks töövihiku lehel1Excel lahtri aktiveerimineA 19 ja sisestage klaviatuurilt esimese veeru päis:n mõõteseeria number ", aktiveerige lahterB 19 ja sisestage klaviatuurilt sinna teine \u200b\u200bveeru pealkiri: “∆1 vastavalt punktile (15) ". Samamoodi sisestage klaviatuurilt kolmanda veeru päised: “∆2 kuni (16) "lahtrisse C 19. Seejärel aktiveerige lahterA 20 ja sisestage lahtrisse klaviatuurilt number 1A 21 numbrit 2, aktiveerige lahtrivahemikA 20: A 21 ja täitke lahtrisse automaatseltA 26. Ülaltoodud toimingute sooritamise tulemusena saame tabeli 5.

Tabel 5.

Valemite (15) ja (16) programmeerimisel on see vajalikl i ja T i , võtke iga mõõteseeria tabelist 3 jal av ja T av tabeli 4 andmetest.

∆ arvutamiseks1 esimese mõõteseeria jaoks on vaja rakk aktiveeridaM 3 ja sisestage klaviatuurilt valem "\u003d ABS (B3-B $ 11))", siis täidame automaatselt lahtrisseM 7. Nüüd lahtrisseB 20 sisestame klaviatuurilt valemi "\u003d MAX (M3: M7)".

∆ arvutamiseks2 sama seeria andmete kohaselt on vaja rakk aktiveeridaN 3 ja sisestage klaviatuurilt valem "\u003d ABS (C3-C $ 11)", mille järel täidame automaatselt lahtrisseN 7. Nüüd lahtrisseC 20 sisestame klaviatuurilt valemi "\u003d MAX (N3: N7)".

Selle tulemusena on tabel 5 vormis

Pärast muude mõõteseeriate andmete arvutamist vastavalt punktidele (15) ja (16) on tabel 5 vormis

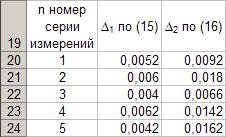
Tabeli 5 andmete põhjal on ilmne, et iga mõõteseeria puhul on täpsed pikkuse väärtusedl pendel ja perioodT pendli võnkumised on määratletud järgmiselt

l \u003d l av ± ∆ 1, T \u003d T av ± ∆ 2 (19)

Pealegi selgub, et ∆1 ja ∆ 2 on pendli iga pikkuse jaoks erinevad. Valemitest (19) järeldub, et joonisel 4 kujutatud sirgjoon tõmmatakse veaga ja selle läheduses on eksperimentaalsete andmete hajumine.

Katseandmete hajuvuse arvestamiseks arvutame veel kaks funktsionaalset sõltuvust:

(T av + ∆ 2) 2 \u003d f (l av + ∆ 1), (20)

(T av - ∆ 2) 2 \u003d f (l av - ∆ 1). (21)

Sõltuvuse (20) arvutamiseks tutvustame uusi nimetusi:

x 2 \u003d (l cf + ∆ 1), (22)

y 2 \u003d (T avg + ∆ 2) 2, (23)

Enne valemite (22) ja (23) abil arvutuste jätkamist moodustame programmi abil uue tabeli 6 vorminguExcel , vastavalt eelnevalt näidatud algoritmile, Siis saame

Tabel 6.

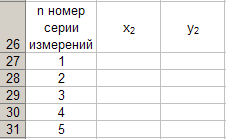
X 2 ja y 2 arvutamisel vastavalt punktidele (22) ja (23) on vaja kasutada tabelite 4 ja 5 andmeid. Esiteks arvutamex 2 ja saadud arvud kantakse tabelisse 6.

Selleks aktiveerige lahterB 27 ja sisestage klaviatuurilt valem "\u003d B11 + B20".

Seejärel arvutage y 2 selleks aktiveerime lahtriC 27 ja sisestage klaviatuurilt valem "\u003d (C11 + C20) ^ 2".

B 27: C 27 ja lahtrisse automaatne täitmineC 31.

Seejärel täidetakse tabel 6 järgmiste andmetega

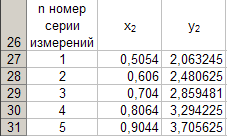
Vastavalt tabelile 6 koostame sõltuvuse graafikuy 2 \u003d y 2 (x 2) (vt joonis 5) vastavalt eelnevalt kirjeldatud tehnoloogiale

Joonis 5 näitab, et sõltuvusy 2 \u003d y 2 (x 2) on määratud võrrandiga

y 2 \u003d 4,08 86 x 2 - 0,002 3 (24)

Jätkame funktsionaalse sõltuvuse arvutamist (21). Selleks tutvustame kahte abivalemit

x 3 \u003d l cf - ∆ 1, (25)

y 3 \u003d (T av - ∆ 2) 2. (26)

Nende valemite järgi arvutatakse vastavalt tabelite 4 ja 5 andmetele ning nende arvutuste tulemused sisestatakse tabelisse 7. Kõigepealt arvutamex 3 ... Selleks aktiveerige lahterB 34 ja sisestage klaviatuurilt valem "\u003d B11-B20".

Seejärel arvutage y 3 selleks aktiveerime lahtriC 34 ja sisestage klaviatuurilt valem "\u003d (C11-C20) ^ 2".

Nüüd aktiveerime lahtrivahemikuB 34: C 34 ja täitke lahtrisse automaatseltC 38.

Selle tabeli andmed on järgmised

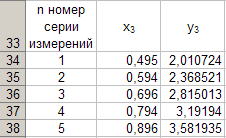
Funktsionaalne sõltuvusy 3 = y3 (x3 ) , mis on ehitatud vastavalt tabelile 7, on näidatud joonisel 6.

Joonis 6 viitab sellele

y3 = 4,00 7 3 x3 + 0,00 71 (27)

Kalde väärtusedk võrrandite (17), (24), (27) andmete järgi sisestame tabeli 8.

Programmeerime valemi (12) ja arvutamegigale väärtusele vastavk... Sisestame saadud väärtusedg tabelis 8. Selleks aktiveerige lahterC41 ja sisestage klaviatuurilt valem "\u003d (4 * PI () ^ 2) / B41". Pärast seda täidame lahtrisse automaatseltC43.

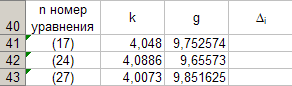
Nüüd arvutame keskmiseg valemi järgi

Selleks aktiveerige lahterC45 ja sisestage klaviatuurilt valem "\u003d (1/3) * SUM (C41: C43)".

See osutub võrdseks 9,75331-ga, mida võtame täpse väärtusena. Viga selle väärtuse määramiselg arvutatakse valemiga

Δ 3 = max | gi – gkolmapäev| = max | Δ i| (28)

Selleks aktiveerige lahterD41 ja sisestage klaviatuurilt valem "\u003d ABS (C41-C $ 45)". Pärast seda täidame lahtrisse automaatseltD43.

Me arvutameΔ i ja pane see tabelisse 8. Selleks aktiveerige lahterD45 ja sisestage klaviatuurilt valem "\u003d MAX (D41: D43)".

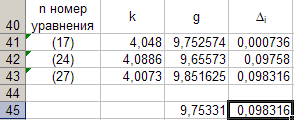
Tabeli 8 andmetest järeldub, etΔ 3 \u003d 0,098316. Nii et kiirendusg selle seadmega kaudsete mõõtmiste tulemusel saadud vabalangemine osutus

g \u003d 9,7533 ± 0,0983.

testi küsimused

1. Millised on matemaatilise pendli võnkumiste uurimise seadme elemendid.
2. Millise mehaanikaseaduse alusel koostatakse pendli liikumisvõrrand.
3. Millised on piirangud, mille alusel saadakse matemaatilise pendli liikumist simuleeriv võrrand.
4. Milliseid vibratsioone nimetatakse harmoonilisteks.
5. Andke määratlus võnkumiste amplituudile, faasile ja sagedusele.