I. Definition, basic properties and graphs of hyperbolic functions. Hyperbolic functions Th math function
11 Basic functions of a complex variable
Let us recall the definition of the complex exponent -. Then
Maclaurin series expansion. The radius of convergence of this series is + ∞, which means that the complex exponent is analytic on the whole complex plane and
(exp z) "= exp z; exp 0 = 1. (2)
The first equality here follows, for example, from the term-by-term differentiation theorem for a power series.
11.1 Trigonometric and hyperbolic functions
Sine complex variable called the function

Cosine of a complex variable there is a function

Hyperbolic sine of a complex variable defined like this:
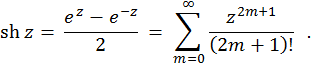
Hyperbolic cosine of a complex variable is a function

Let us note some properties of the newly introduced functions.
A. If x∈ ℝ, then cos x, sin x, ch x, sh x∈ ℝ.
B. There is the following connection between trigonometric and hyperbolic functions:
cos iz = ch z; sin iz = ish z, ch iz = cos z; sh iz = isin z.
B. Basic trigonometric and hyperbolic identities:
cos 2 z + sin 2 z = 1; ch 2 z-sh 2 z = 1.
Proof of the main hyperbolic identity.
The main trigonometric identity follows from the main hyperbolic identity when taking into account the connection between trigonometric and hyperbolic functions (see property B)
G Addition formulas:
In particular,
D. To calculate the derivatives of trigonometric and hyperbolic functions, one should apply the theorem on term-by-term differentiation of a power series. We get:
(cos z) "= - sin z; (sin z)" = cos z; (ch z) "= sh z; (sh z)" = ch z.
E. The functions cos z, ch z are even, and the functions sin z, sh z are odd.
G. (Periodicity) The function e z is periodic with a period of 2π i. The functions cos z, sin z are periodic with a period of 2π, and the functions ch z, sh z are periodic with a period of 2πi. Moreover,
Applying the sum formulas, we obtain
Z. Decompositions into real and imaginary parts:
If a single-valued analytic function f (z) maps bijectively a domain D onto a domain G, then D is called a domain of schlichtness.
AND. Domain D k = (x + iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
Proof. It follows from relation (5) that the mapping exp: D k → ℂ is injective. Let w be any nonzero complex number. Then, solving the equations e x = | w | and e iy = w / | w | with real variables x and y (choose y from a half-interval)