Изучение колебаний нитяного маятника и измерение. Лабораторная работа по физике "изучение законов математического маятника"
Изучение законов математического маятника
Цель работы: Изучить законы математического маятника и определить ускорение свободного падения
Оборудование: Маятник (шарик на подвесе), линейка, секундомер или часы с секундной стрелкой.
Краткая теория:
Математический маятник - осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения.
Длиной маятника l называется расстояние от точки подвеса до центра тяжести шарика.
Для практического расчета периода колебаний пользуются формулой:
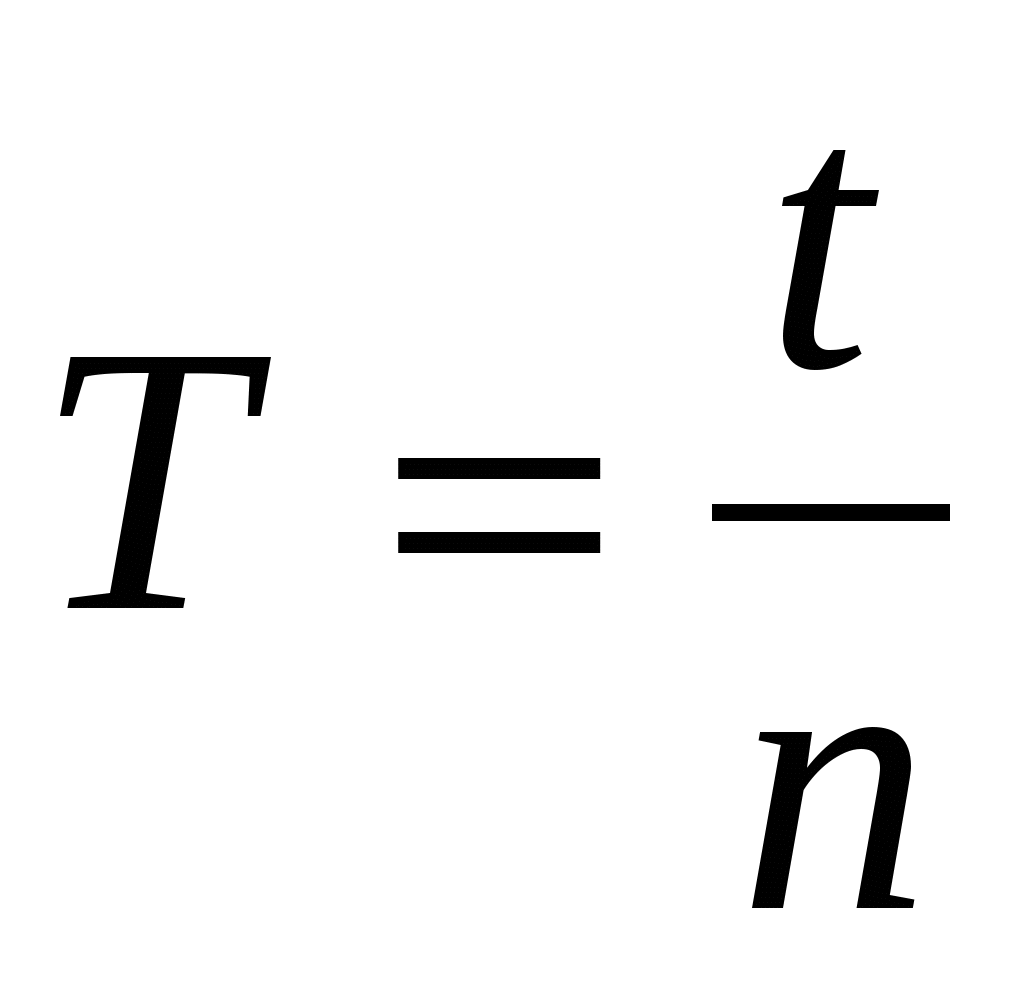 ,
,
где Т-период колебаний,
t – время колебаний,
n – число полных колебаний.
Согласно законам колебаний период маятника можно определить по формуле:
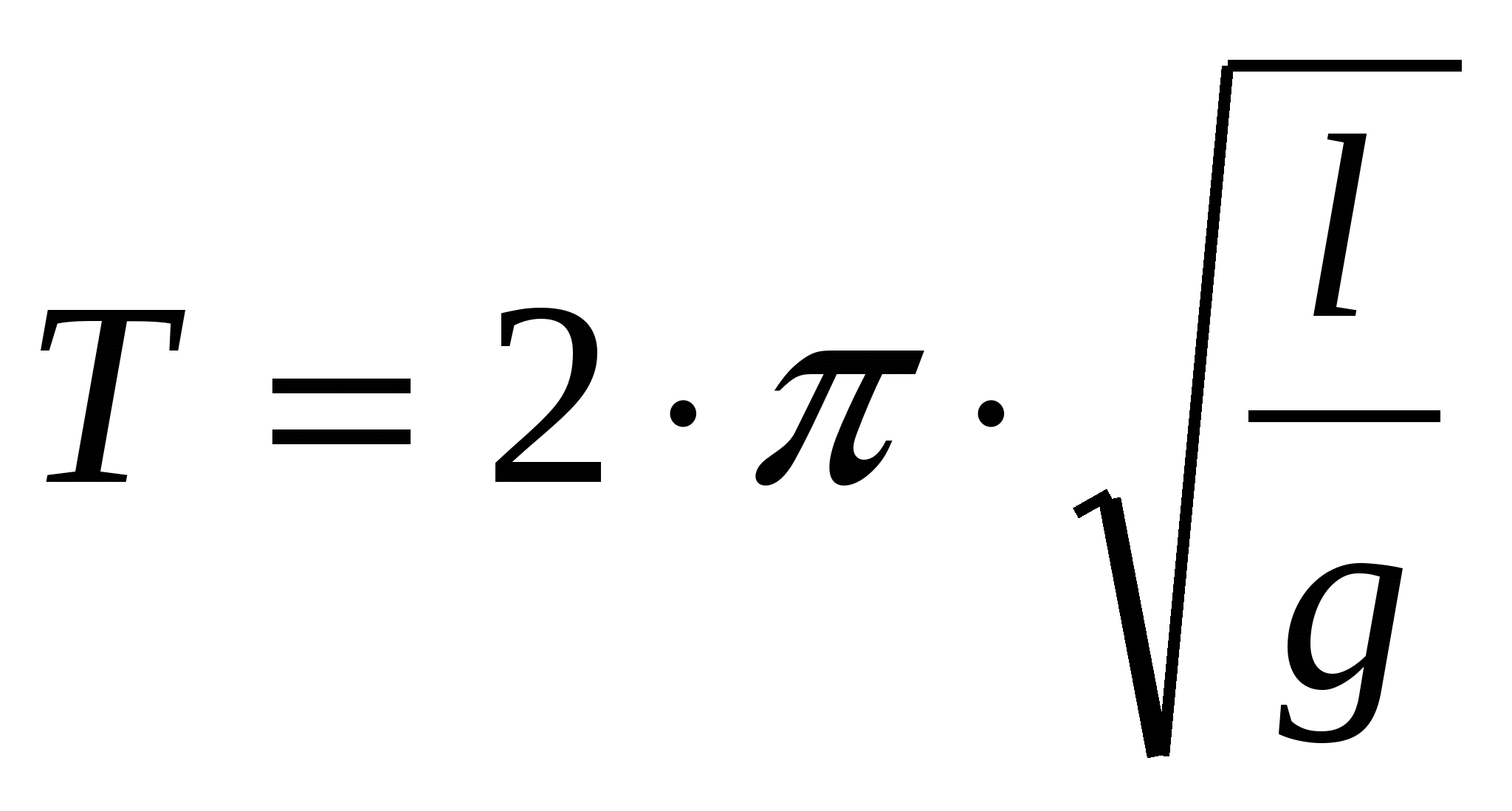 ,
,
Период колебаний математического маятника не зависит от массы шарика.
П ериод колебания математического маятника прямо пропорционален длине маятника и обратно пропорционален ускорению свободного падения. Данное уравнение называется формулой Гюйгенса.
ериод колебания математического маятника прямо пропорционален длине маятника и обратно пропорционален ускорению свободного падения. Данное уравнение называется формулой Гюйгенса.
Историческая справка
Христиан Гюйгенс ван Зёйлихем (14 апреля 1629- 8 июля 1695,). голландский физик, математик, механик и астроном и изобретатель. Родился в Гааге. Обучался в Лейденском университете юридическим наукам, но не прекращал занятия математикой. Опираясь на исследования Галилея, он решил ряд задач механики. В 1656 году в возрасте 27 лет им были сконструированы первые маятниковые часы со спусковым механизмом. Создание часов, измеряющих время с невиданной для той поры точностью, имело далеко идущие последствия для развития физического эксперимента и практической деятельности человека. До этого ведь время измеряли по истечению воды, горению факела или свечи. Созданная Гюйгенсом к 1673 году теория колебаний явилась одним из оснований для понимания потом природы света.
Из формулы Гюйгенса путем математических преобразований получаем выражение для ускорения свободного падения:
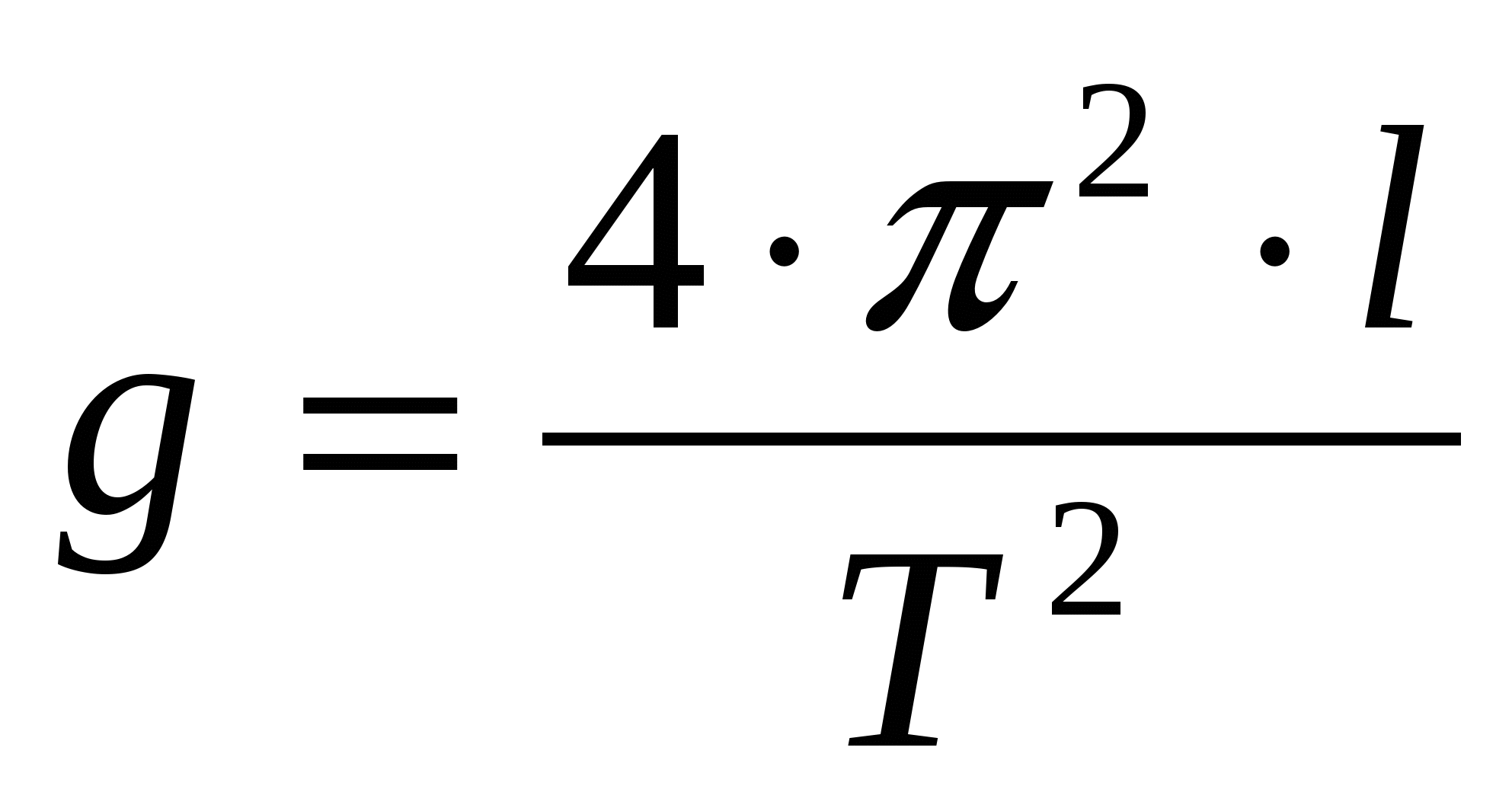

Реальной моделью математического маятника в наших опытах будет служить небольшой шарик, подвешенный на тонкой упругой нити. Размеры шарика должны быть малы по сравнению с длиной нити. Это дает возможность считать, что вся масса сосредоточена в одной точке, в центре тяжести шарика.
Ход работы:
Определить цену деления приборов:
линейка ……..м/дел.
секундомер…….с/дел.
2. Определить погрешность приборов (абсолютная погрешность приборов равна ½ цены деления):
линейка Δ l = ……..м
секундомер Δ t =…….с
Установить максимальную длину маятника и измерить ее l 1 =….м.
Запустить маятник (угол отклонения 10-15 0) и за время t подсчитать число колебаний n (не менее 7).
Изменяя число колебаний повторить опыт еще 3 раза.
t 2 =……… , n 2 =…………. T 2 =……… ,
t 3 =……… , n 3 =…………. T 3 =……… ,
t 4 =……… , n 4 =…………. T 4 =……… ,
Изменить длину маятника l 2 =….м и повторить все измерения.
Данные занести в таблицу.
№ измерения
Длина маятника,
l , м
№ опыта
Время колебаний,
t, с
Число колебаний,
n
Период колебаний,
Т, с
Среднее значение периода, Т ср, с
Ускорение свободного падения, g, м/с 2 .
Среднее значение
ускорения свободного падения, g ср, м/с 2 .
l ср=
t ср =
относительная: абсолютная:
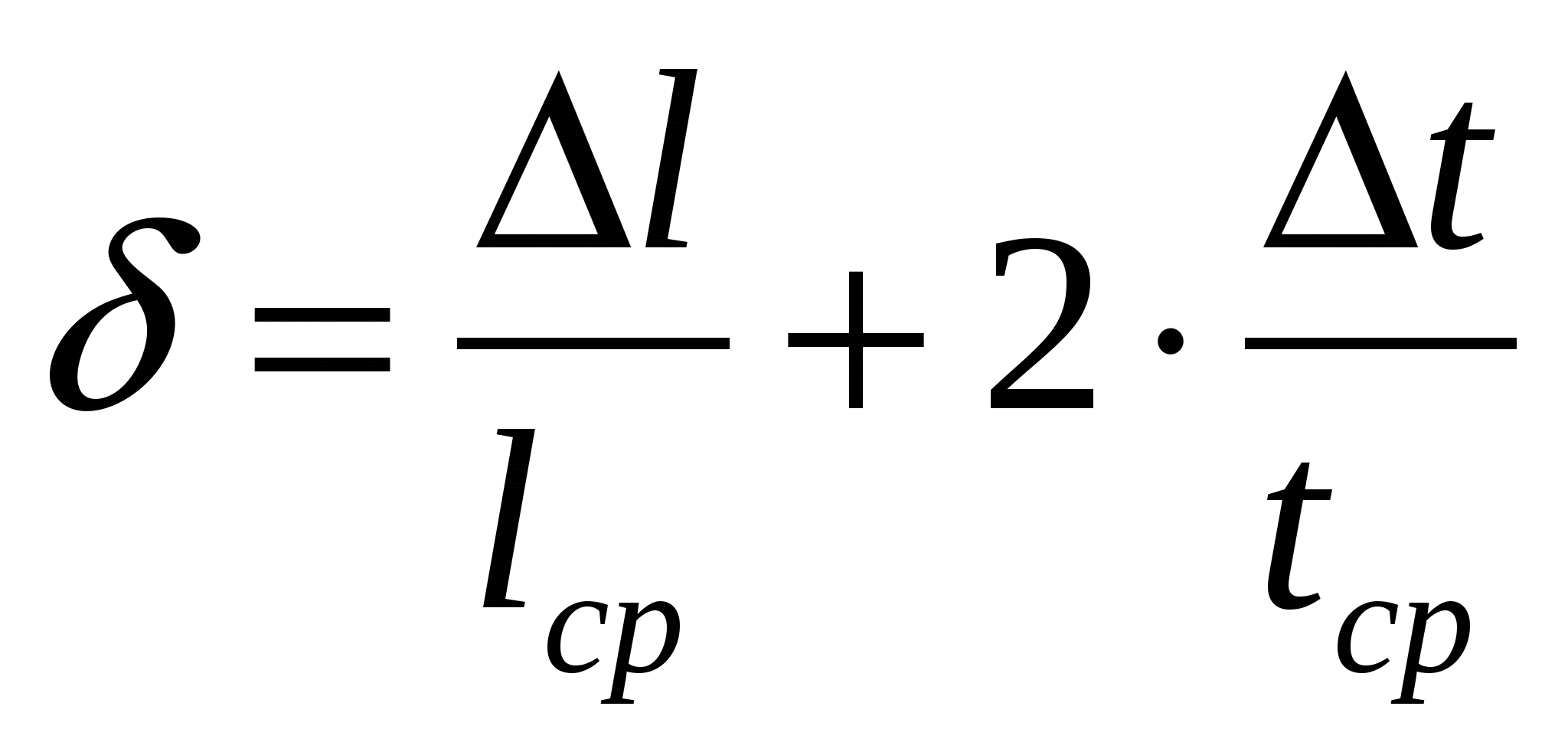
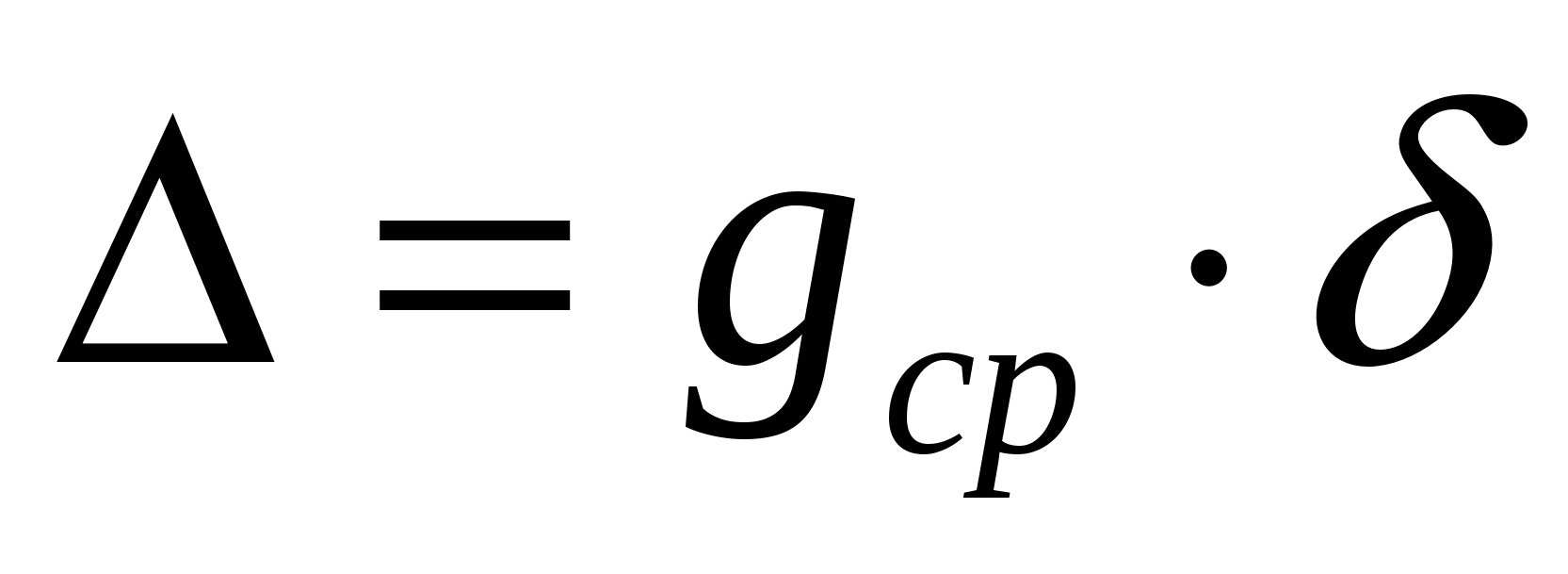 ,
,
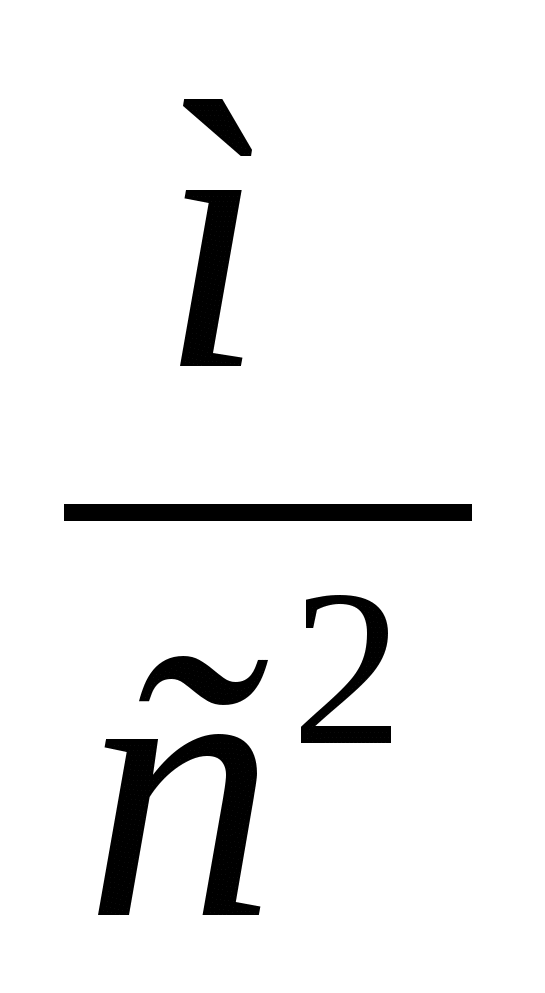
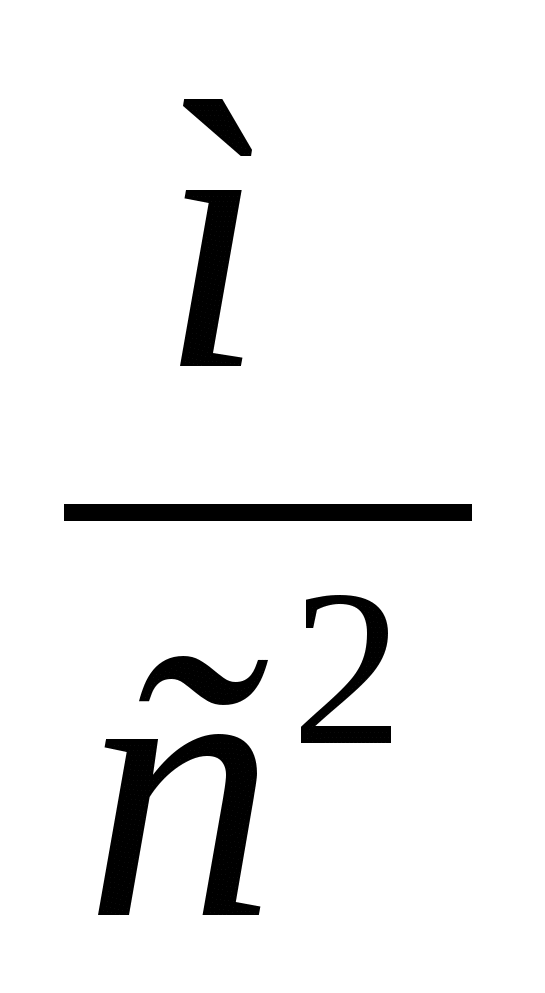
Контрольные вопросы:
Какую длину имеет математический маятник с периодом 2 с?
Найдите массу груза, который на пружине жесткостью 250 Н/м делает 20 колебаний за 16 с.
Ускорение свободного падения на Луне равно 1,7 м/с 2 .Каким будет период колебаний математического мятника на Луне, если на Земле он равен 1 с? Зависит ли ответ от массы груза?
Координата колеблющегося тела изменяется по закону х=0,5sin 45πt.Чему равна амплитуда и период колебаний?
Амплитуда незатухающих колебаний точки 12 см, линейная частота 14 Гц, начальная фаза колебаний равна 0. Написать уравнение движения точки х=х(t).
Цена деления шкалы
Разность (без учёта знака) между значениями физической величины, соответствующими отметкам шкалы, ограничивающими деление. В цифровых приборах характеристикой, заменяющей цену деления шкалы, служит шаг дискретности.
а) выбрать на шкале два ближайших оцифрованных штриха;
в) разность значений (из большего вычесть меньшее) около выбранных штрихов разделить на количество делений.
Н а этом рисунке в крупном масштабе показана шкала термометра. Проиллюстрируем с ее помощью правило для вычисления цены деления.
а этом рисунке в крупном масштабе показана шкала термометра. Проиллюстрируем с ее помощью правило для вычисления цены деления.
а) выбираем оцифрованные штрихи 20 °С и 40 °С
б) между ними 10 делений (промежутков)
в) вычисляем: (40 °С – 20 °С) : 10 делений = 2 °С/дел.
Ответ: цена делений = 2 °С/дел,
У цифровых приборов шкалы в явном виде нет, и на них вместо цены деления указывается цена единицы младшего разряда числа в показании прибора.
П
ример:
1) цена деления шкалы данного прибора составляет 1(условных ед.)/дел.
2
) цена деления шкалы данного прибора составляет 0,01(условных ед.)/дел.
3
) цена деления шкалы данного прибора составляет 0,1(условных ед.)/дел.
4) цена деления шкалы данного прибора составляет 0,001(условных ед.)/дел.

I . Цель работы
Наблюдения над колебательными движениями математического маятника, реализуемые на приборе, функциональная схема которого, представлена на рисунке 1.
Измерение периода колебаний маятника при различных длинах и амплитудах.
Определение режима изохронности колебаний математического маятника.
Вычисление ускорения свободного падения шарика по результатам указанных измерений.
II . Теоретическая часть
Рассмотрим прибор, состоящий из шарика небольших размеров, прикреплённого к неподвижной точке подвеса с помощью невесомой нерастяжимой нити определённой длины (рис. 1).
Если размеры шарика много меньше длины l нити, то шарик можно рассматривать как материальную точку; а если масса шарика много больше массы нити, то последнюю можно считать невесомой. Нить также можно считать нерастяжимой при условии, что сила тяжести шарика вызывает бесконечно малое удлинение нити.
Данный прибор позволяет моделировать колебательные движения так называемого математического маятника.
Рис. 1. Прибор для изучения колебаний математического маятника: 1. Металлическая пластина для установления угла отклонения маятника; 2. Подвижная платформа; 3. Измерительная линейка.

Рис 2. Иллюстрация колебательных движений математического маятника.
Действительно, в исходном состояние нить направлена вертикально вниз (положение 1 на рисунке 2). В этом случае сила F натяжения нити и сила mg тяжести шарика совпадают с направлением нити, но противоположно направлены. Так как нить нерастяжима, то обе силы уравновешивают друг друга, т.е. F = mg . Шарик находится в покое. Такое состояние маятника называется положением его равновесия.
Выведем маятник из положения равновесия, отклонив шарик от первоначального состояния на угол φ 0 (рис. 2). После чего отпустим его без толчка. Под действием силы тяжести mg шарик начнёт движение в сторону положения равновесия, через некоторое время перейдёт его, затем с другой стороны от положения равновесия отклонится от него на некоторый угол меньший чем φ 0 и под действием силы тяжести снова устремится в сторону положения равновесия. При отсутствии внешних воздействий на шарик последний будет совершать описанное движение в одной плоскости. Очевидно, что траекторией движения шарика будет дуга окружности радиуса l . Такие движения называются колебаниями.
Вследствие действия силы сопротивления на шарик, его колебания будут затухающими свидетельством чего служит то, что после каждого прохождения равновесия он будет отклоняться от него на всё меньший и меньший угол. Однако если наблюдать данный процесс в течение довольно короткого времени, то колебательный процесс можно признать незатухающим.
Рассмотрим силы, которые действуют на шарик в произвольный момент времени t . Пусть φ угол отклонения нити в этот момент. Запишем следующее уравнение второго закона Ньютона на направление τ , совпадающим с касательной, проведённой к той точке траектории движения шарика, в которой он находится в рассматриваемый момент времени t .
ma τ = - mg sin φ (1)
Здесь a τ тангенциальное ускорение, m масса шарика. Знак минус справа в (1) учитывает то обстоятельство, что при движении от положения равновесия вверх сила тяжести препятствует этому движению.
Угловое ускорение ε шарика определяется как вторая производная по времени от угла φ , т.е.
. (2)
Между тангенциальным ускорением a τ и угловым ε имеет место очевидная связь
(3)
Уравнение (1) с учётом формул (2) и (3) принимает вид:
. (4)
В уравнение (4) неизвестная функция φ(t ) стоит под знаком производной второго порядка. Такое уравнение в математике называют обыкновенным дифференциальным уравнением второго порядка.
Его можно упростить, если учесть, что при малых углах φ, измеренных в радианах. Тогда вместо (4) будем иметь
. (5)
Уравнение (5) описывает движение маятника. Его ещё называют уравнением гармонического осциллятора.
Непосредственной подстановкой можно убедиться в том, что решение уравнения (5) имеет вид
, (6)
если через обозначить
. (7)
Таким образом, видно, что изменения угла φ по времени происходит по синусоидальному закону. Величина φ 0 , равная максимальному углу отклонения от положения равновесия, называется амплитудой гармонических колебаний. Величина амплитуды в данном случае зависит от первоначального отклонения. Величина же стоящая под знаком синуса называется фазой. Фаза растёт пропорционально времени. Величина под знаком синуса называется начальной фазой, которая в рассматриваемом движении равна нулю.
Функция синуса, определяющая характер колебательных движений, суть периодическая функция с величиной периода равного. Последнее означает, что если через T обозначить период колебаний маятника, то можно написать следующее равенство для величины фазы
, (8)
где круговая частота.
Теперь с учётом (7) для периода Т будем иметь:
(9)
Соотношение (9) свидетельствует о том, что линеаризация уравнения (4) привела к уравнению (5), решение которого допускает независимость Т от амплитуды φ 0.
Такие колебания называются изохронными.
Формулу (9) можно ещё представить так:
k l , (10)
где через
(11)
обозначен угловой коэффициент линейной функциональной зависимости функции T 2 от аргумента l .
Следовательно, изохронность колебаний маятника проверяется справедливостью соотношения (10) по измеренным значениям периода T при различных значениях l , соотнесённых к одному и тому же углу φ 0 .
Функциональная зависимость, построенная по экспериментальным точкам, позволяет определить угловой коэффициент k , через числовое значение которого ускорение g свободного падения шарика вычисляется так:
. (12)
Кроме того по единичным измерениям T и l ускорение g можно вычислить ещё из такого соотношения:
(13)
III . Порядок проведения эксперимента
Так как линеаризация уравнения (4), приведшая к уравнению (5), описывающего изохронные колебания, основана на предположении, очевидно, что диапазон изохронности определяется значениями угла φ 0 при которых имеет место линейная зависимость.
Следовательно, чтобы определить диапазон значений φ 0 , при которых справедливо соотношение (10), необходимо для нескольких значений φ 0 произвести измерения, позволяющие построить зависимости, далее из указанных функциональных зависимостей вычислить угловой коэффициент k и для выбранных углов φ 0 вычислить значения g по (12), и сравнить их с общепринятым значением g = 9,8 м/с 2 . Те углы φ 0 , для которых вычисленная величина g с учётом погрешности измерений сохранит одинаковые числовые значения и определяет диапазон изохронности колебаний, реализуемых данным прибором.
Порядок измерений таков: выбирается конкретное значение угла φ 0 , на которое необходимо отклонить шарик от положения равновесия, устанавливается длина маятника, производится опыт, в процессе которого измеряется период T . Опыт производится несколько раз так, что при фиксированном угле φ 0 необходимо иметь от трёх до пяти измеренных значений l и T .
Это будет первая серия измерений, которая на плоскости (T 2 , l ) даст только одну точку. Для проверки формулы (10) при данном угле φ 0 необходимо произвести несколько таких серий.
Предлагается сделать по пять таких серий измерений для каждого из углов φ 0 , в качестве которых выбираются следующие три угла: φ 0 = 10 о ; φ 0 = 20 о ; φ 0 = 30 о .
По многократно измеренным значениям l и T для выбранного угла φ 0 вычисляются их средние арифметические по формулам:
, (14)
где n число измерений.
В результате проделанных измерений студент должен заполнить следующие три таблицы опытными данными и показать их преподавателю.
Таблица 1.
|
φ 0 = 10 о |
||||||||||
|
номер измерения |
серия 1 |
серия 2 |
серия 3 |
серия 4 |
серия 5 |
|||||
Таблица 2.
|
φ 0 = 20 о |
||||||||||
|
номер измерения |
серия 1 |
серия 2 |
серия 3 |
серия 4 |
серия 5 |
|||||
Таблица 3.
|
φ 0 = 30 о |
||||||||||
|
номер измерения |
серия 1 |
серия 2 |
серия 3 |
серия 4 |
серия 5 |
|||||
При проведении измерений длины l маятника необходимо иметь ввиду, что последняя слагается из длины нити, удерживающей шарик, и радиуса шарика.
Радиус шарика вычисляется через его диаметр, который измеряется штангенциркулем. Так как шарик не представляет идеальную сферическую поверхность, то каждое измерение диаметра будет давать величину, незначительно отличающуюся от ранее измеренной.
На приборе, реализующем колебательные движения маятника, имеется устройство, регулирующее длину нити. В таком случае длину нити можно измерять двояким образом: либо к нити фиксированной длины приложить эталонную нить, длину которой затем необходимо измерить на мерной линейке; либо в качестве эталонной нити взять нить определённой длины и по ней с помощью регулируемого устройства данного прибора зафиксировать длину нити маятника.
Подвижная платформа (см. рис. 1) позволяет измерять длину маятника ещё одним способом. Для этого необходимо нить маятника вместе с шариком совместить с верхней плоскостью подвижной платформы (см. рис. 3) Данное же положение платформы можно зафиксировать на измерительной линейке это будет длина нити вместе с шариком, из которой необходимо вычесть радиус шарика. Диаметр шарика необходимо измерить штангенциркулем.

Рис. 3.
Период T колебаний маятника лучше определять так: измерить время t нескольких колебаний маятника и затем разделить это время на число колебаний. При этом надо иметь ввиду, что под временем одного колебания подразумевается то время, в течение которого шарик из одного из крайних положений возвращается в то же положение.
Для установления требуемого угла φ 0 необходимо воспользоваться прямоугольной металлической пластиной, на которой из одной точки выходят несколько направляющих линий, наклонённых под различными углами к вертикальной линии, исходящей из этой точки. Эти углы можно измерить с помощью транспортира.
Подвижная платформа позволяет прямоугольную пластину совместить с точкой подвеса нити маятника так, чтобы вертикальная линия на пластине совпадала с нитью маятника, когда шарик находится в нижнем положении.
После указанного совмещения подвижную платформу вместе с пластиной можно закрепить. Теперь при отклонении нити на тот или иной угол её надо совместить с одной из линий пластины, определяющей конкретный угол (см. рис. 1)
IV . Обработка результатов измерений
Любое из измеренных значений l и T , представленных в таблицах 1-3 не являются точными величинами, так как они измерены с определёнными погрешностями.
В таких случаях в качестве точных значений указанных величин принимаются их средние арифметические, вычисляемые по формулам (14). Тогда под погрешностью измерения будем подразумевать модуль величины максимального отклонения всех измеренных величин от их среднего арифметического. А именно, погрешность ∆ 1 измерения длины маятника будем определять как
∆ 1 = max | l i - l ср |, (15)
а погрешность ∆ 2 - периода колебаний маятника следует вычислять так:
∆ 2 = max | T i T ср | . (16)
В формулах (15) - (16) индекс i = 1,2,3 … пробегает все номера измерений соответствующих величин.
Обработку результатов измерений будем производить на компьютере в программе Microsoft Excel и продемонстрируем технологию необходимых при этом расчётов на конкретных результатах измерений.
Пусть таблица 3 заполнена следующими фактическими данными.
Таблица 3
|
φ 0 = 30 о |
||||||||||
|
номер измерения |
серия 1 |
серия 2 |
серия 3 |
серия 4 |
серия 5 |
|||||
|
0,505 0,495 0,503 0,498 0,500 |
1,434 1,434 1,428 1,422 1,418 |
0,606 0,594 0,603 0,597 0,600 |
1,547 1,553 1,557 1,575 1,553 |
0,704 0,696 0,702 0,698 0,700 |
1,685 1,681 1,678 1,691 1,687 |
0,806 0,794 0,804 0,797 0,800 |
1,807 1,815 1,791 1,791 1,800 |
0,904 0,896 0,903 0,898 0,900 |
1,907 1,909 1,925 1,906 1,897 |
|
Для каждой серии измерений необходимо по формулам (14) вычислить l ср и T ср , а затем построить зависимость T ср 2 = f (l ср ) . Для удобства введём обозначения: T ср 2 = y 1 , l ср = x 1 .
Прежде чем перейти к указанным вычислениям построим в программе Excel таблицу 3 и заготовим формат таблицы 4, данные которой будут использованы при построении функциональной зависимости y 1 = f (x 1 ) .
В программе Excel таблица 3 формируется следующим образом.
На Листе1 рабочей книги Excel активизируем диапазон ячеек ячейку A 1: A 2, объединим их и занесём в получившуюся объединённую ячейку с клавиатуры заголовок первого столбца: « n номер измерения », активизируем диапазон ячеек B 1: C 1, объединим их и занесём в получившуюся объединённую ячейку с клавиатуры общий заголовок второго и третьего столбца: « серия 1 », активизируем ячейку B 2 и занесём в неё с клавиатуры подзаголовок второго столбца таблицы 3: « l » после чего, активизируем ячейку С2 и занесём в неё с клавиатуры подзаголовок третьего столбца таблицы 3: « T ». Повторим указанные действия для остальных столбцов таблицы 3. В результате выполнения вышеуказанных действий получим формат таблицы 3.
Теперь заполним полученный формат данными таблицы 3, в результате чего получим таблицу 3 в программе Excel .

Для построения формата таблицы 4 в программе Excel на Листе1 рабочей книги Excel активизируем ячейку A 9 и вводим в неё с клавиатуры заголовок первого столбца: « n B 9 и вводим в неё с клавиатуры заголовок второго столбца: « l ср = x 1 ». Аналогично заносим с клавиатуры заголовки третьего, четвёртого и пятого столбцов: « T ср », « T ср 2 = y 1 » и « y 1 / x 1 » в ячейки C 1, D 1 и E 1 соответственно. Далее, активизируем ячейку A 10 и занесём в неё с клавиатуры цифру 1, в ячейку A 11 цифру 2, активизируем диапазон ячеек A 10: A 11 и выполним автозаполнение до ячейки A 14. В результате выполнения вышеуказанных действий получим таблицу 4.
Таблица 4.
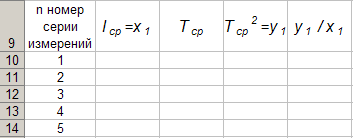
Технологию заполнения первой строки таблицы 4 продемонстрируем на обработке измерений серии 1.
Для чего программируем первую формулу в (14), получаем l ср и заносим в таблицу 4. B 10 и заносим с клавиатуры формулу «=СУММ(B3:B7)*(1/5)».
Потом программируем вторую формулу в (14). E 2 и заносим с клавиатуры формулу «=СУММ(C3:C7)*(1/5)».
Получаем T ср и возводим её в квадрат, после чего вычисляем отношение. Для этого активизируем ячейку D 10 и заносим с клавиатуры формулу «=C10^2», затем активизируем ячейку E 10 и заносим с клавиатуры формулу «=D10/B10». После всех этих действий первая строка таблицы 4 принимает вид

После повторения указанных расчётов для других серий Таблица 4 принимает окончательных вид
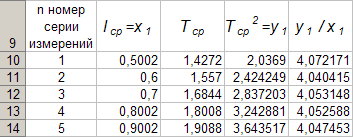
Данные таблицы 4 позволяют с помощью программы Excel построить график функциональной зависимости y 1 = f (x 1 ) .
Для этого активизируем диапазон ячеек D 10: D 14, вызовем Мастер Функций программы Excel , выберем тип диаграммы «Точечная», вид первый. Подведём курсор мыши к кнопке «Далее» и выполним однократное нажатие левой клавиши мыши (ЛКМ). После этого перейдём на вкладку Ряд. Для этого подведём курсор мыши в вкладке «Ряд», находящейся в верхней части окна «Мастер Диаграмм» и выполним однократное нажатие ЛКМ. Далее установим курсор в поле «Значения Х» после чего подведём курсор мыши к ячейке B 10, нажмём ЛКМ и не отпуская её переместим курсор мыши до ячейки B 14 после чего отпустим ЛКМ. В результате в поле «Значения Х» будет записана формула «=Лист1!$ B $10:$ B $14». Теперь подведём курсор мыши к кнопке «Далее» и выполним подряд два нажатия ЛКМ после чего переместим курсор мыши на кнопку «Готово» и выполним однократное нажатие ЛКМ. На Листе1 рабочей книги Excel появится график функциональной зависимости y 1 = f (x 1 ) . Активизируем строку 10 и добавим новую строку, после чего занесём с клавиатуры в ячейки A 10: E 10 цифру «0». Далее, Подведём курсор мыши к любой точке графика и выполним однократное нажатие ЛКМ. Увеличим диапазон данных графика, для чего подведём курсор мыши к границе диапазона значений y 1 и передвинем маркер, расположенный в правом верхнем углу границы до ячейки D 10. Аналогично поступим с диапазоном x 1 .
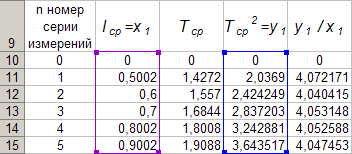
Теперь подведём курсор мыши к любой точке графика и выполним однократное нажатие правой клавиши мыши (ПКМ). В появившемся контекстном меню подведём курсор мыши к команде «Добавить линию тренда» и выполним однократное нажатие ЛКМ. Рисунок 4 иллюстрирует результат указанных построений.
Рис 4.
Из рисунка 4 следует, что зависимость y 1 = f (x 1 ) имеет линейный характер и описывается уравнением
y 1 = 4,04 8 x 1 + 0,00 24 (17)
Уравнение 17 показывает, что угловой коэффициент k из уравнения (10) оказывается равным: k = 4,0493. Если это значение k подставить в формулу (12), то получим величину ускорения свободного падения.
Угловой коэффициент k в уравнении (10) можно вычислить и из данных таблицы 4 по формуле
(18)
Для этого активизируем ячейку A 17 и занесём в неё с клавиатуры формулу «=СУММ(E 11: E 15)*(1/5)»
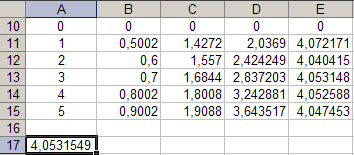
получим k = 4,053, т.е. число близкое к числу k , полученному из графика, изображённого на рисунке 4.
Очевидно, что число, полученное по формуле (12) с использованием величины k из уравнения (17) будет обладать некоторой погрешностью.
Чтобы вычислить эту погрешность вернёмся к данным таблиц 3 и 4.
Вначале в программе Excel создадим формат новой таблицы 5. Для чего на Листе1 рабочей книги Excel активизируем ячейку A 19 и занесём в неё с клавиатуры заголовок первого столбца: « n номер серии измерений», активизируем ячейку B 19 и занесём в неё с клавиатуры заголовок второго столбца: «∆ 1 по (15)». Аналогично занесём с клавиатуры заголовки третьего столбца: «∆ 2 по (16)» в ячейку C 19. Далее, активизируем ячейку A 20 и занесём в неё с клавиатуры цифру 1, в ячейку A 21 цифру 2, активизируем диапазон ячеек A 20: A 21 и выполним автозаполнение до ячейки A 26. В результате выполнения вышеуказанных действий получим таблицу 5.
Таблица 5.

При программировании формул (15) и (16) необходимо l i и T i , каждой серии измерений брать из таблицы 3, а l ср и T ср из данных таблицы 4.
Чтобы вычислить ∆ 1 для первой серии измерений необходимо активизировать ячейку M 3 и занести в неё с клавиатуры формулу «=ABS(B3-B$11))» после чего выполним автозаполнение до ячейки M 7. Теперь в ячейку B 20 занесём с клавиатуры формулу «=МАКС(M3:M7)».
Для вычисления ∆ 2 по данным той же серии необходимо активизировать ячейку N 3 и занести в неё с клавиатуры формулу «=ABS(C3-C$11)» после чего выполним автозаполнение до ячейки N 7. Теперь в ячейку C 20 занесём с клавиатуры формулу «=МАКС(N3:N7)».
В результате таблица 5 принимает вид

После выполнения расчётов по (15) и (16) для данных других серий измерений таблица 5 принимает вид
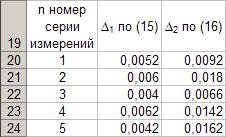
Из данных таблицы 5 очевидно, что для каждой серии измерений точные значения длины l маятника и периода T колебаний маятника определяются так
l = l ср ± ∆ 1 , T = T ср ± ∆ 2 (19)
При этом оказывается, что ∆ 1 и ∆ 2 различны для каждой из длин маятника. Из формул (19) следует, что прямая линия рисунка 4 проведена с погрешностью и в её окрестности имеет место так называемый разброс экспериментальных данных.
Чтобы учесть разброс опытных данных, вычислим ещё две функциональные зависимости:
(T ср + ∆ 2 ) 2 = f (l ср + ∆ 1 ) , (20)
(T ср - ∆ 2 ) 2 = f (l ср - ∆ 1 ) . (21)
Для вычисления зависимости (20) введём новые обозначения:
x 2 = (l ср + ∆ 1 ) , (22)
y 2 = (T ср + ∆ 2 ) 2 , (23)
Прежде чем приступить к вычислениям по формулам (22) и (23) образуем формат новой таблицы 6 с помощью программы Excel , по указанному ранее алгоритму, Тогда получим
Таблица 6.
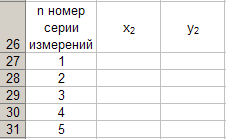
При вычислении x 2 и y 2 по (22) и (23) необходимо пользоваться данными таблиц 4 и 5. Вначале вычисляем x 2 и полученные числа заносим таблицу 6.
Для этого активизируем ячейку B 27 и занесём в неё с клавиатуры формулу «=B11+B20».
Затем вычисляем y 2 для этого активизируем ячейку C 27 и занесём в неё с клавиатуры формулу «=(C11+C20)^2».
B 27: C 27 и выполним автозаполнение до ячейки C 31.
После чего таблица 6 заполнится следующими данными
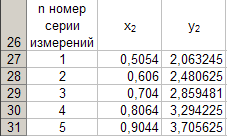
По данным таблицы 6 строим график зависимости y 2 = y 2 (x 2 ) (см. рис. 5) по описанной ранее технологии
Из рисунка 5 видно, что зависимость y 2 = y 2 (x 2 ) определяется уравнением
y 2 = 4,08 86 x 2 0,002 3 (24)
Переходим к вычислению функциональной зависимости (21). Для этого введём две вспомогательные формулы
x 3 = l ср - ∆ 1 , (25)
y 3 = (T ср - ∆ 2 ) 2 . (26)
Вычисление по этим формулам производится по данным таблиц 4 и 5, а результаты указанных вычислений заносятся в таблицу 7. Вначале вычисляем x 3 . Для этого активизируем ячейку B 34 и занесём в неё с клавиатуры формулу «=B11-B20».
Затем вычисляем y 3 для этого активизируем ячейку C 34 и занесём в неё с клавиатуры формулу «=(C11-C20)^2».
Теперь активизируем диапазон ячеек B 34: C 34 и выполним автозаполнение до ячейки C 38.
Данные этой таблицы оказываются следующими
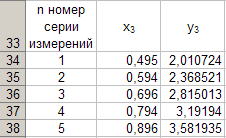
Функциональная зависимость y 3 = y 3 (x 3 ) , построенная по данным таблицы 7 указана на рисунке 6.
Из рисунка 6 следует, что
y 3 = 4,00 7 3 x 3 + 0,00 71 (27)
Значения углового коэффициента k по данным уравнений (17), (24), (27) заносим в таблицу 8.

Программируем формулу (12) и вычисляем g , соответствующее каждому значению k . Заносим полученные значения g в таблицу 8. Для этого активизируем ячейку C 41 и занесём в неё с клавиатуры формулу «=(4*ПИ()^2)/B41». После этого выполним автозаполнения до ячейки C 43.
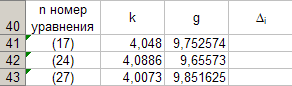
Теперь вычисляем среднее значение g по формуле
Для этого активизируем ячейку C 45 и занесём в неё с клавиатуры формулу «=(1/3)*СУММ(C41:C43)».

Оно оказывается равным 9,75331, которое принимаем за точное значением. Погрешность определения данного значения g вычисляем по формуле
Δ 3 = max | g i g ср | = max | Δ i | (28)
Для этого активизируем ячейку D 41 и занесём в неё с клавиатуры формулу «=ABS(C41-C$45)». После этого выполним автозаполнения до ячейки D43 .

Вычисляем Δ i и заносим в таблицу 8. Для этого активизируем ячейку D 45 и занесём в неё с клавиатуры формулу «=МАКС(D41:D43)».
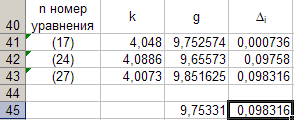
Из данных таблицы 8 следует, что Δ 3 = 0,098316. Таким образом, ускорение g свободного падения, полученное на данном приборе, в результате косвенных измерений оказалось равным
g = 9,7533 ± 0,0983.
Контрольные вопросы
- Из каких элементов состоит прибор для изучения колебаний математического маятника.
- На базе какого закона механики составляется уравнение движения маятника.
- При каких ограничениях получается уравнение, моделирующее движение математического маятника.
- Какие колебания называются гармоническими.
- Дайте определение амплитуды, фазы и частоты колебаний.