Def . Пусть ,
,

.

Множество называется замкнутым промежутком или замкнутым брусом в.

Множество называется открытым промежутком

или открытым брусом в .

Def . Мерой промежуткови называется величина:

(Точнее
).

Def . Если
такое, что
то промежутокназывается вырожденным и
.

Свойства меры промежутка:

а). Положительность:
, причем
тогда и только тогда, когда – вырожден.

б). Положительная однородность: .

в). Аддитивность:

* для
таких, что
;

* для
и

.

г). Монотонность меры: .

Def . Диаметром бруса (промежутка) называется величина:

Отметим, что
и
– это не одно и тоже. Например, если – вырожден, то
,a
(вообще говоря).

При этом: * ;

* ;*
.

Def . Совокупность
подпромежутков промежутканазывается разбиением промежутка, если: *;

*
; *
; *
; *
.

Величина
называется параметром разбиенияP (при этом
).

Def . Разбиениеназывается измельчением разбиения, если все элементы разбиенияполучены разбиением элементов разбиения.

Обозначается:
. Читается:мельчеиликрупнее.

Для отношения “ крупнее – мельче” справедливо:

*. транзитивность – ; *.
;

*.


; *.

|
.

§. Определение кратного интеграла

Пусть
– брус (промежуток) в,
– разбиение промежуткаI . На каждом из промежутков разбиенияотметим точку
.

Получим
разбиение с отмеченными точками для
.

Величина
называется интегральной суммой Римана для функцииf (x ) на промежуткеI по разбиению с отмеченными точками
.

Def :
=
=
.

Обозначая – множество функций интегрируемых на брусеI запишем:

Def : ε > 0δ>0<.

Если для функции f (x ) наI и разбиения
– обозначить через
– наибольшее и наименьшее значение функцииf (x ) наI k то величины
=
и
=
называются нижней и верхней суммами Дарбу.

§. Критерий Дарбу существования кратного интеграла .

Т 0 . Чтобы функция
была интегрируема на брусе(т.е.
) необходимо и достаточно, чтобы

. Δ▲.

Определено интегрирование функции по брусу в евклидовом пространстве. А как функцию проинтегрировать по произвольному ограниченному множеству из евклидового пространства?

Определим интеграл от функции f по множеству
.

Def : Пусть
и
– ограничено, т.е.
. Функцию
назовём характеристической функцией множестваM .

Тогда:
≡
.

Определение интеграла по множеству не зависит от того, какой брус, содержащий М выбран, т.е.

.

Это обозначает, что определение интеграла по множеству корректно.

Необходимое условие интегрируемости. Чтобы функцияf (x ) наМ была интегрируемой необходимо, чтобыf (x ) была ограниченной наМ . Δ▲.

§. Свойства кратных интегралов.

1  . Линейность: МножествоR M функций интегрируемых на множествеМ – линейное

пространство, а
– линейный функционал.

2  . Условие нормировки:
. Другая форма записи
по сути дела определяет меру произвольного множества из евклидового пространства.

3  . Если интеграл по множеству Лебеговой меры ноль существует, то он

равен нулю.

Примечание: МножествоМ называется множеством Лебеговой меры ноль,

если

такие, что
и
.

4  . а. ;б. ;

в. если
и– отделена от нуля наМ , то

5  .
иf =g п.в. (почти всюду) наМ , то
.

6  . Аддитивность: Если
и
то

,

В общем случае:
.

Δ. Следует из равенства: ▲

7  . Монотонность:
и
то
.

8  . Интегрирование неравенств: если
ито

.

9  . Пусть


. Для того чтобы
, необходимо и достаточно чтобы существовала внутренняя точка множестваМ , в которойf (x ) > 0 и непрерывна.

10  . Интегрируемость модуля интегрируемой функции:
.

11  . Теорема о среднем:
,
наМ сохраняет знак и
, то

.

Если множество М – связно иf (x ) – непрерывна на
то
такое, что
.

12  . Для того чтобы интеграл от неотрицательной функции был равен 0

необходимо и достаточно, чтобы f (x ) = 0 почти всюду наМ .

13  . Теорема Фубини. Для двойного интеграла:

Пусть область
– прямоугольник:. Тогда, при условии существования внутренних однократных интегралов, для нахождения двойного интеграла можно перейти к повторному интегрированию (см. рис. а):

, или

Е

сли область интегрирования не прямоугольник, теорема Фубини все равно справедлива и имеет вид (см. рис. б):
. (*)

Примечание: Внешние пределы интегрирования должны быть константами, внутренние пределы интегрирования могут зависеть от переменной, по которой интегрирование ещё предстоит.

Формула (*) может быть получена с использованием характеристической функции множества D .

Для многократного интеграла:

Пусть инекоторые подмножества евклидовых пространстви. Определим декартово произведение этих множеств, являющееся подмножеством евклидового пространства
:.

Тогда теорема Фубини для
имеет вид:
.

Теорема справедлива и для брусов X иY , и для более сложных конфигураций.

Примеры:

1 0 . Вычислить
, если граница области
задана уравнениями:

. Находя точки пересечения кривых определяющих границу области, получаем две точки:
и
. Тогда возможная расстановка пределов интегрирования при переходе к повторным интегралам дает:

а).
;

2

0 . Изменить порядок интегрирования в повторном интеграле:
.

–

.

Рецепт: При расстановке пределов интегрирования в двойном интеграле рекомендуется начинать с внешних пределов интегрирования.

3

0 . Вычислить:
, если

Переход к повторным интегралам даёт:
.

При этом, в тройном интеграле расстановку пределов надо начинать с внутренних пределов интегрирования. Затем спроецировать область V на плоскостьxOy

расставив пределы в области D – лежащей в плоскостиxOy .

4 0 . Изменить порядок интегрирования в повторном интеграле:
.

Остановимся несколько подробнее на работах Остроградского по кратным интегралам.

Формула Остроградского для преобразования тройного интеграла в двойной, которую мы пишем обычно в виде

где div A - дивергенция поля вектора А,

Аn - скалярное произведение вектора А на единичный вектор внешней нормали n граничной поверхности, в математической литературе нередко связывалась ранее с именами Гаусса и Грина.

На самом деле в работе Гаусса о притяжении сфероидов можно усмотреть только весьма частные случаи формулы (1), например при P=x, Q=R=0 и т. п. Что касается Дж. Грина, то в его труде по теории электричества и магнетизма формулы (1) вовсе нет; в нем выведено другое соотношение между тройным и двойным интегралами, именно, формула Грина для оператора Лапласа, которую можно записать в виде

Конечно, можно вывести формулу (1) и из (2), полагая

и точно так же можно получить формулу (2) из формулы (1), но Грин этого и не думал делать.

где слева стоит интеграл по объему, а справа интеграл по граничной поверхности, причем суть направляющие косинусы внешней нормали.

Парижские рукописи Остроградского свидетельствуют, с полной несомненностью, что ему принадлежит и открытие, и первое сообщение интегральной теоремы (1). Впервые она была высказана и доказана, точно так, как это делают теперь в “Доказательстве одной теоремы интегрального исчисления”, представленном Парижской Академии наук 13 февраля 1826 г., после чего еще раз была сформулирована в той части “Мемуара о распространении тепла внутри твердых тел ”, которую Остроградский представил 6 августа 1827 г. “Мемуар” был дан на отзыв Фурье и Пуассону, причем последний его, безусловно читал, как свидетельствует запись на первых страницах обеих частей рукописи. Разумеется, Пуассону и не приходила мысль приписывать себе теорему, с которой он познакомился в сочинении Остроградского за два года до представления своей работы на теории упругости.

Что касается взаимоотношения работ по кратным интегралам Остроградского и Грина, напомним, что в “Заметке по теории теплоты” выведена формула, обнимающая собственную формулу Грина, как весьма частный случай. Непривычная теперь символика Коши, употребленная Остроградским в “Заметке”, до недавнего времени скрывала от исследователей это важное открытие. Разумеется, за Грином остается честь открытия и первой публикации в 1828 г. носящей его имя формулы для операторов Лапласа.

Открытие формулы преобразования тройного интеграла в двойной помогло Остроградскому решить проблему варьирования п-кратного интеграла, именно, вывести понадобившуюся там общую формулу преобразования интеграла от выражения типа дивергенции по п- мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид

Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала.

В “Мемуаре об исчислении вариаций кратных интегралов” рассмотрены еще два важных вопроса теории таких интегралов. Во-первых, Остроградский выводит формулу замены переменных в многомерном интеграле; во-вторых, впервые дает полное и точное описание приема вычисления п- кратного интеграла с помощью п последовательных интеграций по каждой из переменных в соответствующих пределах. Наконец, из формул, содержащихся в этом мемуаре, легко выводится общее правило дифференцирования по параметру многомерного интеграла, когда от этого параметра зависит не только подынтегральная функция, но и граница области интегрирования. Названное правило вытекает из наличных в мемуаре формул настолько естественным образом, что позднейшие математики даже отождествляли его с одною из формул этого мемуара.

Замене переменных в кратных интегралах Остроградский посвятил специальную работу. Для двойного интеграла соответствующее правило вывел с помощью формальных преобразований Эйлер, для тройного - Лагранж. Однако, хотя результат Лагранжа верен, рассуждения его были не точными: он как бы исходил из того, что элементы объемов в старых и новых переменных - координатах - между собою равны. Аналогичную ошибку допустил вначале в только что упомянутом выводе правила замены переменных Остроградский. В статье “О преобразовании переменных в кратных интегралах” Остроградский раскрыл ошибку Лагранжа, а также впервые изложил тот наглядный геометрический метод преобразования переменных в двойном интеграле, который, в несколько более строгом оформлении, излагается и в наших руководствах. Именно, при замене переменных в интеграле по формулам, область интегрирования разбивается координатными линиями двух систем u=const, v=const на бесконечно малые криволинейные четырехугольники. Тогда интеграл можно получить, складывая сначала те его элементы, которые отвечают бесконечно узкой криволинейной полосе, а затем, продолжая суммировать элементы полосами, пока они все не будут исчерпаны. Несложный подсчет дает для площади, которая с точностью до малых высшего порядка может рассматриваться как параллелограмм, выражение, где, выбирается так, чтобы площадь была положительной. В итоге получается известная формула

Для функции двух переменных, заданной как z = f (x , y ) .

Записывается двойной интеграл так:

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.

Вычислить двойной интеграл - значит найти число, равное площади упомянутой фигуры D .

Пока мы не касаемся определения двойного интеграла , а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .

В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D - криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.

Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.

Случай прямоугольной области:

Случай криволинейной области:

А это уже решение знакомых нам определённых интегралов , в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.

Сведение двойного интеграла к повторному

Случай прямоугольной области

Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл , нужно свести его к повторному интегралу, который имеет вид

.

Сначала нужно вычислять внутренний (правый) определённый интеграл, затем - внешний (левый) определённый интеграл.

Можно и поменять ролями x и y

.

Пример 1. Вычислить двойной интеграл

Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.

.

Пример 2. Вычислить двойной интеграл

,

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

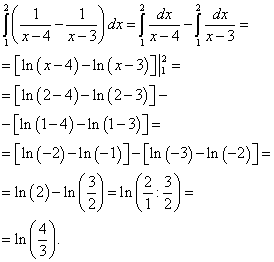
Результат и будет решением данного двойного интеграла.

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение

Случай криволинейной или треугольной области

Пусть снова дана функция двух переменных f (x , y ) , а ограничения для D : уже несколько другого вида:

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области - прямые x = a и x = b , но снизу и сверху - кривые, которые заданы уравнениями и . Иными словами, и - функции.

Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

.

Здесь пределы интегрирования a и b - числа, а и - функции. В случае треугольной области одна из функций или - это уравнение прямой линии. Такой случай будет разобран в примере 3.

Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем - левый определённый интеграл.

Точно так же можно поменять ролями x и y . Тогда повторный интеграл будет иметь вид

.

Такой повторный интеграл нужно решать точно так же: сначала - внутренний (правый) интеграл, затем - внешний (левый).

Пример 5. Вычислить двойной интеграл

,

Решение. Сводим данный двойной интеграл к повторному интегралу

.

На чертеже строим область интегрирования и видим, что она треугольная:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

.

Вычисляем первое слагаемое:

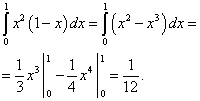
Вычисляем второе слагаемое:

Вычисляем третье слагаемое:

Получаем сумму, которая и будет решением данного двойного интеграла:

.

Пример 6. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

x -правильная и неправильная, y -правильная и неправильная области интегрирования

Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:

1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;

2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.

Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x , то область интегрирования называется x -неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x -правильной

Аналогично, если границу, заданную линиями, выраженными через y , прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y -неправильной. Вывести теперь признаки y -правильной области, надо полагать, совсем просто.

До сих пор мы рассматривали примеры с x -неправильными и y -правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.

Пример 7. Вычислить двойной интеграл , область интегрирования которого ограничена линиями y = x , xy = 1 , y = 2 .

Решение. Область интегрирования является y -неправильной, так как её нижнюю границу нельзя задать одной линией y = y (x ) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части - и .

Вычисляется этот двойной интеграл так:

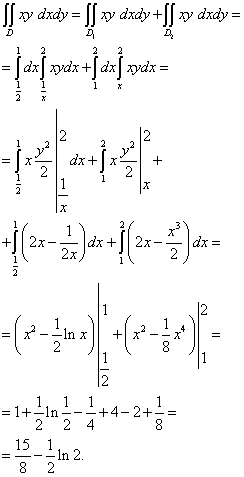
Смена порядка интегрирования

Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.

Смена порядка интегрирования образно может быть описана следующими словами О"Генри: "Так ведёт себя обитатель джунглей - зверь, попав в клетку, и так ведёт себя обитатель клетки - человек, заблудившись в джунглях сомнений". Результат, так же по О"Генри один и тот же: "Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд". (О"Генри . Шехерезада с Мэдисон-сквера .)

Тогда, если левый интеграл у нас по переменной x , а правый - по y , то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для "нового" игрека нужно "позаимствовать" у "старого" икса, а пределы интегрирования для "нового" икса получить в виде обратной функции , разрешив относительно икса уравнение, задававшее предел для игрека.

Пример 8.

.

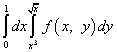Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу - правым. Пределы интегрирования для "нового" игрека позаимствуем у "старого" икса, то есть нижний предел равен нулю, а верхний - единице. Пределы интегрирования для "старого" игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:

(нижний) и (верхний).

Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

.

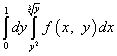После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y -неправильную или x -неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.

Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.

Пример 9. Сменить порядок интегрирования для повторного интеграла

.

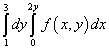Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .

При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x /2 , что видно на рисунке ниже.

Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:

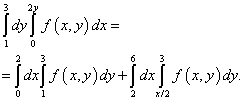
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.

Пример 10. Сменить порядок интегрирования для повторного интеграла

.

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми и .

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.

Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.

Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:

Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.

И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге - расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла - таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и - почти на автомате - на разбиении области и опустим само решение.

Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Решение. В явном виде (через x и y "без примесей") линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:

y ≤ 2x ;
y ≥ x /2;
y ≤ 2/x .

Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y -неправильной, так как её верхнюю границу нельзя задать одной линией y = y (x ) .

Скачать с Depositfiles

Лекции 5-6

Тема2. Кратные интегралы.

Двойной интеграл.

Контрольные вопросы.

1. Двойной интеграл, его геометрический и физический смысл

2. Свойства двойного интеграла.

3. Вычисление двойного интеграла в декартовых координатах.

4. Замена переменных в двойном интеграле. Вычисление двойного интеграла в полярных координатах.

Пусть функция z = f (x , y ) определена в ограниченной замкнутой области D плоскости. Разобьём область D произвольным образом на n элементарных замкнутых областей  1 , … , n , имеющих площади   1 , …,   n и диаметры d 1 , …, d n соответственно. Обозначим d наибольший из диаметров областей  1 , … ,  n . В каждой области  k выберем произвольную точку P k (x k ,y k ) и составим интегральную сумму функции f (x,y )

S =
(1)

Определение. Двойным интегралом функции f (x,y ) по области D называется предел интегральной суммы

, (2)

если он существует.

Замечание. Интегральная сумма S зависит от способа разбиения области D и выбора точек P k (k =1, …, n ). Однако, предел
, если он существует, не зависит от способа разбиения области D и выбора точек P k .

Достаточное условие существования двойного интеграла. Двойной интеграл (1) существует, если функция f (x,y ) непрерывна в D за исключением конечного числа кусочно-гладких кривых и ограничена в D . В дальнейшем будем считать, что все рассматриваемые двойные интегралы существуют.

Геометрический смысл двойного интеграла.

Если f (x,y ) ≥0 в области D , то двойной интеграл (1) равен объему «цилиндрического” тела, изображенного на рисунке:

V =
(3)

Цилиндрическое тело ограничено снизу областью D , сверху  частью поверхности z = f (x , y ), с боков  вертикальными отрезками прямых, соединяющих границы этой поверхности и области D.

Физический смысл двойного интеграла. Масса плоской пластины.

Пусть задана плоская пластина D с известной функцией плотности γ(х, у ), тогда разбивая пластину D на части D i и выбирая произвольные точки
, получим для массы пластины
, или, сравнивая с формулой (2):

(4)

4. Некоторые свойства двойного интеграла.

Линейность. Если С – числовая константа, то

Аддитивность. Если область D « разбита” на области D 1 и D 2 , то

3) Площадь ограниченной области D равна

(5)

Вычисление двойного интеграла в декартовых координатах.

Пусть задана область

Рисунок 1

D = { (x , y ): a ≤ x ≤ b , φ 1 (x ) ≤ y≤ φ 2 (x ) } (6)

Область D заключена в полосе между прямыми x = a , y = b , снизу и сверху ограничена соответственно кривыми y = φ 1 (x ) и y = φ 2 (x ) .

Двойной интеграл (1) по области D (4) вычисляется переходом к повторному интегралу:

(7)

Этот повторный интеграл вычисляется следующим образом. Сначала вычисляется внутреннийинтеграл

по переменной y , п ри этомx считаетсяпостоянной. В результате получится функция от переменной x , а затем вычисляется « внешний” интеграл от этой функции по переменной x .

Замечание. Процесс перехода к повторному интегралу по формуле (7) часто называют расстановкой пределов интегрирования в двойном интеграле. При расстановке пределов интегрирования нужно помнить два момента. Во-первых, нижний предел интегрирования не должен превышать верхнего, во-вторых, пределы внешнего интеграла должны быть константами, а внутреннего должны в общем случае зависеть от переменной интегрирования внешнего интеграла.

Пусть теперь область D имеет вид

D = { (x , y ) : c ≤ y ≤ d , ψ 1 (y ) ≤ x ≤ ψ 2 (y ) } . (8)

Тогда

. (9)

Предположим, что область D можно представить в виде (6) и (8) одновременно. Тогда имеет место равенство

(10)

Переход од одного повторного интеграла к другому в равенстве (10) называется изменением порядка интегрирования в двойном интеграле.

Примеры.

1) Изменить порядок интегрирования в интеграле

Решение. По виду повторного интеграла находим область

D = { (x , y ): 0 ≤ x ≤ 1, 2 x ≤ y≤ 2 } .

Изобразим область D . По рисунку видим, что эта область расположена в горизонтальной полосе между прямыми y =0, y =2 и между линиями x =0 и x = D

Иногда для упрощения вычислений делают замену переменных:

,
(11)

Если функции (11) непрерывно дифференцируемы и определитель (Якобиан) отличен от нуля в рассматриваемой области:

(12)

Министерство образования и науки Российской Федерации

Курсовая работа

По дисциплине: Высшая математика

(Основы линейного программирования)

На тему: КРАТНЫЕ ИНТЕГРАЛЫ

Выполнил: ______________

Преподаватель:___________

Дата ___________________

Оценка _________________

Подпись ________________

ВОРОНЕЖ 2008

1 Кратные интегралы

1.1 Двойной интеграл

1.2 Тройной интеграл

1.3 Кратные интегралы в криволинейных координатах

1.4 Геометрические и физические приложения кратных интегралов

2 Криволинейные и поверхностные интегралы

2.1 Криволинейные интегралы

2.2 Поверхностные интегралы

2.3 Геометрические и физические приложения

Список используемой литературы

1 Кратные интегралы

1.1 Двойной интеграл

Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией L. Разобьем эту область какими-нибудь линиями на п частей

, а соответствующие наибольшие расстояния между точками в каждой из этих частей обозначим d 1 , d 2 , ..., d n . Выберем в каждой части точку Р i .

Пусть в области D задана функция z = f(x, y). Обозначим через f(P 1), f(P 2),…, f(P n) значения этой функции в выбранных точках и составим сумму произведений вида f(P i)ΔS i:

, (1)

называемую интегральной суммой для функции f(x, y) в области D.

Если существует один и тот же предел интегральных сумм (1) при

и , не зависящий ни от способа разбиения области D на части, ни от выбора точек P i в них, то он называется двойным интегралом от функции f(x, y) по области D и обозначается . (2)

Вычисление двойного интеграла по области D, ограниченной линиями

x = a, x = b(a < b), где φ 1 (х) и φ 2 (х) непрерывны на (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла: = (3)

1.2 Тройной интеграл

Понятие тройного интеграла вводится по аналогии с двойным интегралом.

Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью S. Зададим в этой замкнутой области непрерывную функцию f(x, y, z). Затем разобьем область V на произвольные части Δv i , считая объем каждой части равным Δv i , и составим интегральную сумму вида

, (4)

Предел при

интегральных сумм (11), не зависящий от способа разбиения области V и выбора точек P i в каждой подобласти этой области, называется тройным интегралом от функции f(x, y, z) по области V: . (5)

Тройной интеграл от функции f(x,y,z) по области V равен трехкратному интегралу по той же области:

. (6)

1.3 Кратные интегралы в криволинейных координатах

Введем на плоскости криволинейные координаты, называемые полярными. Выберем точку О (полюс) и выходящий из нее луч (полярную ось).

Рис. 2 Рис. 3

Координатами точки М (рис. 2) будут длина отрезка МО – полярный радиус ρ и угол φ между МО и полярной осью: М(ρ,φ). Отметим, что для всех точек плоскости, кроме полюса, ρ > 0, а полярный угол φ будем считать положительным при измерении его в направлении против часовой стрелки и отрицательным – при измерении в противоположном направлении.

Связь между полярными и декартовыми координатами точки М можно задать, если совместить начало декартовой системы координат с полюсом, а положительную полуось Ох – с полярной осью (рис. 3). Тогда x=ρcosφ, у=ρsinφ . Отсюда

, tg.

Зададим в области D, ограниченной кривыми ρ=Φ 1 (φ) и ρ=Φ 2 (φ), где φ 1 < φ < φ 2 , непрерывную функцию z = f(φ, ρ) (рис. 4).

(7)

В трехмерном пространстве вводятся цилиндрические и сферические координаты.

Цилиндрические координаты точки Р(ρ,φ,z) – это полярные координаты ρ, φ проекции этой точки на плоскость Оху и аппликата данной точки z (рис.5).

Рис.5 Рис.6

Формулы перехода от цилиндрических координат к декартовым можно задать следующим образом:

x = ρcosφ, y = ρsinφ, z = z. (8)

В сферических координатах положение точки в пространстве определяется линейной координатой r – расстоянием от точки до начала декартовой системы координат (или полюса сферической системы), φ – полярным углом между положительной полуосью Ох и проекцией точки на плоскость Оху, и θ – углом между положительной полуосью оси Оz и отрезком OP (рис.6). При этом

Зададим формулы перехода от сферических координат к декартовым:

x = rsinθcosφ, y = rsinθsinφ, z = rcosθ. (9)

Тогда формулы перехода к цилиндрическим или сферическим координатам в тройном интеграле будут выглядеть так:

, (10)

где F 1 и F 2 – функции, полученные при подстановке в функцию fвместо x, y, z их выражений через цилиндрические (8) или сферические (9) координаты.

1.4 Геометрические и физические приложения кратных интегралов

1) Площадь плоской области S:

(11)

Пример 1.

Найти площадь фигуры D, ограниченной линиями

Эту площадь удобно вычислять, считая у внешней переменной. Тогда границы области задаются уравнениями

и
вычисляется с помощью интегрирования по частям: