บรรยายอินทิกรัลหลายตัว, อินทิกรัลคู่ การคำนวณอินทิกรัลคู่: ทฤษฎีและตัวอย่าง การแก้อินทิกรัลพหุคูณ

Def . ปล่อยให้เป็น
,

.

ชุดเรียกว่าช่องว่างปิดหรือแถบปิดใน .

ชุดเรียกว่า open gap

หรือแถบเปิดใน .

Def . การวัดช่วงเวลา และ ปริมาณเรียกว่า:

(อย่างแม่นยำมากขึ้น
).

Def . ถ้า
ดังนั้น
จากนั้นช่วงเวลา เรียกว่าเสื่อมและ
.

คุณสมบัติการวัดระยะห่าง:

NS). แง่บวก:
, และ
ถ้าและเฉพาะถ้า - มีความเสื่อมโทรม

NS). ความสม่ำเสมอในเชิงบวก:.

วี) สารเติมแต่ง:

* สำหรับ
ดังนั้น
;

* สำหรับ
และ

.

NS). ความน่าเบื่อของการวัด:.

Def . เส้นผ่านศูนย์กลางของแท่ง (ช่องว่าง) คือค่า:

สังเกตว่า
และ
ไม่ใช่สิ่งเดียวกัน ตัวอย่างเช่น if - เสื่อมแล้ว
, NS
(พูด, พูดแบบทั่วไป, พูดทั่วๆไป).

โดยที่: * ;

* ;*
.

Def . มวลรวม
ระยะห่างย่อย เรียกว่าการแบ่งช่วง , ถ้า: *;

*
; *
; *
; *
.

ปริมาณ
เรียกว่าพารามิเตอร์พาร์ติชั่น NS(ในที่นั้น
).

Def . แยก เรียกว่าการกลั่นพาร์ติชั่น ถ้าองค์ประกอบทั้งหมดของพาร์ทิชัน ได้มาจากการแยกองค์ประกอบที่แยกออก .

มันถูกระบุ:
... อ่าน: เล็กกว่า หรือ ใหญ่ขึ้น .

สำหรับความสัมพันธ์ที่ใหญ่กว่า-เล็กกว่านั้น มันเป็นความจริง:

*. ทรานซิชั่น -; *.
;

*.

; *.

|
.

§. ความหมายของอินทิกรัลพหุคูณ

ปล่อยให้เป็น
- ไม้ (ช่องว่าง) ใน ,
- แยกช่องว่าง ผม... ในแต่ละช่วงเวลาของพาร์ติชัน ทำเครื่องหมายจุด
.

เราได้รับ
แบ่งด้วยคะแนนที่ทำเครื่องหมายไว้สำหรับ
.

ปริมาณ
เรียกว่าอินทิกรัลผลรวมรีมันน์สำหรับฟังก์ชัน NS (NS) ในช่วงเวลา ผม โดยแบ่งด้วยคะแนนที่ทำเครื่องหมาย
.

Def :
=
=
.

แสดงถึง - ชุดของฟังก์ชันที่รวมเข้ากับบาร์ ผม เราเขียนลงไป:

Def : ε > 0 δ>0<.

ถ้าสำหรับฟังก์ชัน NS(NS) บน ผมและแยกออก
- แสดงโดย
- ค่าสูงสุดและต่ำสุดของฟังก์ชัน NS(NS) บน ผม kแล้วปริมาณ
=
และ
=
เรียกว่าผลรวม Darboux ล่างและบน

§. เกณฑ์ Darboux สำหรับการมีอยู่ของอินทิกรัลพหุคูณ.

NS 0 . ในการทำงาน
ถูกรวมเข้ากับบาร์ (เหล่านั้น.
) มีความจำเป็นและเพียงพอว่า

. Δ▲.

การรวมฟังก์ชันเหนือแท่งในสเปซแบบยุคลิดถูกกำหนด จะรวมฟังก์ชั่นเข้ากับชุดขอบเขตโดยพลการจากอวกาศแบบยุคลิดได้อย่างไร

ให้เรากำหนดอินทิกรัลของฟังก์ชัน NS โดยชุด
.

Def : ปล่อยให้เป็น
และ
- จำกัด เช่น
... การทำงาน
เรียกว่า ฟังก์ชันคุณลักษณะของเซต NS.

แล้ว:
≡
.

คำจำกัดความของอินทิกรัลเหนือเซตไม่ได้ขึ้นอยู่กับแท่งที่มี NSที่เลือกไว้ กล่าวคือ

.

ซึ่งหมายความว่าคำจำกัดความของอินทิกรัลเหนือเซตนั้นถูกต้อง

เงื่อนไขที่จำเป็นสำหรับการบูรณาการในการทำงาน NS(NS) บน NSสามารถบูรณาการได้จึงจำเป็นที่ NS(NS) จำกัดไว้ที่ NS. Δ▲.

§. คุณสมบัติของอินทิกรัลหลายตัว

1  . ความเป็นเส้นตรง: Many NS NSฟังก์ชันที่รวมเข้ากับชุด NS -เชิงเส้น

อวกาศและ
- ฟังก์ชันเชิงเส้น

2  . สภาวะปกติ:
... สัญกรณ์อีกรูปแบบหนึ่ง
อันที่จริงแล้วกำหนดการวัดของชุดโดยพลการจากอวกาศแบบยุคลิด

3  . หากอินทิกรัลเหนือชุดของ Lebesgue วัดศูนย์อยู่ แสดงว่า

เป็นศูนย์

บันทึก:มากมาย NSเรียกว่า ชุดเลเบสเกอวัดศูนย์

ถ้า

ดังนั้น
และ
.

4  . NS.;NS.;

วีถ้า
และ - แยกออกจากศูนย์โดย NS, แล้ว

5  .
และ NS=NSพีซี (เกือบทุกที่) บน NS, แล้ว
.

6  . สารเติมแต่ง: If
และ
แล้ว

โดยทั่วไป:
.

Δ ตามมาจากความเท่าเทียมกัน: ▲

7  . เสียงเดียว:
และ
แล้ว
.

8  . บูรณาการของอสมการ: if
อิโตะ

9  . ปล่อยให้เป็น

... ถึง
มีความจำเป็นและเพียงพอที่จะมีจุดภายในของเซต NS, โดยที่ NS (NS)> 0 และต่อเนื่อง

10  . ความสามารถในการบูรณาการของโมดูลของฟังก์ชันที่รวมเข้าด้วยกัน:
.

11  . ทฤษฎีบทเฉลี่ย:
,
บน NSรักษาเครื่องหมายและ
, แล้ว

ถ้าชุด NS- เชื่อมต่อและ NS(NS) ต่อเนื่องบน
แล้ว
ดังนั้น
.

12  . เพื่อให้อินทิกรัลของฟังก์ชันที่ไม่เป็นลบมีค่าเท่ากับ 0

จำเป็นและเพียงพอเพื่อ NS(NS) = 0 เกือบทุกที่บน NS.

13  . ทฤษฎีบทของฟูบินิสำหรับอินทิกรัลคู่:

ให้ภูมิภาค
- สี่เหลี่ยมผืนผ้า:. จากนั้น ภายใต้เงื่อนไขของการมีอยู่ของอินทิกรัลเดี่ยวภายใน เพื่อค้นหาอินทิกรัลคู่ เราสามารถดำเนินการรวมซ้ำได้ (ดูรูปที่ A):

, หรือ

อี

หากโดเมนของการบูรณาการไม่ใช่สี่เหลี่ยมผืนผ้า ทฤษฎีบทของ Fubini ยังคงใช้ได้และมีรูปแบบ (ดูรูปที่ b):

. (*)

บันทึก:ขีดจำกัดภายนอกของการรวมควรเป็นค่าคงที่ ขีดจำกัดภายในของการรวมอาจขึ้นอยู่กับตัวแปรที่ยังคงต้องทำการรวม

สามารถหาสูตร (*) ได้โดยใช้ฟังก์ชันคุณลักษณะของเซต NS.

สำหรับอินทิกรัลหลายตัว:

ให้บางส่วนของช่องว่างแบบยุคลิด และ ... เรากำหนดผลคูณคาร์ทีเซียนของเซตเหล่านี้ ซึ่งเป็นเซตย่อยของสเปซแบบยุคลิด
:.

แล้วทฤษฎีบทของ Fubini สำหรับ
ดูเหมือนกับ:
.

ทฤษฎีบทนี้ใช้ได้กับแท่งด้วย NSและ Yและสำหรับการกำหนดค่าที่ซับซ้อนยิ่งขึ้น

ตัวอย่าง:

1 0 . คำนวณ
ถ้าชายแดนของภูมิภาค
กำหนดโดยสมการ:

... การหาจุดตัดของเส้นโค้งที่กำหนดขอบเขตของพื้นที่ เราได้สองจุด:

และ

... จากนั้นการจัดเรียงที่เป็นไปได้ของขีดจำกัดของการรวมเมื่อส่งผ่านไปยังอินทิกรัลแบบวนซ้ำจะให้:

NS).
;

0 . เปลี่ยนลำดับของการรวมใน re-integral:

–

สูตรอาหาร:เมื่อตั้งค่าขีดจำกัดของการผสานรวมในอินทิกรัลคู่ ขอแนะนำให้เริ่มต้นด้วยขีดจำกัดภายนอกของการผสานรวม

0 . คำนวณ:

, ถ้า

การส่งผ่านไปยังอินทิกรัลที่วนซ้ำจะทำให้:
.

ในกรณีนี้ ในอินทิกรัลสามตัว การจัดเรียงขีดจำกัดต้องเริ่มต้นด้วยขีดจำกัดภายในของการผสานรวม แล้วฉายพื้นที่ วีบนเครื่องบิน xOy

กำหนดขอบเขตในพื้นที่ NS- นอนอยู่บนเครื่องบิน xOy.

4 0 . เปลี่ยนลำดับของการรวมใน re-integral:
.

ให้เราอาศัยรายละเอียดเพิ่มเติมอีกเล็กน้อยเกี่ยวกับงานของ Ostrogradskii เกี่ยวกับปริพันธ์หลายตัว

สูตรของ Ostrogradsky สำหรับการแปลงอินทิกรัลสามตัวเป็นอินทิกรัลคู่ซึ่งเรามักจะเขียนในรูปแบบ

โดยที่ div A คือความแตกต่างของสนามของเวกเตอร์ A

An คือผลคูณสเกลาร์ของเวกเตอร์ A โดยเวกเตอร์หน่วยของเส้นตั้งฉากภายนอก n ของพื้นผิวขอบเขต ในวรรณคดีคณิตศาสตร์ มันมักจะเกี่ยวข้องกับชื่อของเกาส์และกรีนก่อนหน้านี้

อันที่จริงในงานของเกาส์เรื่องแรงดึงดูดของทรงกลม เราสามารถมองเห็นได้เฉพาะกรณีพิเศษของสูตร (1) เช่น สำหรับ P = x, Q = R = 0 เป็นต้น สำหรับ J. Green ในงานของเขา เกี่ยวกับทฤษฎีไฟฟ้าและไม่มีสูตรแม่เหล็ก (1) เลย ได้มาซึ่งความสัมพันธ์ระหว่างปริพันธ์สามเท่าและปริพันธ์อีกประการหนึ่ง กล่าวคือ สูตรของกรีนสำหรับตัวดำเนินการลาปลาซ ซึ่งสามารถเขียนได้ในรูปแบบ

แน่นอน มันเป็นไปได้ที่จะได้รับสูตร (1) จาก (2) โดยการตั้งค่า

และในทำนองเดียวกัน คุณจะได้สูตร (2) จากสูตร (1) แต่กรีนไม่ได้คิดจะทำสิ่งนี้ด้วยซ้ำ

โดยที่อินทิกรัลเหนือปริมาตรอยู่ทางซ้าย และอินทิกรัลเหนือพื้นผิวขอบอยู่ทางด้านขวา และนี่คือทิศทางโคไซน์ของเส้นตั้งฉากด้านนอก

ต้นฉบับของชาวปารีสของ Ostrogradsky เป็นพยานด้วยความมั่นใจว่าทั้งการค้นพบและการสื่อสารครั้งแรกของทฤษฎีบทปริพันธ์ (1) เป็นของเขา เป็นครั้งแรกที่มีการแสดงและพิสูจน์เช่นเดียวกับที่ทำใน "การพิสูจน์ทฤษฎีบทของแคลคูลัสเชิงปริพันธ์" ที่นำเสนอต่อ Paris Academy of Sciences เมื่อวันที่ 13 กุมภาพันธ์ พ.ศ. 2369 หลังจากนั้นได้มีการกำหนดสูตรอีกครั้งในส่วนนั้น “บันทึกเรื่องการแพร่กระจายของความร้อนภายใน ของแข็ง” ซึ่ง Ostrogradsky นำเสนอเมื่อวันที่ 6 สิงหาคม 2370“ Memoir ” มอบให้ Fourier และ Poisson เพื่อตรวจสอบและคนหลังอ่านอย่างแน่นอนตามหลักฐานจากรายการในหน้าแรกของทั้งสองส่วนของต้นฉบับ แน่นอนว่าปัวซองไม่ได้คิดที่จะอธิบายทฤษฎีบทให้กับตัวเองซึ่งเขาพบในงานของ Ostrogradsky เมื่อสองปีก่อนการนำเสนอผลงานของเขาเกี่ยวกับทฤษฎีความยืดหยุ่น

สำหรับความสัมพันธ์ระหว่างงานของอินทิกรัลหลายตัวของ Ostrogradskii และ Green เราจำได้ว่าใน "หมายเหตุเกี่ยวกับทฤษฎีความร้อน" มีการสร้างสูตรที่รวมเอาสูตรของ Green ไว้เป็นกรณีพิเศษ สัญลักษณ์ที่ผิดปกติในขณะนี้ของ Cauchy ซึ่งใช้โดย Ostrogradsky ใน "Note" จนกระทั่งเมื่อไม่นานมานี้ได้ซ่อนการค้นพบที่สำคัญนี้จากนักวิจัย แน่นอน Greene ยังคงรักษาเกียรติของการค้นพบนี้และตีพิมพ์ครั้งแรกในปี 1828 ของสูตรสำหรับผู้ปฏิบัติงาน Laplace ที่มีชื่อของเขา

การค้นพบสูตรสำหรับการแปลงอินทิกรัลสามส่วนเป็นอินทิกรัลคู่ช่วย Ostrogradskii แก้ปัญหาการแปรผันของอินทิกรัล n-fold กล่าวคือเพื่อให้ได้สูตรทั่วไปสำหรับการแปลงอินทิกรัลของนิพจน์ของประเภทของไดเวอร์เจนซ์ เหนือโดเมน n- มิติและอินทิกรัลเหนือพื้นผิวซุปเปอร์พื้นผิวที่มีขอบเขต S ด้วยสมการ L (x, y, z, ...) = 0 หากเรายึดตามสัญกรณ์ก่อนหน้า สูตรจะมีรูปแบบ

อย่างไรก็ตาม Ostrogradsky ไม่ได้ใช้รูปภาพเรขาคณิตและคำศัพท์ที่เราใช้: ตอนนั้นยังไม่มีเรขาคณิตของช่องว่างหลายมิติ

ใน Memoir on the Calculus of Variations of Multiple Integrals มีการพิจารณาคำถามที่สำคัญอีกสองข้อเกี่ยวกับทฤษฎีของปริพันธ์ดังกล่าว อย่างแรก Ostrogradskii อนุมานสูตรสำหรับการเปลี่ยนแปลงของตัวแปรในอินทิกรัลหลายมิติ ประการที่สอง เป็นครั้งแรกที่เขาให้คำอธิบายที่สมบูรณ์และถูกต้องเกี่ยวกับวิธีการคำนวณอินทิกรัล n-fold โดยใช้การรวม n แบบต่อเนื่องกันในแต่ละตัวแปรภายในขอบเขตที่เหมาะสม สุดท้าย จากสูตรที่มีอยู่ในบันทึกนี้ อนุมานได้ง่าย กฎทั่วไปความแตกต่างที่สัมพันธ์กับพารามิเตอร์ของอินทิกรัลหลายมิติ เมื่อไม่เพียงแต่อินทิกรัลเท่านั้น แต่ยังรวมถึงขอบเขตของขอบเขตของการรวมเข้าด้วยกันด้วยขึ้นอยู่กับพารามิเตอร์นี้ กฎนี้สืบเนื่องมาจากสูตรที่มีอยู่ในไดอารี่ในลักษณะที่เป็นธรรมชาติที่นักคณิตศาสตร์ในภายหลังถึงกับระบุสูตรนี้ด้วยสูตรหนึ่งของไดอารี่นี้

Ostrogradskii อุทิศงานพิเศษให้กับการเปลี่ยนแปลงของตัวแปรในปริพันธ์หลายตัว สำหรับอินทิกรัลคู่ กฎที่สอดคล้องกันได้มาจากการแปลงแบบเป็นทางการโดยออยเลอร์ สำหรับอินทิกรัลสามตัวโดยลากรองจ์ อย่างไรก็ตาม แม้ว่าผลลัพธ์ของ Lagrange จะถูกต้อง แต่การให้เหตุผลของเขาไม่ถูกต้อง: ดูเหมือนว่าเขาจะดำเนินการต่อจากข้อเท็จจริงที่ว่าองค์ประกอบระดับเสียงในตัวแปรเก่าและใหม่ - พิกัด - มีค่าเท่ากัน Ostrogradskii ทำผิดพลาดในลักษณะเดียวกันในการกล่าวถึงกฎสำหรับการเปลี่ยนแปลงตัวแปรที่เพิ่งกล่าวถึง ในบทความเรื่อง “การเปลี่ยนแปลงของตัวแปรในปริพันธ์หลายส่วน” Ostrogradskiy เปิดเผยข้อผิดพลาดของ Lagrange และเป็นครั้งแรกที่นำเสนอวิธีการทางเรขาคณิตที่ชัดเจนสำหรับการแปลงตัวแปรในอินทิกรัลคู่ซึ่งในรูปแบบที่ค่อนข้างเข้มงวดกว่านั้นถูกนำเสนอใน คู่มือของเรา กล่าวคือ เมื่อเปลี่ยนตัวแปรในปริพันธ์ตามสูตร พื้นที่ของการรวมจะถูกหารด้วยเส้นพิกัดของทั้งสองระบบ u = const, v = const เป็นสี่เหลี่ยมโค้งขนาดเล็กที่สุด จากนั้นอินทิกรัลสามารถรับได้โดยการเพิ่มองค์ประกอบเหล่านั้นที่สอดคล้องกับแถบโค้งที่แคบอย่างไม่สิ้นสุดก่อนจากนั้นจึงรวมองค์ประกอบต่อไปด้วยแถบจนกว่าพวกมันจะหมด การคำนวณอย่างง่ายให้พื้นที่ที่สามารถถือได้ว่าเป็นสี่เหลี่ยมด้านขนานจนถึงลำดับที่สูงกว่าเล็กน้อย นิพจน์ โดยที่ จะถูกเลือกเพื่อให้พื้นที่นั้นเป็นค่าบวก ส่งผลให้เราได้สูตรที่รู้จักกันเป็นอย่างดี

สำหรับฟังก์ชันของตัวแปรสองตัวที่กำหนดเป็น z = NS(NS, y) .

อินทิกรัลคู่เขียนดังนี้:

ที่นี่ NS- ร่างแบนที่ล้อมรอบด้วยเส้นซึ่งนิพจน์ (ความเท่าเทียมกัน) ถูกกำหนดไว้ในการคำนวณอินทิกรัลคู่ ซ้ายและขวา - ความเท่าเทียมกันที่ตัวแปรทางด้านซ้าย NS, และด้านบนและด้านล่าง - ความเท่าเทียมกันที่ตัวแปรทางซ้ายคือ y... สถานที่นี้และต่อไป - หนึ่งในสิ่งที่สำคัญที่สุดสำหรับการทำความเข้าใจเทคนิคการคำนวณอินทิกรัลคู่

คำนวณอินทิกรัลคู่ - หมายถึง การหาจำนวนเท่ากับพื้นที่ของรูปดังกล่าว NS .

จนกว่าเราจะสัมผัส คำจำกัดความของอินทิกรัลคู่ แต่เราจะเรียนรู้การคำนวณมัน จะเข้าใจได้ง่ายขึ้นว่าอินทิกรัลคู่คืออะไรเมื่อคุณแก้ปัญหาหลายอย่างเพื่อคำนวณมัน ดังนั้นคุณจะพบคำจำกัดความของอินทิกรัลคู่ที่ส่วนท้ายของบทเรียนนี้ ก้าวไปข้างหน้าเล็กน้อย เราสามารถสังเกตได้เพียงว่าคำจำกัดความของอินทิกรัลคู่นั้นเกี่ยวข้องกับตัวเลขดังกล่าวด้วย NS .

ถ้ารูป NSเป็นรูปสี่เหลี่ยมผืนผ้า เส้นทั้งหมดที่ล้อมรอบเป็นเส้นตรง ถ้ารูป NS- เป็นเส้นโค้ง จากนั้นทางด้านซ้ายและด้านขวาล้อมรอบด้วยเส้นตรง และด้านบนและด้านล่าง - โดยเส้นโค้งที่กำหนดโดยความเท่าเทียมกันที่ให้ไว้ในงาน มีบางครั้งที่ตัวเลข NS- สามเหลี่ยม แต่เพิ่มเติมเกี่ยวกับกรณีดังกล่าวเล็กน้อย

ในการคำนวณอินทิกรัลคู่จึงจำเป็นต้องเรียงลำดับเส้นที่ล้อมรอบรูป NSซึ่งมีชื่อที่เข้มงวด - พื้นที่ของการบูรณาการ เรียงซ้ายขวาบนและล่าง สิ่งนี้จะต้องใช้เมื่อ การลดอินทิกรัลคู่ให้เป็นอินทิกรัลแบบวนซ้ำ - วิธีการคำนวณอินทิกรัลคู่

กรณีพื้นที่สี่เหลี่ยม:

กรณีพื้นที่โค้ง:

และนี่คือคำตอบของอินทิกรัลบางตัวที่เราคุ้นเคยอยู่แล้ว ซึ่งได้กำหนดขีดจำกัดบนและล่างของการรวมเข้าด้วยกัน นิพจน์ที่กำหนดเส้นที่ผูกกับรูปร่าง NSจะเป็นขีดจำกัดของการบูรณาการสำหรับอินทิกรัลแน่นอนธรรมดาที่เราเข้าใกล้แล้ว

การลดอินทิกรัลคู่เป็นอินทิกรัลซ้ำ

กรณีพื้นที่สี่เหลี่ยม

ให้ฟังก์ชันดังกล่าวมีอินทิกรัลคู่

ถึง คำนวณอินทิกรัลคู่นี้ จำเป็นต้องลดให้เป็นอินทิกรัลซ้ำซึ่งมีรูปแบบ

ก่อนอื่น คุณต้องคำนวณอินทิกรัลจำกัดวงใน (ขวา) จากนั้น - อินทิกรัลจำกัดวงนอก (ซ้าย)

เปลี่ยนบทบาทได้ NSและ y

ตัวอย่างที่ 1คำนวณอินทิกรัลคู่

เราคำนวณอินทิกรัลด้านใน (ขวา) โดยสมมติว่า y เป็นค่าคงที่ พวกเราได้รับ.

ตัวอย่างที่ 2คำนวณอินทิกรัลคู่

สารละลาย. ลดอินทิกรัลคู่นี้เป็นอินทิกรัลแบบวนซ้ำ

ในรูปวาดเราสร้างพื้นที่ของการบูรณาการ:

ตอนนี้เราคำนวณอินทิกรัลด้านนอก (ซ้าย) ของอินทิกรัลด้านใน (ขวา) ที่คำนวณได้:

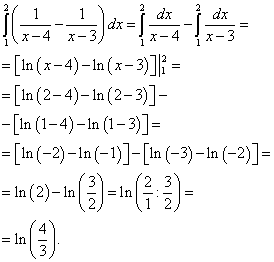
ผลลัพธ์จะเป็นคำตอบของอินทิกรัลคู่นี้

คำนวณอินทิกรัลสองเท่าด้วยตัวเองแล้วดูวิธีแก้ปัญหา

กรณีของพื้นที่โค้งหรือสามเหลี่ยม

กำหนดให้มีฟังก์ชันของตัวแปรสองตัวอีกครั้ง NS(NS, y) และข้อจำกัดสำหรับ NS: มีชนิดที่แตกต่างกันเล็กน้อยอยู่แล้ว:

รายการนี้หมายความว่าตัวเลข NSขอบซ้ายและขวาเช่นในกรณีของพื้นที่เป็นเส้นตรง - เส้นตรง NS = NSและ NS = NSแต่ด้านล่างและด้านบนเป็นเส้นโค้งที่กำหนดโดยสมการและ กล่าวอีกนัยหนึ่งและเป็นหน้าที่

ให้ฟังก์ชันดังกล่าวมีอินทิกรัลคู่ด้วย

ในการคำนวณอินทิกรัลคู่นี้ จำเป็นต้องลดให้เป็นอินทิกรัลซ้ำซึ่งมีรูปแบบ

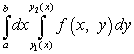นี่คือข้อ จำกัด ของการบูรณาการ NSและ NSเป็นตัวเลขและเป็นฟังก์ชัน ในกรณีของพื้นที่สามเหลี่ยม หนึ่งในฟังก์ชันหรือคือสมการของเส้นตรง กรณีนี้จะถูกวิเคราะห์ในตัวอย่างที่ 3

ในกรณีของพื้นที่เป็นเส้นตรง ก่อนอื่นคุณต้องคำนวณอินทิกรัลจำกัดสิทธิ์ที่ถูกต้องก่อน จากนั้นจึงคำนวณอินทิกรัลแน่นอนทางซ้าย

ในทำนองเดียวกัน คุณสามารถเปลี่ยนบทบาทได้ NSและ y... จากนั้นอินทิกรัลที่วนซ้ำจะมีรูปแบบ

อินทิกรัลที่เกิดซ้ำดังกล่าวจะต้องได้รับการแก้ไขในลักษณะเดียวกัน: อันดับแรก อินทิกรัลด้านใน (ขวา) จากนั้นอินทิกรัลด้านนอก (ซ้าย)

ตัวอย่างที่ 5คำนวณอินทิกรัลคู่

สารละลาย. ลดอินทิกรัลคู่นี้เป็นอินทิกรัลแบบวนซ้ำ

ในภาพวาด เราสร้างพื้นที่การรวมและเห็นว่าเป็นรูปสามเหลี่ยม:

เราคำนวณอินทิกรัลด้านใน (ขวา) โดยพิจารณา x ค่าคงที่ พวกเราได้รับ.

ตอนนี้เราคำนวณอินทิกรัลด้านนอก (ซ้าย) ของอินทิกรัลด้านใน (ขวา) ที่คำนวณได้ อันดับแรก เราแสดงอินทิกรัลนี้เป็นผลรวมของอินทิกรัล:

เราคำนวณเทอมแรก:

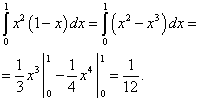
เราคำนวณเทอมที่สอง:

เราคำนวณเทอมที่สาม:

เราได้ผลรวม ซึ่งจะเป็นคำตอบของอินทิกรัลคู่นี้:

ตัวอย่างที่ 6คำนวณอินทิกรัลคู่

สารละลาย. ลดอินทิกรัลคู่นี้เป็นอินทิกรัลแบบวนซ้ำ

ในรูปวาดเราสร้างพื้นที่ของการบูรณาการ:

เราคำนวณอินทิกรัลด้านใน (ขวา) โดยพิจารณา x ค่าคงที่ พวกเราได้รับ.

ผลลัพธ์จะเป็นคำตอบของอินทิกรัลคู่นี้

NS- ถูกต้องและไม่ถูกต้อง y- โดเมนการรวมที่ถูกต้องและไม่ถูกต้อง

มันเกิดขึ้นที่ขอบเขตของการรวมตัวของอินทิกรัลคู่ถูกล้อมรอบด้วยเส้นดังกล่าวซึ่งจำเป็นต้องแยกขอบเขตของการรวมออกเป็นส่วน ๆ และแก้ปัญหาอินทิกรัลวนซ้ำที่เกี่ยวข้องกันแยกจากกัน กรณีเหล่านี้คือเมื่อ:

1) พื้นที่ของการรวมเป็นตัวเลขที่มีเส้นตรงหรือเส้นโค้งตั้งแต่สองเส้นขึ้นไปในรูปแบบของเส้นขอบล่างหรือบน (ซ้ายหรือขวา)

2) พื้นที่ของการรวมเป็นตัวเลข เส้นขอบที่เส้นตรงตัดกันที่จุดมากกว่าสองจุด

หากข้างต้นใช้กับเส้นขอบด้านซ้ายหรือด้านขวาของขอบเขตการรวม นั่นคือ ข้อจำกัดที่กำหนดโดยเส้นที่แสดงในรูปของ NSจากนั้นภูมิภาคของการบูรณาการจะเรียกว่า NS-ผิด. ถ้าตรง y = y0 ตัดขอบที่สอดคล้องกันที่จุดเดียวและถ้าเส้นตรงหรือเส้นโค้งเพียงเส้นเดียวทำหน้าที่เป็นขอบเขต พื้นที่ของการรวมจะถูกเรียกว่า NS- ถูกต้อง

ในทำนองเดียวกัน หากเส้นขอบที่กำหนดโดยเส้นที่แสดงผ่าน y, ตรง NS = NS0 ตัดกันที่จุดมากกว่าหนึ่งจุดหรือถ้าเส้นตรงหรือเส้นโค้งมากกว่าหนึ่งเส้นทำหน้าที่เป็นเขตแดนจะเรียกว่าขอบเขตของการรวม y-ผิด. แสดงป้ายเลย y- พื้นที่ที่ถูกต้องน่าจะค่อนข้างง่าย

จนถึงตอนนี้ เราได้ดูตัวอย่างกับ NS- ไม่ถูกต้องและ y- พื้นที่ที่ถูกต้องของการบูรณาการ ทีนี้มาพิจารณากรณีที่เงื่อนไขความถูกต้องถูกละเมิด

ตัวอย่างที่ 7คำนวณอินทิกรัลคู่ พื้นที่การรวมที่ล้อมรอบด้วยเส้น y = NS , xy = 1 , y = 2 .

สารละลาย. พื้นที่ของการบูรณาการคือ y-ผิด เนื่องจากไม่สามารถกำหนดขอบเขตล่างด้วยบรรทัดเดียวได้ y = y(NS) ... ดังที่คุณเห็นในภาพด้านบน เส้นขอบล่างประกอบด้วย y = NS(เบอร์กันดีสีเข้ม) และ xy= 1 (สีเขียว) ดังนั้นโดยตรง NS= 1 (สีดำ) เราสามารถแบ่งขอบเขตของการรวมเป็นสองส่วน - และ

อินทิกรัลคู่นี้คำนวณได้ดังนี้:

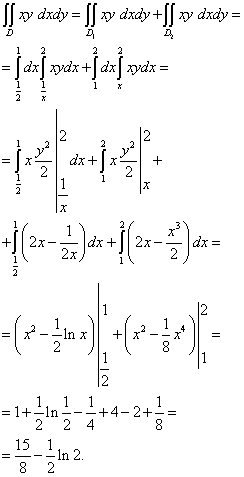
การเปลี่ยนลำดับการบูรณาการ

ดังที่กล่าวไว้ข้างต้น หลังจากลดอินทิกรัลคู่ให้เป็นอินทิกรัลแบบวนซ้ำแล้ว เราสามารถเปลี่ยนตัวแปรได้ NSและ yบทบาทหรือกล่าวอีกนัยหนึ่งเปลี่ยนลำดับของการบูรณาการ

การเปลี่ยนแปลงลำดับของการบูรณาการสามารถอธิบายเป็นรูปเป็นร่างโดยคำต่อไปนี้เกี่ยวกับ "เฮนรี่:" นี่คือพฤติกรรมของคนที่อาศัยอยู่ในป่า - สัตว์ร้ายครั้งหนึ่งในกรงและนี่คือพฤติกรรมของผู้อยู่อาศัยในกรง - ผู้ชายหลงทาง ป่าแห่งความสงสัย " และเช่นเดียวกัน: "ชาลเมอร์ฉีกจดหมายเป็นชิ้นเล็กที่สุดพันชิ้นและเริ่มฉีกพรมราคาแพงของเขาเดินไปมา" ( O.Henry. เชเฮราซาดแห่งเมดิสันสแควร์.)

แล้วถ้าเรามีอินทิกรัลด้านซ้ายเทียบกับตัวแปร NS, และอันที่ถูกต้อง - by yหลังจากเปลี่ยนลำดับการผสานรวมแล้ว ทุกอย่างจะกลับกัน จากนั้นขีดจำกัดของการผสานรวมสำหรับเกม "ใหม่" ควร "ยืม" จาก "เก่า" x และขีดจำกัดของการผสานรวมสำหรับ "ใหม่" x ควรได้รับในแบบฟอร์ม ฟังก์ชันผกผันโดยการแก้สมการของ x ซึ่งกำหนดขีด จำกัด สำหรับเกม

ตัวอย่างที่ 8

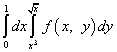สารละลาย. หลังจากเปลี่ยนลำดับของการบูรณาการ อินทิกรัลเหนือเกมจะกลายเป็นทางซ้าย และอินทิกรัลบน x จะกลายเป็นทางขวา ขีดจำกัดของการรวมสำหรับเกม "ใหม่" จะถูกยืมมาจาก "เก่า" x นั่นคือ ขีดจำกัดล่างเท่ากับศูนย์ และขีดจำกัดบนเท่ากับหนึ่ง ขีด จำกัด ของการบูรณาการสำหรับเกม "เก่า" นั้นมาจากสมการและ เมื่อแก้สมการเหล่านี้สำหรับ x แล้ว เราได้รับขีดจำกัดใหม่ของการรวมสำหรับ x:

(ล่าง) และ (บน)

ดังนั้น หลังจากเปลี่ยนลำดับการรวม อินทิกรัลที่ซ้ำกันจะถูกเขียนดังนี้:

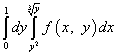หลังจากเปลี่ยนลำดับของการบูรณาการในอินทิกรัลคู่แล้ว พื้นที่การรวมมักจะกลายเป็น y-ผิดหรือ NS- ไม่ถูกต้อง (ดูย่อหน้าก่อนหน้า) จากนั้นจึงจำเป็นต้องแบ่งขอบเขตของการรวมออกเป็นส่วนๆ และแก้อินทิกรัลที่มีการวนซ้ำที่สอดคล้องกันแต่ละส่วนแยกกัน

เนื่องจากการแบ่งพื้นที่การบูรณาการออกเป็นส่วน ๆ ทำให้เกิดปัญหาบางอย่างสำหรับนักเรียนหลายคน เราจะไม่จำกัดตัวเองอยู่เพียงตัวอย่างที่ให้ไว้ในย่อหน้าก่อนหน้า แต่ให้พิจารณาตัวอย่างเพิ่มเติมสองสามตัวอย่าง

ตัวอย่างที่ 9เปลี่ยนลำดับของการรวมสำหรับ re-integral

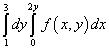สารละลาย. ดังนั้น พื้นที่ของการรวมตัวของอินทิกรัลที่มีการวนซ้ำนี้ถูกล้อมรอบด้วยเส้นตรง y = 1 , y = 3 , NS = 0 , NS = 2y .

เมื่อรวมเข้าด้วยกันในลำดับที่ต่างกัน ขอบล่างของพื้นที่ประกอบด้วยเส้นตรงสองเส้น: ABและ BCซึ่งได้จากสมการ y= 1 และ y = NS/ 2 ซึ่งสามารถเห็นได้ในรูปด้านล่าง

ทางออกจากความไม่แน่นอนนี้คือการแบ่งขอบเขตการรวมออกเป็นสองส่วน พื้นที่รวมจะถูกหารด้วยเส้นตรง BM... เราคำนวณขีดจำกัดใหม่ของการรวมโดยค้นหาฟังก์ชันผกผัน ตามวิธีแก้ปัญหานี้ อินทิกรัลแบบวนซ้ำหลังจากเปลี่ยนลำดับการรวมจะเท่ากับผลรวมของอินทิกรัลสองตัว:

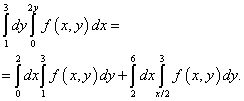
โดยธรรมชาติแล้ว จะเป็นการแก้ปัญหาของอินทิกรัลคู่ ซึ่งจะลดจำนวนลงเป็นอินทิกรัลแบบวนซ้ำที่ให้ไว้ในเงื่อนไขของตัวอย่างนี้

ตัวอย่างที่ 10เปลี่ยนลำดับของการรวมสำหรับ re-integral

สารละลาย. ดังนั้น พื้นที่ของการรวมตัวของอินทิกรัลแบบวนซ้ำนั้นถูกล้อมรอบด้วยเส้นตรง NS = 0 , NS= 2 และเส้นโค้งและ.

ดังที่เห็นในภาพด้านล่าง เส้นตรงขนานกับแกน 0xจะข้ามขอบเขตล่างของภูมิภาคการรวมที่มากกว่าสองจุด

ดังนั้น เราจะแบ่งขอบเขตของการรวมออกเป็นสามส่วนด้วยเส้นตรงซึ่งวาดด้วยสีดำในรูป เราคำนวณขีดจำกัดใหม่ของการรวมโดยค้นหาฟังก์ชันผกผัน ข้อจำกัดสำหรับสามด้านใหม่ของการรวมกลุ่มจะเป็นดังนี้

ตามวิธีแก้ปัญหานี้ อินทิกรัลแบบวนซ้ำหลังจากเปลี่ยนลำดับการรวมจะเท่ากับผลรวมของอินทิกรัลสามตัว:

ผลรวมของอินทิกรัลสามตัวที่เท่ากันจะเท่ากับอินทิกรัลคู่ ซึ่งลดเหลืออินทิกรัลแบบวนซ้ำที่ให้ไว้ในเงื่อนไขของตัวอย่างนี้

และถึงกระนั้น เหตุสุดวิสัยมักรบกวนนักเรียนในขั้นตอนก่อนหน้านี้ นั่นคือการกำหนดขอบเขตของการบูรณาการ ความวิตกกังวลและความสับสนไม่ได้เกิดขึ้นโดยไร้เหตุผล: หากโดยปกติแล้วการดูภาพวาดเพื่อแยกขอบเขตการรวมออกเป็นส่วนๆ และเพื่อแก้ไขอินทิกรัลที่เกิดซ้ำ - ตารางของปริพันธ์ จำเป็นต้องมีประสบการณ์การฝึกอบรมในการกำหนดขีดจำกัดการผสานรวม . เรามาดูตัวอย่างกัน โดยเราจะเน้นเฉพาะการจัดเรียงขีดจำกัดของการผสานรวม และเกือบจะโดยอัตโนมัติในพาร์ติชันของโดเมนและละเว้นโซลูชันนั้นเอง

ตัวอย่างที่ 11หาขีดจำกัดของการบูรณาการของอินทิกรัลคู่ถ้าขอบเขตของการบูรณาการ NSกำหนดไว้ดังนี้

y - 2NS ≤ 0;
2ปี - NS ≥ 0;
xy ≤ 2.

สารละลาย. อย่างชัดเจน (ผ่าน NSและ y"ปราศจากสิ่งเจือปน") ไม่ได้ระบุเส้นที่ล้อมรอบขอบเขตของการรวมเข้าด้วยกัน เนื่องจากสำหรับ x พวกเขามักจะกลายเป็นเส้นตรงที่สัมผัสที่จุดหนึ่งขอบเขตบนและล่างที่แสดงผ่านเกม จากนั้นเราจะไปตามเส้นทางนี้อย่างแน่นอน ยิ่งกว่านั้น เมื่อเปลี่ยนลำดับของการบูรณาการ เราจะได้ภูมิภาคการรวมที่มีพื้นที่เดียวกัน มาแก้ความไม่เท่าเทียมกันเกี่ยวกับเกมและรับ:

y ≤ 2NS;
y ≥ NS/2;
y ≤ 2/NS.

เราสร้างเส้นผลลัพธ์ในรูปวาด ขีด จำกัด ของ x-integration เป็นเส้นจริง NS= 0 และ NS= 2 แต่พื้นที่ของการบูรณาการกลับกลายเป็น y-ผิด เนื่องจากไม่สามารถกำหนดเส้นขอบบนด้วยบรรทัดเดียวได้ y = y(NS) .

ดาวน์โหลดจาก Depositfiles

บรรยาย 5-6

หัวข้อ2. อินทิกรัลหลายตัว

อินทิกรัลคู่

คำถามควบคุม

1. ปริพันธ์สองเท่า ความหมายทางเรขาคณิตและทางกายภาพ

2. คุณสมบัติของอินทิกรัลคู่

3. การคำนวณอินทิกรัลคู่ในพิกัดคาร์ทีเซียน

4. การเปลี่ยนแปลงของตัวแปรในอินทิกรัลคู่ การคำนวณอินทิกรัลคู่ในพิกัดเชิงขั้ว

ให้ฟังก์ชั่น z = NS (NS , y) ถูกกำหนดไว้ในเขตปิดขอบเขต NSเครื่องบิน. มาแบ่งพื้นที่กัน NSโดยพลการใน NSเขตปิดเบื้องต้น  1 , … , NSกับพื้นที่   1 , …,   NSและเส้นผ่านศูนย์กลาง NS 1 , …, NS NS ตามลำดับ เราแสดงว่า NSเส้นผ่านศูนย์กลางที่ใหญ่ที่สุดของภูมิภาค  1 , … ,  NS... ในทุกพื้นที่  kเลือกจุดใดก็ได้ NS k (NS k , y k) และเขียน ผลรวมปริพันธ์การทำงาน NS(x, y)

NS =
(1)

คำนิยาม. อินทิกรัลคู่การทำงาน NS(x, y) ตามพื้นที่ NSเรียกว่า ลิมิตของผลรวมปริพันธ์

, (2)

ถ้ามันมีอยู่

ความคิดเห็น ผลรวมปริพันธ์ NSขึ้นอยู่กับการแบ่งภูมิภาค NSและการเลือกจุด NS k (k=1, …, NS). อย่างไรก็ตาม ขีดจำกัด
หากมีอยู่แล้วไม่ขึ้นกับวิธีการแบ่งเขต NSและการเลือกจุด NS k .

เงื่อนไขที่เพียงพอสำหรับการมีอยู่ของอินทิกรัลคู่ อินทิกรัลคู่ (1) มีอยู่ถ้าฟังก์ชัน NS(x, y) ต่อเนื่องใน NSยกเว้นส่วนโค้งเรียบเป็นชิ้นๆ จำนวนจำกัด และมีขอบเขตเป็น NS... ต่อไปนี้ เราจะถือว่าอินทิกรัลคู่ทั้งหมดที่อยู่ระหว่างการพิจารณามีอยู่

ความหมายทางเรขาคณิตของอินทิกรัลคู่

ถ้า NS(x, y) ≥0ในพื้นที่ NSจากนั้นอินทิกรัลคู่ (1) จะเท่ากับปริมาตรของตัว "ทรงกระบอก" ที่แสดงในรูป:

วี =
(3)

ร่างกายทรงกระบอกล้อมรอบด้วยพื้นที่ด้านล่าง NS, จากข้างบน  ส่วนหนึ่งของพื้นผิว z = NS (NS , y) ที่ด้านข้าง  โดยส่วนของเส้นแนวตั้งที่เชื่อมต่อขอบเขตของพื้นผิวนี้กับภูมิภาค NS.

ความหมายทางกายภาพของอินทิกรัลคู่ มวลแผ่นแบน

ให้จานแบนๆ NSด้วยฟังก์ชันความหนาแน่นที่รู้จัก γ ( NS,ที่) แล้วแยกเพลท D ออกเป็นส่วน D ผมและเลือกคะแนนตามอำเภอใจ
, เราได้รับสำหรับมวลแผ่น
หรือเปรียบเทียบกับสูตร (2):

(4)

4. คุณสมบัติบางอย่างของอินทิกรัลคู่

ความเป็นลิเนียร์ถ้า กับเป็นค่าคงที่ตัวเลข ดังนั้น

สารเติมแต่งถ้าพื้นที่ NS "แบ่ง" ออกเป็นพื้นที่ NS 1 และ NS 2 แล้ว

3) พื้นที่พื้นที่จำกัด NSเท่ากับ

(5)

การคำนวณอินทิกรัลคู่ในพิกัดคาร์ทีเซียน

ให้ภูมิภาคได้รับ

รูปที่ 1

ด = { (NS , y ): ≤ x ≤ b , φ 1 (NS ) ≤ y≤ φ 2 (NS ) } (6)

ภาค NS อยู่ในแถบระหว่างเส้นตรง NS = NS , y = NSจากด้านล่างและจากด้านบนมีขอบเขตตามลำดับโดยเส้นโค้ง y = φ 1 (NS ) และ y = φ 2 (NS ) .

ปริพันธ์สองเท่า (1) เหนือพื้นที่ NS(4) คำนวณโดยส่งผ่านไปยังอินทิกรัลแบบวนซ้ำ:

(7)

อินทิกรัลแบบวนซ้ำนี้คำนวณได้ดังนี้ ขั้นแรกให้คำนวณอินทิกรัลภายใน

ตามตัวแปร y, โดยที่ NSถือว่าคงที่ ผลลัพธ์คือฟังก์ชันของตัวแปร NSจากนั้นจึงคำนวณอินทิกรัล "นอก" ของฟังก์ชันนี้เทียบกับตัวแปร NS .

ความคิดเห็น กระบวนการส่งผ่านไปยังอินทิกรัลแบบวนซ้ำตามสูตร (7) มักเรียกว่าการจัดเรียงลิมิตของการผสานรวมในอินทิกรัลคู่ เมื่อกำหนดขีดจำกัดของการผสานรวม ควรคำนึงถึงสองประเด็น ประการแรก ขีดจำกัดล่างของการผสานไม่ควรเกินขีดจำกัดบน ประการที่สอง ขีดจำกัดของอินทิกรัลภายนอกควรคงที่ และอินทิกรัลภายในโดยทั่วไปควรขึ้นอยู่กับตัวแปรของการผสานรวมของอินทิกรัลภายนอก

ตอนนี้ให้ภูมิภาค NSมีรูปแบบ

ด = { (NS , y ) : ค ≤ y ≤ d , ψ 1 (y ) ≤ x ≤ ψ 2 (y ) } . (8)

แล้ว

. (9)

สมมุติว่าพื้นที่ NSสามารถแสดงในรูปแบบ (6) และ (8) พร้อมกันได้ แล้วความเท่าเทียมกัน

(10)

ข้อความจากอินทิกรัลที่วนซ้ำหนึ่งไปยังอีกอันหนึ่งในความเท่าเทียมกัน (10) เรียกว่า เปลี่ยนลำดับการบูรณาการในอินทิกรัลคู่

ตัวอย่าง.

1) เปลี่ยนลำดับของการบูรณาการในปริพันธ์

สารละลาย. จากรูปแบบของอินทิกรัลแบบวนซ้ำ เราพบพื้นที่

ด = { (NS , y ): 0 ≤ x ≤ 1, 2 x ≤ y≤ 2 } .

มาวาดพื้นที่กันเถอะ NS... จากรูปจะเห็นว่าบริเวณนี้อยู่ในแถบแนวนอนระหว่างเส้นตรง y =0, y= 2 และระหว่างบรรทัด NS =0 และ NS= ด

บางครั้งตัวแปรจะเปลี่ยนไปเพื่อทำให้การคำนวณง่ายขึ้น:

,
(11)

ถ้าฟังก์ชัน (11) นั้นหาอนุพันธ์ได้อย่างต่อเนื่องและดีเทอร์มีแนนต์ (จาโคเบียน) ไม่เป็นศูนย์ในโดเมนที่พิจารณา:

(12)

กระทรวงศึกษาธิการและวิทยาศาสตร์แห่งสหพันธรัฐรัสเซีย

หลักสูตรการทำงาน

วินัย: คณิตศาสตร์ที่สูงขึ้น

(การเขียนโปรแกรมเชิงเส้นพื้นฐาน)

ในหัวข้อ: MULTIPLE INTEGRALS

สมบูรณ์: ______________

ครู:___________

วันที่ ___________________

ระดับ _________________

ลายเซ็น ________________

VORONEZH 2008

1 อินทิกรัลพหุคูณ

1.1 ปริพันธ์สองเท่า

1.2 อินทิกรัลสามเท่า

1.3 อินทิกรัลหลายตัวในพิกัดโค้ง

1.4 การประยุกต์ทางเรขาคณิตและทางกายภาพของอินทิกรัลหลายตัว

2 อินทิกรัลโค้งและพื้นผิว

2.1 อินทิกรัลโค้ง

2.2 อินทิกรัลพื้นผิว

2.3 การประยุกต์ทางเรขาคณิตและทางกายภาพ

บรรณานุกรม

1 อินทิกรัลพหุคูณ

1.1 อินทิกรัลคู่

พิจารณาในระนาบ Oxy พื้นที่ปิด D ที่ล้อมรอบด้วยเส้น L เราแบ่งเขตนี้ด้วยเส้นบางเส้นออกเป็น n ส่วน

และระยะทางที่ใหญ่ที่สุดที่สอดคล้องกันระหว่างจุดในแต่ละส่วนเหล่านี้จะแสดงด้วย d 1, d 2, ..., d n มาเลือกจุด Р ฉัน ในแต่ละส่วนกัน

ให้ฟังก์ชัน z = f (x, y) ถูกกำหนดในโดเมน D ให้เราแสดงด้วย f (P 1), f (P 2),…, f (P n) ค่าของฟังก์ชันนี้ที่จุดที่เลือกและเขียนผลรวมของผลิตภัณฑ์ในรูปแบบ f (P i) ΔS i :

, (1)

เรียกว่าผลรวมอินทิกรัลสำหรับฟังก์ชัน f (x, y) ในโดเมน D

หากมีข้อ จำกัด เดียวกันของผลรวมครบถ้วน (1) สำหรับ

และซึ่งไม่ได้ขึ้นอยู่กับวิธีการแบ่งโดเมน D ออกเป็นส่วน ๆ หรือการเลือกจุด P i ในนั้นจึงเรียกว่าอินทิกรัลคู่ของฟังก์ชัน f (x, y) เหนือโดเมน D และ แสดงว่า

. (2)

การคำนวณอินทิกรัลคู่บนพื้นที่ D ที่ล้อมรอบด้วยเส้น

x = ก, x = ข (a< b), где φ 1 (х) и φ 2 (х) непрерывны на (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:

(3)

1.2 อินทิกรัลสามเท่า

แนวคิดของอินทิกรัลสามตัวถูกนำมาใช้โดยการเปรียบเทียบกับอินทิกรัลคู่

ให้บางโดเมน V ถูกกำหนดในอวกาศที่ล้อมรอบด้วยพื้นผิวปิด S ให้เรากำหนดฟังก์ชันต่อเนื่อง f (x, y, z) ในโดเมนปิดนี้ จากนั้นเราแบ่งพื้นที่ V ออกเป็นส่วนใดก็ได้ Δv i โดยสมมติว่าปริมาตรของแต่ละส่วนเท่ากับ Δv i และประกอบรวมอินทิกรัลของแบบฟอร์ม

, (4)

จำกัดที่

ผลรวมปริพันธ์ (11) ซึ่งไม่ได้ขึ้นอยู่กับวิธีการแบ่งโดเมน V และการเลือกจุด P i ในแต่ละโดเมนย่อยของโดเมนนี้ เรียกว่าอินทิกรัลสามส่วนของฟังก์ชัน f (x, y, z) เหนือ โดเมน V:

. (5)

อินทิกรัลสามเท่าของฟังก์ชัน f (x, y, z) ส่วนภูมิภาค V เท่ากับอินทิกรัลสามเท่าในบริเวณเดียวกัน:

. (6)

1.3 อินทิกรัลหลายตัวในพิกัดโค้ง

ให้เราแนะนำพิกัดโค้งบนระนาบที่เรียกว่าพิกัดเชิงขั้ว ให้เราเลือกจุด O (ขั้ว) และรังสีที่โผล่ออกมาจากจุดนั้น (แกนขั้ว)

ข้าว. มะเดื่อ 2 3

พิกัดของจุด M (รูปที่ 2) จะเป็นความยาวของส่วน MO - รัศมีเชิงขั้ว ρ และมุม φ ระหว่าง MO กับแกนขั้วโลก: M (ρ, φ) โปรดทราบว่าสำหรับทุกจุดของระนาบ ยกเว้นขั้ว ρ> 0 และมุมขั้ว φ จะถือเป็นค่าบวกเมื่อวัดในทิศทางทวนเข็มนาฬิกาและค่าลบเมื่อวัดในทิศทางตรงกันข้าม

ความสัมพันธ์ระหว่างพิกัดเชิงขั้วและพิกัดคาร์ทีเซียนของจุด M สามารถกำหนดได้โดยการจัดตำแหน่งจุดกำเนิดของระบบพิกัดคาร์ทีเซียนกับขั้ว และแกนครึ่งแกนบวก Ox - กับแกนขั้วโลก (รูปที่ 3) จากนั้น x = ρcosφ, у = ρsinφ จากที่นี่

, ทีจี.

ในโดเมน D ล้อมรอบด้วยเส้นโค้ง ρ = Φ 1 (φ) และ ρ = Φ 2 (φ) โดยที่ φ 1< φ < φ 2 , непрерывную функцию z = f(φ, ρ) (рис. 4).

(7)

ในพื้นที่สามมิติ พิกัดทรงกระบอกและทรงกลมจะถูกป้อน

พิกัดทรงกระบอกของจุด P (ρ, φ, z) คือพิกัดเชิงขั้ว ρ, φ ของการฉายภาพของจุดนี้บนระนาบ Oxy และจุดประยุกต์ของจุดนี้ z (รูปที่ 5)

รูปที่ 5 รูปที่ 6

สูตรสำหรับการเปลี่ยนจากพิกัดทรงกระบอกเป็นพิกัดคาร์ทีเซียนสามารถระบุได้ดังนี้:

x = ρcosφ, y = ρsinφ, z = z (แปด)

ในพิกัดทรงกลม ตำแหน่งของจุดในอวกาศถูกกำหนดโดยพิกัดเชิงเส้น r - ระยะห่างจากจุดถึงจุดกำเนิดของระบบพิกัดคาร์ทีเซียน (หรือขั้วของระบบทรงกลม), φ - มุมขั้วระหว่างขั้วบวก ครึ่งแกน Ox และการฉายของจุดบนระนาบ Oxy และ θ - มุมระหว่างเซมิแกนบวกของแกน Оz และเซ็กเมนต์ OP (รูปที่ 6) โดยที่

ให้เรากำหนดสูตรสำหรับการเปลี่ยนจากพิกัดทรงกลมเป็นพิกัดคาร์ทีเซียน:

x = rsinθcosφ, y = rsinθsinφ, z = rcosθ (เก้า)

จากนั้นสูตรสำหรับการเปลี่ยนไปใช้พิกัดทรงกระบอกหรือทรงกลมในอินทิกรัลสามชั้นจะมีลักษณะดังนี้: