व्याख्यान एकाधिक अभिन्न, दुहेरी अभिन्न. दुहेरी इंटिग्रल्सची गणना: सिद्धांत आणि उदाहरणे एकाधिक इंटीग्रल्स सोडवणे

Def . असू द्या ,
,

.

सेटला क्लोज्ड गॅप किंवा क्लोज्ड बार इन असे म्हणतात .

सेटला ओपन गॅप म्हणतात

किंवा आत एक ओपन बार .

Def . अंतरांचे मोजमाप आणि प्रमाण म्हणतात:

(अधिक तंतोतंत
).

Def . तर
असे की
मग मध्यांतर त्याला अध: पतन आणि म्हणतात
.

अंतर मोजण्याचे गुणधर्म:

अ). सकारात्मकता:
, आणि
जर आणि फक्त जर - अध: पतित आहे.

ब). सकारात्मक एकरूपता:.

v). अॅडिटिव्हिटी:

* च्या साठी
असे की
;

* च्या साठी
आणि

.

जी). मोजमापाची नीरसता:.

Def . बारचा व्यास (अंतर) हे मूल्य आहे:

लक्षात ठेवा की
आणि
समान गोष्टी नाहीत. उदाहरणार्थ, जर - नंतर अध: पतन
, अ
(साधारणतः बोलातांनी).

ज्यात: *;

* ;*
.

Def . एकूण
उप-अंतर मध्यांतर विभाजित करणे म्हणतात , तर: *;

*
; *
; *
; *
.

प्रमाण
विभाजन मापदंड म्हणतात पी(ज्यात
).

Def . विभाजन विभाजन परिष्कृत करणे म्हणतात जर विभाजनाचे सर्व घटक विभाजित घटक विभाजित करून प्राप्त .

हे सूचित केले आहे:
... वाचा: लहान किंवा मोठा .

मोठ्या-लहान नात्यासाठी, हे खरे आहे:

*. संक्रमणशीलता -; *.
;

*.

; *.

|
.

. एकाधिक अभिन्न व्याख्या

असू द्या
- लाकूड (अंतर) मध्ये ,
- अंतर विभागणे मी... विभाजनाच्या प्रत्येक अंतराने बिंदू चिन्हांकित करा
.

आम्हाला मिळते
साठी चिन्हांकित गुणांसह विभाजित करा
.

प्रमाण
फंक्शनसाठी अविभाज्य Riemann बेरीज म्हणतात f (x) मध्यांतर मी चिन्हांकित गुणांसह विभाजित करून
.

Def :
=
=
.

सूचित करणे - बारवर समाकलित फंक्शन्सचा संच मी आम्ही लिहितो:

Def : ε > 0 δ>0<.

जर फंक्शनसाठी f(x) वर मीआणि विभाजन
- द्वारे दर्शवा
- फंक्शनचे सर्वोच्च आणि सर्वात कमी मूल्य f(x) वर मी केमग प्रमाण
=
आणि
=
त्यांना लोअर आणि अप्पर डार्बॉक्स बेरीज म्हणतात.

§. एकाधिक अविभाज्य अस्तित्वासाठी डार्बॉक्स निकष.

ट 0 . कार्य करण्यासाठी
बारवर समाकलित होते (त्या.
) आवश्यक आणि पुरेसे आहे

. Δ▲.

युक्लिडियन स्पेसमधील बारवरील फंक्शनचे एकत्रीकरण निश्चित केले जाते. युक्लिडियन स्पेसमधून अनियंत्रित बाउंड सेटवर फंक्शन कसे समाकलित करावे?

चला फंक्शनचे इंटिग्रल परिभाषित करूया f सेट द्वारे
.

Def : असू द्या
आणि
- मर्यादित, म्हणजे
... कार्य
सेटचे वैशिष्ट्यपूर्ण कार्य म्हणतात एम.

मग:
≡
.

संचावर अविभाज्यची व्याख्या कोणत्या पट्टीवर आहे यावर अवलंबून नाही एमनिवडलेले, म्हणजे

.

याचा अर्थ असा की एका संचावर अविभाज्य ची व्याख्या बरोबर आहे.

एकत्रीकरणासाठी आवश्यक अट.कार्य करण्यासाठी f(x) वर एमसमाकलित व्हा, हे आवश्यक आहे f(xपर्यंत मर्यादित होते एम. Δ▲.

. एकाधिक समाकलनाचे गुणधर्म.

1  . Linearity: अनेक आर एमसेटवर एकीकृत कार्ये एम -रेषीय

जागा, आणि
- रेखीय कार्यात्मक.

2  . सामान्यीकरण स्थिती:
... नोटेशनचे आणखी एक रूप
खरं तर युक्लिडियन स्पेसमधून अनियंत्रित संचाचे माप ठरवते.

3  . जर लेबेस्ग्यू मापनाच्या शून्यावर अविभाज्य शून्य अस्तित्वात असेल तर ते

शून्य आहे.

टीप:बरेच एमत्याला लेबेस्ग्यू माप शून्य म्हणतात,

तर

असे की
आणि
.

4  . a.;ब;

vतर
आणि - शून्यापासून विभक्त एम, नंतर

5  .
आणि f=g p.c. (जवळजवळ सर्वत्र) चालू एम, नंतर
.

6  . अतिरिक्तता: जर
आणि
नंतर

सामान्यतः:
.

. समानतेचे अनुसरण करते:

7  . मोनोटोन:
आणि
नंतर
.

8  . असमानतेचे एकत्रीकरण: जर
ito

9  . असू द्या

... ला
, हे आवश्यक आणि पुरेसे आहे की सेटचा आतील बिंदू आहे एम, ज्यात f (x)> 0 आणि सतत आहे.

10  . फंक्शनच्या मॉड्यूलची समाकलितता:
.

11  . सरासरी प्रमेय:
,
चालू एमचिन्ह जतन करते आणि
, नंतर

जर सेट एम- जोडलेले आणि f(x) चालू आहे
नंतर
असे की
.

12  . गैर-functionणात्मक कार्याचे समाकलन 0 च्या बरोबरीने होण्यासाठी

आवश्यक आणि पुरेसे f(x) = 0 जवळजवळ सर्वत्र एम.

13  . फुबिनीचे प्रमेय.दुहेरी अभिन्न साठी:

प्रदेश द्या
- आयत :. नंतर, अंतर्गत एकल समाकलनाच्या अस्तित्वाच्या अटीनुसार, दुहेरी अविभाज्य शोधण्यासाठी, एखादी व्यक्ती पुन्हा एकीकरणासाठी पुढे जाऊ शकते (चित्र पहा. A):

, किंवा

ई

एकत्रीकरणाचे डोमेन आयताकृती नसल्यास, फुबिनीचे प्रमेय अद्याप वैध आहे आणि त्याचे स्वरूप आहे (चित्र पहा. ब):

. (*)

टीप:एकीकरणाच्या बाह्य मर्यादा स्थिर असाव्यात, एकात्मतेची अंतर्गत मर्यादा ज्या व्हेरिएबलवर अजून एकत्रीकरण करायचे आहे त्यावर अवलंबून असू शकते.

सेटचे वैशिष्ट्यपूर्ण कार्य वापरून फॉर्म्युला (*) मिळवता येतो डी.

एकाधिक अभिन्न साठी:

युक्लिडियन स्पेसचे काही उपसमूह द्या आणि ... आम्ही या संचांचे कार्टेशियन उत्पादन परिभाषित करतो, जे यूक्लिडियन जागेचा उपसंच आहे
:.

मग Fubini च्या प्रमेय
असे दिसते आहे की:
.

प्रमेय बारसाठी देखील वैध आहे Xआणि वाय, आणि अधिक जटिल संरचनांसाठी.

उदाहरणे:

1 0 . गणना करा
जर प्रदेशाची सीमा
समीकरणांद्वारे दिले:

... प्रदेशाची सीमा निश्चित करणाऱ्या वक्रांचे छेदनबिंदू शोधणे, आम्हाला दोन गुण मिळतात:

आणि

... मग पुनरावृत्ती केलेल्या समाकलनाकडे जाताना एकात्मतेच्या मर्यादांची संभाव्य व्यवस्था देते:

अ).
;

0 . री-इंटिग्रलमध्ये एकत्रीकरणाचा क्रम बदला:

–

कृती:दुहेरी इंटिग्रलमध्ये एकीकरणाच्या मर्यादा सेट करताना, एकीकरणाच्या बाह्य मर्यादांसह प्रारंभ करण्याची शिफारस केली जाते.

0 . गणना करा:

, तर

पुनरावृत्त इंटिग्रल्स पास करणे देते:
.

या प्रकरणात, ट्रिपल इंटिग्रलमध्ये, मर्यादांची व्यवस्था एकीकरणाच्या अंतर्गत मर्यादांपासून सुरू होणे आवश्यक आहे. नंतर क्षेत्र प्रोजेक्ट करा व्हीविमानात xOy

परिसरात मर्यादा निश्चित करणे डी- विमानात पडलेले xOy.

4 0 . री-इंटिग्रलमध्ये एकत्रीकरणाचा क्रम बदला:
.

आपण Ostrogradskii च्या अनेक इंटीग्रल्सवरील कामांवर थोडे अधिक तपशीलवार विचार करूया.

ट्रिपल इंटिग्रलला डबल इंटिग्रलमध्ये रूपांतरित करण्यासाठी ओस्ट्रोग्राडस्कीचे सूत्र, जे आपण सहसा फॉर्ममध्ये लिहितो

जिथे div A हे वेक्टर A च्या क्षेत्राचे विचलन आहे,

सीमाच्या पृष्ठभागाच्या बाह्य सामान्य n च्या युनिट वेक्टरद्वारे वेक्टर A चे स्केलर उत्पादन आहे; गणिती साहित्यात हे पूर्वी गॉस आणि ग्रीनच्या नावांशी संबंधित होते.

खरं तर, स्फेरॉईड्सच्या आकर्षणावरील गॉसच्या कामात, एखादी व्यक्ती फक्त सूत्र (1) ची विशेष उदाहरणे पाहू शकते, उदाहरणार्थ, जे = ग्रीन साठी, त्याच्या कामात विजेच्या सिद्धांतावर आणि सूत्र (1) चे चुंबकत्व अजिबात नाही; यामुळे तिहेरी आणि दुहेरी समाकलनांमधील आणखी एक संबंध प्राप्त झाला, म्हणजे, लॅप्लेस ऑपरेटरसाठी ग्रीनचे सूत्र, जे फॉर्ममध्ये लिहिले जाऊ शकते

अर्थात, सेट करून सूत्र (1) (2) वरून काढणे शक्य आहे

आणि त्याच प्रकारे तुम्ही सूत्र (1) पासून सूत्र (2) मिळवू शकता, परंतु ग्रीनने हे करण्याचा विचारही केला नाही.

जिथे व्हॉल्यूमवरील इंटीग्रल डावीकडे आहे आणि सीमेच्या पृष्ठभागावरील इंटीग्रल उजवीकडे आहे आणि हे बाह्य सामान्यचे दिशा कोसाइन आहेत.

ऑस्ट्रोग्राडस्कीच्या पॅरिसियन हस्तलिखिते पूर्ण खात्रीने साक्ष देतात की अविभाज्य प्रमेय (1) चा शोध आणि पहिला संवाद दोन्ही त्याच्या मालकीचे होते. 13 फेब्रुवारी 1826 रोजी पॅरिस अ‍ॅकॅडमी ऑफ सायन्सेसला सादर केलेल्या "अविभाज्य कॅल्क्युलसच्या प्रमेयाचा पुरावा" मध्ये तो पहिल्यांदाच व्यक्त आणि सिद्ध झाला, त्यानंतर तो पुन्हा त्या भागात तयार करण्यात आला. “आतल्या उष्णतेच्या प्रसारावर संस्मरण घन”, जे ऑस्ट्रोग्राडस्कीने 6 ऑगस्ट, 1827 रोजी सादर केले.“ स्मरणिका ”फूरियर आणि पॉइसनला पुनरावलोकनासाठी देण्यात आली होती आणि नंतरच्याने ते नक्कीच वाचले, हे हस्तलिखिताच्या दोन्ही भागांच्या पहिल्या पानांच्या नोंदीवरून दिसून येते. अर्थात, पॉइसनने स्वत: ला प्रमेय ठरवण्याचा विचारही केला नाही, जो त्याला लवचिकतेच्या सिद्धांतावरील त्याच्या कार्याच्या सादरीकरणाच्या दोन वर्षांपूर्वी ऑस्ट्रोग्राडस्कीच्या कामात भेटला.

ऑस्ट्रोग्राडस्की आणि ग्रीनच्या अनेक अविभाज्य गोष्टींमधील संबंधांबद्दल, आम्हाला आठवते की "नोट ऑफ द थ्योरी ऑफ हीट" मध्ये एक सूत्र काढण्यात आले होते जे ग्रीनचे स्वतःचे सूत्र स्वीकारते, एक विशेष बाब म्हणून. ऑस्ट्रोग्राडस्कीने "टीप" मध्ये वापरलेल्या कॉचीचे आताचे असामान्य प्रतीकवाद, अलीकडे पर्यंत संशोधकांनी हा महत्त्वाचा शोध लपविला होता. अर्थात, ग्रीनने शोध आणि सन्मान 1828 मध्ये लॅप्लेस ऑपरेटर्ससाठी त्याच्या नावाच्या सूत्राचे पहिले प्रकाशन राखले आहे.

ट्रिपल इंटिग्रलचे दुहेरी इंटिग्रल मध्ये रुपांतर करण्याच्या सूत्राच्या शोधाने ऑस्ट्रोग्राडस्कीला एन-फोल्ड इंटिग्रल बदलण्याची समस्या सोडवण्यास मदत केली, म्हणजे, विचलनाच्या प्रकाराच्या अभिव्यक्तीच्या अविभाज्य परिवर्तनासाठी सामान्य सूत्र प्राप्त करण्यासाठी एन-डायमेन्शनल डोमेनवर आणि L (x, y, z, ...) = 0 समीकरणासह बाउंडिंग सुपर-सरफेस S वर अविभाज्य. जर आपण मागील नोटेशनचे पालन केले तर सूत्राला फॉर्म आहे

तथापि, ऑस्ट्रोग्राडस्कीने आम्ही वापरलेल्या भौमितिक प्रतिमा आणि अटी वापरल्या नाहीत: बहुआयामी जागांची भूमिती त्या वेळी अद्याप अस्तित्वात नव्हती.

मल्टीपल इंटिग्रल्सच्या भिन्नतेच्या कॅल्क्युलसवरील संस्मरणात, अशा समाकलनाच्या सिद्धांताचे आणखी दोन महत्त्वाचे प्रश्न विचारात घेतले आहेत. प्रथम, ऑस्ट्रोग्राडस्की बहु -आयामी अभिन्न मध्ये चल बदलण्यासाठी एक सूत्र वजा करते; दुसरे, प्रथमच तो योग्य मर्यादेत प्रत्येक व्हेरिएबल्सवर n सलग एकत्रीकरणाचा वापर करून एन-फोल्ड इंटिग्रलची गणना करण्याच्या पद्धतीचे संपूर्ण आणि अचूक वर्णन देतो. शेवटी, या संस्मरणात समाविष्ट असलेल्या सूत्रांमधून, ते काढणे सोपे आहे सामान्य नियमबहुआयामी इंटिग्रलच्या पॅरामीटरच्या संदर्भात भेदभाव, जेव्हा केवळ एकात्मिकच नाही तर एकत्रीकरणाच्या क्षेत्राची सीमा देखील या पॅरामीटरवर अवलंबून असते. हा नियम संस्मरणात उपस्थित असलेल्या सूत्रांनुसार अशा नैसर्गिक मार्गाने पुढे आला आहे की नंतरच्या गणितज्ञांनी या संस्मरणातील सूत्रांपैकी एकासह ते ओळखले.

ऑस्ट्रोग्राडस्कीने एकाधिक इंटीग्रलमध्ये व्हेरिएबल्स बदलण्यासाठी एक विशेष कार्य केले. दुहेरी समाकलनासाठी, संबंधित नियम युलरद्वारे औपचारिक परिवर्तन वापरून, तिप्पट अविभाज्य, लाग्रेंजद्वारे वापरण्यात आला. तथापि, लाग्रेंजचा निकाल योग्य असला तरी, त्याचा तर्क अचूक नव्हता: तो जुन्या आणि नवीन चलनातील खंड घटक - निर्देशांक - एकमेकांच्या समान आहेत या वस्तुस्थितीवरून पुढे जात असल्याचे दिसत होते. ऑस्ट्रोग्राडस्कीने चल बदलण्यासाठी नियमाच्या फक्त नमूद केलेल्या व्युत्पत्तीमध्ये अशीच चूक केली. "एकाधिक इंटिग्रलमध्ये व्हेरिएबल्सच्या परिवर्तनावर" या लेखात, ऑस्ट्रोग्राडस्कीने लाग्रेंजची त्रुटी उघड केली आणि प्रथमच व्हेरिएबल्सला दुहेरी इंटिग्रलमध्ये बदलण्यासाठी स्पष्ट भौमितिक पद्धत सादर केली, जी थोड्या अधिक कठोर स्वरूपात देखील सादर केली गेली. आमच्या नियमावली. म्हणजे, सूत्रांद्वारे इंटिग्रलमधील व्हेरिएबल्स बदलताना, एकीकरणाचे क्षेत्र u = const, v = const या दोन प्रणालींच्या समन्वय रेषांद्वारे विभाजित केले जाते. नंतर अविभाज्य संकीर्ण वक्ररेषेच्या पट्टीशी संबंधित असणाऱ्या घटकांमध्ये आधी जोडून, आणि नंतर, सर्व घटक संपत नाहीत तोपर्यंत पट्ट्यांद्वारे घटकांची बेरीज करून अविभाज्य मिळवता येते. एक साधी गणना एका क्षेत्रासाठी देते जी लहान उच्च क्रम पर्यंत समांतरभुज म्हणून मानली जाऊ शकते, अभिव्यक्ती, जिथे, निवडली जाते जेणेकरून क्षेत्र सकारात्मक असेल. परिणामी, आम्हाला सुप्रसिद्ध सूत्र मिळते

म्हणून परिभाषित केलेल्या दोन व्हेरिएबल्सच्या कार्यासाठी z = f(x, y) .

दुहेरी अविभाज्य असे लिहिले आहे:

येथे डी- रेषांनी बांधलेला एक सपाट आकृती, ज्याचे अभिव्यक्ती (समानता) दुहेरी समाकलनाची गणना करण्याच्या कामात दिली जातात. डावे आणि उजवे - समानता ज्यामध्ये डावीकडील व्हेरिएबल x, आणि वर आणि खाली - समानता ज्यात डावीकडील व्हेरिएबल आहे y... हे ठिकाण आणि पुढे - दुहेरी अविभाज्य गणना करण्याचे तंत्र समजून घेण्यासाठी सर्वात महत्वाचे.

दुहेरी अभिन्न गणना करा - म्हणजे नमूद केलेल्या आकृतीच्या क्षेत्रफळाएवढी संख्या शोधणे डी .

आम्ही स्पर्श करेपर्यंत दुहेरी अभिन्न व्याख्या , पण आम्ही त्याची गणना करायला शिकू. दुहेरी अविभाज्य म्हणजे काय हे समजणे सोपे आहे जेव्हा आपण त्याची गणना करण्यासाठी अनेक समस्या सोडवल्या आहेत, म्हणून आपल्याला या धड्याच्या शेवटी दुहेरी समाकलनाची व्याख्या मिळेल. थोडे पुढे धावताना, आम्ही फक्त लक्षात घेऊ शकतो की दुहेरी अभिन्न ची व्याख्या देखील वर नमूद केलेल्या आकृतीशी संबंधित आहे डी .

जर आकृती डीएक आयत आहे, त्याला जोडणाऱ्या सर्व रेषा सरळ रेषा आहेत. जर आकृती डी- वक्ररेखा आहे, नंतर डावीकडे आणि उजवीकडे ती सरळ रेषांनी, आणि वर आणि खाली - असाइनमेंटमध्ये दिलेल्या समानतेद्वारे दिलेल्या वक्र रेषांनी बांधलेली आहे. काही वेळा आहेत जेव्हा आकृती डी- एक त्रिकोण, परंतु अशा प्रकरणांबद्दल थोडे पुढे.

दुहेरी अविभाज्य गणना करण्यासाठी, म्हणून, आकृतीला जोडलेल्या रेषांची क्रमवारी करणे आवश्यक आहे डी, ज्याचे कडक नाव आहे - एकीकरणाचे क्षेत्र. डावीकडे आणि उजवीकडे आणि वर आणि खाली क्रमवारी लावा. हे तेव्हा आवश्यक असेल पुनरावृत्ती अभिन्न करण्यासाठी दुहेरी अविभाज्य कमी करणे - दुहेरी अभिन्न गणना करण्याची पद्धत.

आयताकृती क्षेत्र प्रकरण:

वक्र प्रदेश प्रकरण:

आणि हे आधीच आम्हाला परिचित असलेल्या काही समाकलनाचे समाधान आहे, ज्यामध्ये एकत्रीकरणाच्या वरच्या आणि खालच्या मर्यादा दिल्या आहेत. अभिव्यक्ती जे आकार बांधणाऱ्या रेषा परिभाषित करतात डी, सामान्य निश्चित समाकलनासाठी एकात्मतेची मर्यादा असेल, ज्याकडे आपण आधीच येत आहोत.

दुहेरी इंटिग्रलची पुनरावृत्ती इंटिग्रल कमी करणे

आयताकृती क्षेत्र केस

अशा फंक्शनला डबल इंटिग्रल असू द्या

ला या दुहेरी समाकलनाची गणना करा , तो एक पुनरावृत्ती अभिन्न करण्यासाठी कमी करणे आवश्यक आहे, ज्याचे स्वरूप आहे

प्रथम आपल्याला आतील (उजवे) निश्चित अविभाज्य, नंतर - बाह्य (डावे) निश्चित अभिन्न गणना करणे आवश्यक आहे.

आपण भूमिका बदलू शकता xआणि y

उदाहरण 1.दुहेरी अभिन्न गणना करा

Y हे स्थिर आहे असे गृहीत धरून आम्ही आतील (उजवे) अविभाज्य गणना करतो. आम्ही प्राप्त करतो.

उदाहरण 2.दुहेरी अभिन्न गणना करा

उपाय. हे दुहेरी इंटिग्रल पुनरावृत्ती इंटीग्रलमध्ये कमी करा

रेखांकनात, आम्ही एकत्रीकरणाचे क्षेत्र तयार करतो:

आता आम्ही फक्त गणना केलेल्या आतील (उजव्या) समाकलनाच्या बाह्य (डाव्या) समाकलनाची गणना करतो:

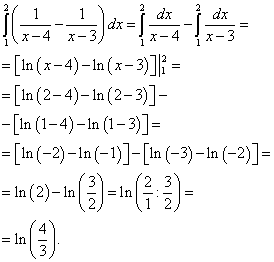
परिणाम या दुहेरी समाकलनाचा उपाय असेल.

दुहेरी अविभाज्य स्वतःची गणना करा आणि नंतर उपाय पहा

वक्र किंवा त्रिकोणी प्रदेशाचे प्रकरण

पुन्हा दोन व्हेरिएबल्सचे फंक्शन दिले जाऊ द्या f(x, y) , आणि साठी निर्बंध डी: आधीच थोड्या वेगळ्या प्रकारची:

ही नोंद म्हणजे आकृती डीडाव्या आणि उजव्या बाजूस, जसे रेक्टिलाइनर प्रदेशाच्या बाबतीत - सरळ रेषा x = अआणि x = ब, परंतु खाली आणि वर वक्र आहेत जे समीकरणांनी दिले आहेत आणि. दुसऱ्या शब्दांत, आणि कार्ये आहेत.

अशा फंक्शनला देखील डबल इंटिग्रल असू द्या

या दुहेरी समाकलनाची गणना करण्यासाठी, ते पुनरावृत्ती केलेल्या अविभाज्य मध्ये कमी करणे आवश्यक आहे, ज्याचे स्वरूप आहे

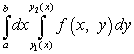येथे एकीकरणाच्या मर्यादा अआणि बसंख्या आहेत, आणि कार्ये आहेत. त्रिकोणी प्रदेशाच्या बाबतीत, फंक्शन्सपैकी एक किंवा सरळ रेषेचे समीकरण आहे. उदाहरण 3 मध्ये या प्रकरणाचे विश्लेषण केले जाईल.

रेक्टिलाइनर प्रदेशाच्या बाबतीत, आपल्याला प्रथम योग्य निश्चित अभिन्न, नंतर डावे निश्चित अविभाज्य गणना करणे आवश्यक आहे.

त्याचप्रमाणे, तुम्ही भूमिका बदलू शकता xआणि y... मग पुनरावृत्त इंटिग्रलला फॉर्म असेल

अशा वारंवार समाकलनाचे निराकरण त्याच प्रकारे केले पाहिजे: प्रथम, आतील (उजवे) अविभाज्य, नंतर बाह्य (डावे) अविभाज्य.

उदाहरण 5.दुहेरी अभिन्न गणना करा

उपाय. हे दुहेरी इंटिग्रल पुनरावृत्ती इंटीग्रलमध्ये कमी करा

रेखांकनात, आम्ही एकत्रीकरण क्षेत्र तयार करतो आणि ते त्रिकोणी आहे हे पाहू:

X ची स्थिरता लक्षात घेऊन आम्ही आतील (उजवीकडे) अविभाज्य गणना करतो. आम्ही प्राप्त करतो.

आता आम्ही फक्त गणना केलेल्या आतील (उजव्या) समाकलनाच्या बाह्य (डाव्या) समाकलनाची गणना करतो. प्रथम, आम्ही हे अविभाज्य समाकलनाची बेरीज म्हणून दर्शवतो:

आम्ही पहिल्या टर्मची गणना करतो:

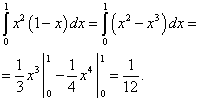
आम्ही दुसऱ्या टर्मची गणना करतो:

आम्ही तिसऱ्या टर्मची गणना करतो:

आम्हाला बेरीज मिळते, जे या दुहेरी समाकलनाचे समाधान असेल:

उदाहरण 6.दुहेरी अभिन्न गणना करा

उपाय. हे दुहेरी इंटिग्रल पुनरावृत्ती इंटीग्रलमध्ये कमी करा

रेखांकनात, आम्ही एकत्रीकरणाचे क्षेत्र तयार करतो:

परिणाम या दुहेरी समाकलनाचा उपाय असेल.

x- बरोबर आणि अयोग्य, y- एकत्रीकरणाचे योग्य आणि चुकीचे डोमेन

असे घडते की दुहेरी इंटिग्रलच्या समाकलनाचा प्रदेश अशा रेषांनी बांधलेला असतो की एकत्रीकरणाच्या प्रदेशाला भागांमध्ये विभाजित करणे आणि प्रत्येक संबंधित पुनरावृत्ती केलेले अविभाज्य स्वतंत्रपणे सोडवणे आवश्यक होते. ही प्रकरणे आहेत जेव्हा:

1) एकत्रीकरणाचे क्षेत्र कमी किंवा वरच्या (डाव्या किंवा उजव्या) सीमेच्या स्वरूपात दोन किंवा अधिक सरळ किंवा वक्र रेषा असलेली आकृती आहे;

2) एकत्रीकरणाचा प्रदेश हा एक आकृती आहे, ज्याच्या सरळ रेषा दोन पेक्षा जास्त बिंदूंना छेदतात.

वरील एकत्रीकरणाच्या प्रदेशाच्या डाव्या किंवा उजव्या सीमेवर लागू झाल्यास, म्हणजे, व्यक्त केलेल्या रेषांद्वारे निर्धारित मर्यादा x, नंतर एकत्रीकरणाचा प्रदेश म्हणतात x-चुकीचे. जर सरळ y = y0 केवळ एकाच बिंदूवर संबंधित सीमेला छेदते आणि जर फक्त एक सरळ रेषा किंवा वक्र सीमा म्हणून काम करते, तर एकत्रीकरणाच्या क्षेत्राला म्हणतात x- योग्य

त्याचप्रमाणे, जर व्यक्त केलेल्या रेषांद्वारे परिभाषित केलेली सीमा y, सरळ x = x0 एकापेक्षा जास्त बिंदूंना छेदतात किंवा जर एकापेक्षा जास्त सरळ रेषा किंवा वक्र सीमा म्हणून काम करतात तर एकत्रीकरणाच्या क्षेत्राला म्हणतात y-चुकीचे. आता चिन्हे दाखवा y-योग्य क्षेत्र, बहुधा, अगदी सोपे आहे.

आतापर्यंत, आम्ही उदाहरणे बघितली आहेत x- चुकीचे आणि y-समाकलनाची योग्य क्षेत्रे. आता जेव्हा शुद्धतेच्या अटीचे उल्लंघन केले जाते तेव्हा प्रकरणांचा विचार करूया.

उदाहरण 7.दुहेरी अविभाज्य गणना करा, ज्याचे एकत्रीकरण क्षेत्र ओळींनी बांधलेले आहे y = x , xy = 1 , y = 2 .

उपाय. एकत्रीकरणाचे क्षेत्र आहे yचुकीचे, कारण त्याची खालची सीमा एका ओळीने सेट केली जाऊ शकत नाही y = y(x) ... जसे तुम्ही वरील चित्रात पाहू शकता, खालची सीमा बनलेली आहे y = x(गडद बरगंडी) आणि xy= 1 (हिरवा). म्हणून थेट x= 1 (काळा) आम्ही एकत्रीकरणाचे क्षेत्र दोन भागांमध्ये विभागू शकतो - आणि.

हे दुहेरी अविभाज्य खालीलप्रमाणे मोजले जाते:

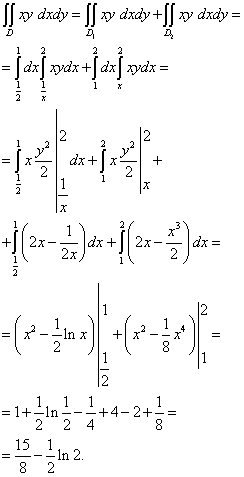
एकत्रीकरणाचा क्रम बदलणे

वर नमूद केल्याप्रमाणे, पुनरावृत्ती केलेल्या इंटिग्रलमध्ये दुहेरी इंटिग्रल कमी केल्यानंतर, व्हेरिएबल्स बदलू शकतात xआणि yभूमिका, किंवा, दुसऱ्या शब्दांत, एकत्रीकरणाचा क्रम बदला.

एकत्रीकरणाच्या क्रमातील बदलाचे "हेन्रीबद्दल" खालील शब्दांद्वारे लाक्षणिक वर्णन केले जाऊ शकते: जंगलवासी असे कसे वागतो - एक पशू, एकदा पिंजऱ्यात, आणि पिंजरामध्ये राहणारा असाच वागतो - एक माणूस, हरवलेला शंकांचे जंगल. "आणि तेच:" चाल्मर्सने ते पत्र हजारो लहान तुकड्यांमध्ये फाडले आणि त्याच्या महागड्या गालिचे फाडायला सुरुवात केली, त्यावर मागे पुढे सरकत होते. " ( हेन्री. मॅडिसन स्क्वेअरचे शेहेराझाडे.)

मग, जर आपल्याकडे व्हेरिएबलच्या संदर्भात डावा अविभाज्य असेल x, आणि योग्य एक - द्वारे y, नंतर एकीकरणाचा क्रम बदलल्यानंतर सर्व काही उलट होईल. मग "नवीन" गेमसाठी एकत्रीकरणाच्या मर्यादा "जुन्या" x कडून "उधार" घेतल्या पाहिजेत आणि "नवीन" x साठी एकत्रीकरणाच्या मर्यादा फॉर्ममध्ये मिळाल्या पाहिजेत व्यस्त कार्य, x साठी समीकरण सोडवून, ज्याने गेमची मर्यादा निश्चित केली.

उदाहरण 8.

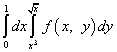उपाय. समाकलनाचा क्रम बदलल्यानंतर, गेमवरील इंटीग्रल डावे होते आणि एक्स वर इंटिग्रल उजवे होते. "नवीन" गेमसाठी एकत्रीकरणाच्या मर्यादा "जुन्या" x कडून घेतल्या जातील, म्हणजेच, खालची मर्यादा शून्याच्या बरोबरीची असेल आणि वरची मर्यादा एकाच्या समान असेल. "जुन्या" गेमसाठी एकात्मतेच्या मर्यादा समीकरणांद्वारे दिल्या जातात आणि. X साठी ही समीकरणे सोडवल्यानंतर, आम्हाला x साठी समाकलनाच्या नवीन मर्यादा मिळतात:

(तळाशी) आणि (वर).

अशा प्रकारे, एकत्रीकरणाचा क्रम बदलल्यानंतर, पुनरावृत्ती समाकलित खालीलप्रमाणे लिहिले जाईल:

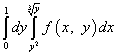दुहेरी इंटिग्रलमध्ये एकत्रीकरणाचा क्रम बदलल्यानंतर, एकत्रीकरण क्षेत्र अनेकदा बदलते y-चुकीचे किंवा x- चुकीचा (मागील परिच्छेद पहा). मग एकत्रीकरणाचे क्षेत्र भागांमध्ये विभाजित करणे आणि प्रत्येक संबंधित पुनरावृत्ती अविभाज्य स्वतंत्रपणे सोडवणे आवश्यक आहे.

एकीकरण क्षेत्राला भागांमध्ये विभाजित केल्यामुळे अनेक विद्यार्थ्यांसाठी काही अडचणी येतात, आम्ही मागील परिच्छेदात दिलेल्या उदाहरणापर्यंत स्वतःला मर्यादित ठेवणार नाही, परंतु आणखी काही उदाहरणे विचारात घेऊ.

उदाहरण 9.पुन्हा समाकलनासाठी एकत्रीकरणाचा क्रम बदला

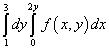उपाय. तर, या पुनरावृत्ती केलेल्या समाकलनाचे क्षेत्र सरळ रेषांनी बांधलेले आहे y = 1 , y = 3 , x = 0 , x = 2y .

वेगळ्या क्रमाने समाकलित करताना, प्रदेशाच्या खालच्या सीमेमध्ये दोन सरळ रेषा असतात: एबीआणि इ.स.पूजे समीकरणांद्वारे दिले जातात y= 1 आणि y = x/ 2, जे खालील आकृतीमध्ये पाहिले जाऊ शकते.

या अनिश्चिततेतून बाहेर पडण्याचा मार्ग म्हणजे एकीकरण क्षेत्राचे दोन भाग करणे. एकत्रीकरण क्षेत्र सरळ रेषेने विभागले जाईल बीएम... व्यस्त कार्य शोधून आम्ही एकत्रीकरणाच्या नवीन मर्यादांची गणना करतो. या समाधानाच्या अनुसार, समाकलनाचा क्रम बदलल्यानंतर पुनरावृत्ती अभिन्न दोन समाकलांच्या बेरजेइतकी असेल:

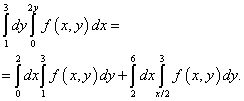
स्वाभाविकच, दुहेरी समाकलनाचे तेच समाधान असेल, जे या उदाहरणाच्या स्थितीत दिलेल्या पुनरावृत्ती समाकलनापर्यंत कमी होते.

उदाहरण 10.पुन्हा समाकलनासाठी एकत्रीकरणाचा क्रम बदला

उपाय. तर, पुनरावृत्ती केलेल्या समाकलनाचे क्षेत्र सरळ रेषांनी बांधलेले आहे x = 0 , x= 2 आणि वक्र आणि.

खालील चित्रात पाहिल्याप्रमाणे, अक्षांशी समांतर एक सरळ रेषा 0x, दोन पेक्षा जास्त बिंदूंवर एकत्रीकरण क्षेत्राची खालची सीमा ओलांडेल.

म्हणून, आम्ही एकत्रीकरणाचा प्रदेश सरळ रेषांनी तीन भागांमध्ये विभागू, जे आकृतीमध्ये काळ्या रंगात काढले आहेत. व्यस्त कार्य शोधून आम्ही एकत्रीकरणाच्या नवीन मर्यादांची गणना करतो. एकत्रीकरणाच्या तीन नवीन क्षेत्रांची मर्यादा खालीलप्रमाणे असेल.

या सोल्यूशननुसार, इंटिग्रेशनचा क्रम बदलल्यानंतर पुनरावृत्त इंटिग्रल तीन इंटिग्रल्सच्या बेरीजच्या समान असेल:

तीन इंटीग्रल्सची समान बेरीज दुहेरी इंटिग्रलच्या बरोबरीची असेल, जी या उदाहरणाच्या स्थितीत दिलेल्या पुनरावृत्ती इंटिग्रलमध्ये कमी होते.

आणि तरीही, जबरदस्तीची परिस्थिती बऱ्याचदा आधीच्या पायरीवर असलेल्या विद्यार्थ्यांमध्ये हस्तक्षेप करते - एकात्मतेची मर्यादा ठरवते. चिंता आणि गोंधळ काही कारणाशिवाय नाही: जर एकत्रीकरण क्षेत्राला भागांमध्ये विभागण्यासाठी, आणि वारंवार समाकलित केलेले - समाकलनाचे सारण सोडवण्यासाठी रेखांकनाकडे पाहणे पुरेसे असेल तर, एकीकरण मर्यादा निश्चित करण्यासाठी काही प्रशिक्षण अनुभव आवश्यक आहे . चला आपण एका उदाहरणाद्वारे चालवूया ज्यात आपण केवळ एकीकरणाच्या मर्यादांच्या व्यवस्थेवर आणि जवळजवळ स्वयंचलितपणे डोमेनच्या विभाजनावर लक्ष केंद्रित करू आणि सोल्यूशन स्वतःच वगळू.

उदाहरण 11.एकत्रीकरणाचा प्रदेश असल्यास दुहेरी समाकलनाच्या मर्यादा शोधा डीखालीलप्रमाणे सेट केले आहे:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

उपाय. स्पष्टपणे (माध्यमातून xआणि y"अशुद्धीशिवाय"), एकत्रीकरणाच्या क्षेत्राशी जोडलेल्या रेषा निर्दिष्ट नाहीत. X साठी असल्याने, ते बहुतेक वेळा गेमद्वारे व्यक्त केलेल्या वरच्या आणि खालच्या सीमेला स्पर्श करणाऱ्या सरळ रेषा बनतात, मग आपण या मार्गावर नक्की जाऊ. शिवाय, एकत्रीकरणाचा क्रम बदलताना, आम्हाला समान क्षेत्रासह एकत्रीकरण प्रदेश मिळतो. चला खेळाच्या संदर्भात असमानता सोडवू आणि मिळवू:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

आम्ही रेखांकनात परिणामी ओळी तयार करतो. X- एकत्रीकरण मर्यादा खरंच रेषा आहेत x= 0 आणि x= 2. पण एकीकरणाचे क्षेत्र निघाले yचुकीचे, कारण त्याची वरची सीमा एका ओळीने सेट केली जाऊ शकत नाही y = y(x) .

Depositfiles वरून डाउनलोड करा

व्याख्याने 5-6

विषय 2. एकाधिक अभिन्न.

दुहेरी अभिन्न.

प्रश्न नियंत्रित करा.

1. दुहेरी अभिन्न, त्याचा भौमितिक आणि भौतिक अर्थ

2. दुहेरी समाकलनाचे गुणधर्म.

3. कार्टेशियन निर्देशांकांमध्ये दुहेरी समाकलनाची गणना.

4. व्हेरिएबल्सचा दुहेरी इंटिग्रलमध्ये बदल. ध्रुवीय निर्देशांकांमध्ये दुहेरी समाकलनाची गणना.

कार्य करू द्या z = f (x , y) मर्यादित बंद प्रदेशात परिभाषित केले आहे डीविमान क्षेत्र विघटन करू डीअनियंत्रितपणे चालू nप्राथमिक बंद प्रदेश  1 , … , nक्षेत्रांसह  1 , …,   nआणि व्यास d 1 , …, d n अनुक्रमे. आम्ही दर्शवतो dप्रदेशांचा सर्वात मोठा व्यास  1 , … ,  n... प्रत्येक क्षेत्रात  केएक अनियंत्रित बिंदू निवडा पी के (x के , y के) आणि लिहा अविभाज्य बेरीजकार्य f(x, y)

एस =
(1)

व्याख्या. दुहेरी अभिन्नकार्य f(x, y) क्षेत्रानुसार डीअविभाज्य रकमेची मर्यादा म्हणतात

, (2)

जर ते अस्तित्वात असेल.

टिप्पणी. अविभाज्य बेरीज एसप्रदेशाचे विभाजन कसे होते यावर अवलंबून आहे डीआणि बिंदू निवड पी के (के=1, …, n). मात्र, मर्यादा
, जर ते अस्तित्वात असेल, तर प्रदेश विभाजन करण्याच्या पद्धतीवर अवलंबून नाही डीआणि बिंदू निवड पी के .

दुहेरी अविभाज्य अस्तित्वासाठी पुरेशी अट. फंक्शन असल्यास डबल इंटिग्रल (1) अस्तित्वात आहे f(x, y) मध्ये सतत डीतुकडावार गुळगुळीत वक्र मर्यादित संख्या वगळता आणि मध्ये बांधलेले आहे डी... खालीलप्रमाणे, आम्ही असे गृहीत धरू की विचाराधीन सर्व दुहेरी अभिन्न घटक अस्तित्वात आहेत.

दुहेरी समाकलनाचा भौमितीय अर्थ.

तर f(x, y) परिसरात ≥0 डी, नंतर दुहेरी अविभाज्य (1) आकृतीमध्ये दर्शविलेल्या "दंडगोलाकार" शरीराच्या परिमाणांइतके आहे:

व्ही =
(3)

एक दंडगोलाकार शरीर खाली एका क्षेत्राने बांधलेले आहे डी, पृष्ठभागाच्या वरच्या भागापासून z = f (x , y), बाजूंवर - या पृष्ठभागाच्या आणि प्रदेशाच्या सीमांना जोडणाऱ्या उभ्या रेषा विभागांद्वारे डी.

दुहेरी अभिन्न चा भौतिक अर्थ. सपाट प्लेट वस्तुमान.

एक सपाट प्लेट द्या डीज्ञात घनता कार्यासह γ ( एनएस,येथे), नंतर प्लेट D चे भाग D मध्ये विभाजित करणे मीआणि अनियंत्रित गुण निवडणे
, आम्ही प्लेट माससाठी मिळवतो
, किंवा, सूत्राशी तुलना (2):

(4)

4. दुहेरी समाकलनाचे काही गुणधर्म.

रेषीयता.तर सोबतएक अंकीय स्थिरांक आहे, तर

अॅडिटिव्हिटी.जर क्षेत्र डी क्षेत्रांमध्ये "विभाजित" डी 1 आणि डी 2, नंतर

3) मर्यादित क्षेत्राचे क्षेत्र डीच्या समान आहे

(5)

कार्टेशियन निर्देशांकांमध्ये दुहेरी समाकलनाची गणना.

प्रदेश द्या

चित्र 1

डी = { (x , y ): a ≤ x ≤ b , φ 1 (x ) ≤ y≤ 2 (x ) } (6)

प्रदेश डी सरळ रेषांमधील पट्टीमध्ये बंद x = अ , y = ब, खाली आणि वरून अनुक्रमे वक्रांनी बांधलेले आहे y = φ 1 (x ) आणि y = φ 2 (x ) .

क्षेत्रावर दुहेरी अभिन्न (1) डी(4) पुनरावृत्ती केलेल्या अविभाज्य भागातून गणना केली जाते:

(7)

हे पुनरावृत्ती अभिन्न खालीलप्रमाणे मोजले जाते. प्रथम, अंतर्गत अभिन्न गणना केली जाते

व्हेरिएबल द्वारे y, ज्यात xस्थिर मानले जाते. परिणाम व्हेरिएबलचे कार्य आहे x, आणि नंतर व्हेरिएबलच्या संदर्भात या कार्याचे "बाह्य" अविभाज्य गणना केली जाते x .

टिप्पणी. फॉर्म्युला (7) नुसार पुनरावृत्ती केलेल्या समाकलनाकडे जाण्याच्या प्रक्रियेस बऱ्याचदा दुहेरी अभिन्न मध्ये एकात्मतेच्या मर्यादांची व्यवस्था म्हणतात. एकीकरणाच्या मर्यादा ठरवताना दोन मुद्दे लक्षात ठेवले पाहिजेत. प्रथम, समाकलनाची खालची मर्यादा वरच्या एकापेक्षा जास्त नसावी; दुसरे म्हणजे, बाह्य समाकलनाच्या मर्यादा स्थिर असाव्यात, आणि आंतरिक समाकलन सामान्यतः बाह्य समाकलनाच्या समाकलनाच्या परिवर्तनावर अवलंबून असावे.

आता प्रदेश द्या डीफॉर्म आहे

डी = { (x , y ) : c ≤ y ≤ d , ψ 1 (y ) ≤ x ≤ 2 (y ) } . (8)

मग

. (9)

समजा ते क्षेत्र डीएकाच वेळी (6) आणि (8) स्वरूपात दर्शविले जाऊ शकते. मग समानता

(10)

समानतेच्या (10) एका पुनरावृत्तीपासून दुसर्यापर्यंतच्या परिच्छेदाला म्हणतात एकत्रीकरणाचा क्रम बदलणेदुहेरी अभिन्न मध्ये.

उदाहरणे.

1) इंटिग्रल मध्ये एकत्रीकरणाचा क्रम बदला

उपाय. पुनरावृत्त अभिन्न स्वरूपापासून, आम्हाला प्रदेश सापडतो

डी = { (x , y ): 0 ≤ x 1, 2 x ≤ y≤ 2 } .

क्षेत्र काढू डी... आकृतीवरून, आपण पाहतो की हे क्षेत्र सरळ रेषांमधील आडव्या पट्टीमध्ये स्थित आहे y =0, y= 2 आणि रेषा दरम्यान x =0 आणि x= डी

कधीकधी गणना सुलभ करण्यासाठी व्हेरिएबल्स बदलल्या जातात:

,
(11)

जर कार्ये (11) सतत भिन्न असतात आणि निर्धारक (जेकबियन) विचारात घेतलेल्या डोमेनमध्ये शून्य आहेत:

(12)

रशियन फेडरेशनचे शिक्षण आणि विज्ञान मंत्रालय

अभ्यासक्रमाचे काम

शिस्त: उच्च गणित

(बेसिक लिनियर प्रोग्रामिंग)

विषयावर: अनेक एकात्मिक

पूर्ण: ______________

शिक्षक: ___________

तारीख ___________________

ग्रेड _________________

स्वाक्षरी ________________

वोरोनेझ 2008

1 एकाधिक समाकलित

1.1 दुहेरी अभिन्न

1.2 तिप्पट अविभाज्य

1.3 वक्ररेखा समन्वय मध्ये अनेक समाकलित

1.4 एकाधिक समाकलनाचे भौमितिक आणि भौतिक अनुप्रयोग

2 वक्र आणि पृष्ठभाग समाकलित

2.1 वक्ररेखा समाकलित

2.2 पृष्ठभाग समाकलित

2.3 भौमितिक आणि भौतिक अनुप्रयोग

ग्रंथसूची

1 एकाधिक समाकलित

1.1 दुहेरी अभिन्न

ऑक्सी प्लेनमध्ये बंद रेषा D चा रेषा L ने बांधलेला विचार करा. आम्ही हा प्रदेश काही ओळींनी n भागांमध्ये विभागतो

, आणि या प्रत्येक भागातील बिंदूंमधील संबंधित सर्वात मोठे अंतर d 1, d 2, ..., d n द्वारे दर्शविले जाईल. चला प्रत्येक भागात बिंदू Р i निवडा.

फंक्शन z = f (x, y) D डोमेनमध्ये दिले जाऊ द्या. आपण f (P 1), f (P 2),…, f (P n) द्वारे दर्शवू या निवडलेल्या बिंदूंवर या फंक्शनची मूल्ये आणि f (P i) --S i फॉर्मच्या उत्पादनांची बेरीज तयार करा. :

, (1)

डोमेन D मध्ये f (x, y) फंक्शनसाठी अभिन्न बेरीज म्हणतात.

जर अविभाज्य रकमेची समान मर्यादा (1) अस्तित्वात असेल

आणि, जे एकतर D डोमेनचे भागांमध्ये विभाजन करण्याच्या पद्धतीवर अवलंबून नाही, किंवा त्यामध्ये P i च्या बिंदूंच्या निवडीवर अवलंबून नाही, तर त्याला डोमेन D वर फ (x, y) फंक्शनचे दुहेरी अविभाज्य म्हटले जाते दर्शविले जाते

. (2)

रेषांनी बांधलेल्या क्षेत्र D वरील दुहेरी समाकलनाची गणना

x = a, x = b (a< b), где φ 1 (х) и φ 2 (х) непрерывны на (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:

(3)

1.2 तिहेरी अविभाज्य

ट्रिपल इंटिग्रलची संकल्पना डबल इंटिग्रलसह सादृश्य द्वारे सादर केली जाते.

काही डोमेन V एका बंद पृष्ठभागाच्या सीमारेषेखालील स्पेसमध्ये दिले जाऊ द्या. या बंद डोमेनमध्ये f (x, y, z) एक सतत फंक्शन परिभाषित करूया. मग आम्ही प्रदेश V ला अनियंत्रित भागांमध्ये विभाजित करतो Δv i, प्रत्येक भागाचे परिमाण Δv i च्या समान असल्याचे गृहीत धरून, आणि फॉर्मची एक अविभाज्य बेरीज तयार करतो

, (4)

येथे मर्यादा

अविभाज्य बेरीज (11), जे डोमेन V च्या विभाजनाच्या पद्धतीवर अवलंबून नाही आणि या डोमेनच्या प्रत्येक उपडोमेनमध्ये P i च्या गुणांची निवड आहे, त्याला f (x, y, z) फंक्शनचे ट्रिपल इंटिग्रल म्हणतात डोमेन V:

. (5)

फ क्षेत्राचे f (x, y, z) V चे त्रिगुण अविभाज्य समान क्षेत्रावरील त्रिगुण अविभाज्य समान आहे:

. (6)

1.3 वक्ररेखा समन्वय मध्ये अनेक समाकलित

चला विमानात वक्ररेखा निर्देशांक सादर करूया, ज्याला ध्रुवीय निर्देशांक म्हणतात. चला बिंदू O (ध्रुव) आणि त्यातून निर्माण होणारा एक किरण (ध्रुवीय अक्ष) निवडूया.

भात. अंजीर 2 3

बिंदू M (Fig. 2) चे निर्देशांक MO विभागाची लांबी असतील - ध्रुवीय त्रिज्या ρ आणि कोन the MO आणि ध्रुवीय अक्ष यांच्या दरम्यान: M (ρ, φ). लक्षात घ्या की विमानाच्या सर्व बिंदूंसाठी, ध्रुव वगळता, ρ> 0, आणि ध्रुवीय कोन positive विरूद्ध दिशेने मोजल्यावर नकारात्मक आणि नकारात्मक दिशेने मोजल्यावर सकारात्मक मानले जाईल.

बिंदू M च्या ध्रुवीय आणि कार्टेशियन निर्देशांकांमधील संबंध ध्रुवीय सह कार्टेशियन समन्वय प्रणालीचे मूळ संरेखित करून आणि सकारात्मक सेमॅक्सिस ऑक्स - ध्रुवीय अक्ष (चित्र 3) सह सेट केले जाऊ शकतात. नंतर x = φcosφ, у = ρsinφ. येथून

, tg.

डोमेन D मध्ये वक्रांनी बांधलेले ρ = Φ 1 (φ) आणि ρ = Φ 2 (φ), जेथे φ 1< φ < φ 2 , непрерывную функцию z = f(φ, ρ) (рис. 4).

(7)

त्रिमितीय जागेत, दंडगोलाकार आणि गोलाकार निर्देशांक प्रविष्ट केले जातात.

बिंदू P (ρ, φ, z) चे दंडगोलाकार निर्देशांक हे ध्रुवीय निर्देशांक आहेत ρ, the या बिंदूच्या प्रक्षेपणाचे विमान ऑक्सी आणि या बिंदूचे अर्ज z (Fig. 5).

अंजीर 5 अंजीर 6

दंडगोलाकार निर्देशांकांपासून कार्टेशियन निर्देशांकांमध्ये संक्रमणाचे सूत्र खालीलप्रमाणे निर्दिष्ट केले जाऊ शकते:

x = φcosφ, y = φsinφ, z = z. (आठ)

गोलाकार निर्देशांकांमध्ये, अंतराळातील एका बिंदूची स्थिती रेषीय समन्वय r द्वारे निर्धारित केली जाते - बिंदूपासून कार्टेशियन समन्वय प्रणालीच्या उत्पत्तीपर्यंतचे अंतर (किंवा गोलाकार प्रणालीचा ध्रुव), φ - सकारात्मक दरम्यान ध्रुवीय कोन सेमॅक्सिस ऑक्स आणि प्लेन ऑक्सीवर बिंदूचा प्रक्षेपण, आणि θ - अक्ष ofz आणि सेगमेंट OP च्या सकारात्मक सेमॅक्सिस दरम्यानचा कोन (चित्र 6). ज्यात

चला गोलाकार निर्देशांकांपासून कार्टेशियन निर्देशांकांमध्ये संक्रमणाची सूत्रे परिभाषित करूया:

x = rsinθcosφ, y = rsinθsinφ, z = rcosθ. (नऊ)

मग ट्रिपल इंटिग्रलमध्ये दंडगोलाकार किंवा गोलाकार निर्देशांकांमध्ये संक्रमणाचे सूत्र असे दिसेल: