Paskaitos daug integralai, dvigubas integralas. Dvigubo integralo skaičiavimas: teorija ir pavyzdžiai Kelių integralų sprendimas

Def . Leisti būti ,
,

.

Rinkinys vadinamas uždaru tarpeliu arba uždaryta juosta .

Rinkinys vadinamas atvira spraga

arba atvirą barą .

Def . Tarpų matavimas ir kiekis vadinamas:

(Tiksliau
).

Def . Jei
toks kad
tada intervalas vadinamas išsigimusiu ir
.

Tarpų matavimo savybės:

a). Teigiamumas:
, ir
Jeigu, ir tik jeigu - yra išsigimęs.

b). Teigiamas vienodumas :.

v). Pridėtumas:

* dėl
toks kad
;

* dėl
ir

.

G). Matavimo monotoniškumas :.

Def . Juostos (tarpo) skersmuo yra vertė:

Prisimink tai
ir
Ar ne tas pats. Pavyzdžiui, jei - tada išsigimęs
, a
(paprastai tariant).

Kur: *;

* ;*
.

Def . Visuma
tarpinis atstumas vadinamas intervalo padalijimu , jei: *;

*
; *
; *
; *
.

Kiekis
vadinamas skaidinio parametru P(kur
).

Def . Skaldymas vadinamas skaidinio patikslinimu jei visi skaidinio elementai gautas padalijus suskaidytus elementus .

Nurodoma:
... Skaityti: mažesnis arba didesnis .

Kalbant apie didesnius ir mažesnius santykius, tai tiesa:

*. tranzityvumas -; *.
;

*.

; *.

|
.

§. Kelių integralų apibrėžimas

Leisti būti
- mediena (tarpas) ,
- plyšio padalijimas Aš... Kiekvienu skaidinio intervalu pažymėkite tašką
.

Mes gauname
padalintas pažymėtais taškais
.

Kiekis
funkcijai vadinama integralia Riemann suma f (x) intervalu Aš padalijant pažymėtais taškais
.

Def :
=
=
.

Žymėjimas - funkcijų rinkinys, integruotas juostoje Aš mes užsirašome:

Def : ε > 0 δ>0<.

Jei dėl funkcijos f(x) įjungta Aš ir skaldymas
- žymėti
- didžiausia ir mažiausia funkcijos vertė f(x) įjungta Aš k tada kiekiai
=
ir
=
vadinamos apatine ir viršutine Darboux sumomis.

§. Daugialypio integralo egzistavimo Darboux kriterijus.

T 0 . Kad veiktų
buvo integruotas bare (tie.
) to reikia ir pakanka

. Δ▲.

Nustatyta funkcijos integracija per juostą Euklido erdvėje. Kaip integruoti funkciją per savavališką ribotą rinkinį iš Euklido erdvės?

Apibrėžkime funkcijos integralą f pagal rinkinį
.

Def : Leisti būti
ir
- ribotas, t.y.
... Funkcija
vadinama charakterine aibės funkcija M.

Tada:
≡
.

Aibės integralo apibrėžimas nepriklauso nuo to, kurioje juostoje yra M pasirinktas, t.y.

.

Tai reiškia, kad integralo apibrėžimas aibėje yra teisingas.

Būtina integravimo sąlyga. Kad veiktų f(x) įjungta M būti integruotam, tai būtina f(x) apsiribojo M. Δ▲.

§. Kelių integralų savybės.

1  . Tiesiškumas: daug R M funkcijos, integruotos į rinkinį M - linijinis

erdvė, ir
- linijinis funkcinis.

2  . Normalizavimo sąlyga:
... Kita žymėjimo forma
iš tikrųjų nustato savavališkos aibės iš Euklido erdvės matą.

3  . Jei integralas virš Lebesgue mato rinkinio nulio egzistuoja, tada jis

yra nulis.

Pastaba: Daug M vadinama Lebesgue mato aibės aibė,

jei

toks kad
ir
.

4  . a.;b.;

v. jei
ir - nuo nulio atskirtas M, tada

5  .
ir f=g p.c. (beveik visur) M, tada
.

6  . Pridėtumas: jei
ir
tada

Apskritai:
.

Δ. Iš lygybės seka: ▲

7  . Monotoniškas:
ir
tada
.

8  . Nelygybių integracija: jei
ito

9  . Leisti būti

... Į
, būtina ir pakanka, kad būtų rinkinio vidinis taškas M, kur f (x)> 0 ir yra ištisinis.

10  . Integruotos funkcijos modulio integruotumas:
.

11  . Vidutinė teorema:
,
ant M išsaugo ženklą ir
, tada

Jei rinkinys M- prijungtas ir f(x) Veikia nuolat
tada
toks kad
.

12  . Kad neneigiamos funkcijos integralas būtų lygus 0

reikalingas ir pakankamas f(x) = 0 beveik visur M.

13  . Fubini teorema. Dvigubam integralui:

Tegul regionas
- stačiakampis :. Tada, esant vidiniams pavieniams integralams, norint rasti dvigubą integralą, galima pereiti prie pakartotinės integracijos (žr. A pav.):

, arba

Jei integracijos sritis nėra stačiakampis, Fubini teorema vis dar galioja ir turi tokią formą (žr. B pav.):

. (*)

Pastaba: Išorinės integracijos ribos turėtų būti pastovios, vidinės integracijos ribos gali priklausyti nuo kintamojo, per kurį integracija dar turi būti atlikta.

Formulę (*) galima gauti naudojant aibei būdingą funkciją D.

Kelių integralams:

Leiskite kai kuriuos Euklido erdvių pogrupius ir ... Mes apibrėžiame šių rinkinių Dekarto sandaugą, kuri yra Euklido erdvės pogrupis
:.

Tada Fubini teorema
atrodo kaip:
.

Teorema galioja ir juostoms X ir Y ir sudėtingesnėms konfigūracijoms.

Pavyzdžiai:

1 0 . Apskaičiuoti
jei regiono siena
pateiktos lygtimis:

... Rasdami kreivių, apibrėžiančių regiono ribą, susikirtimo taškus, gauname du taškus:

... Tada galimas integracijos ribų išdėstymas, kai pereinama prie integruotų integralų, suteikia:

a).
;

0 . Pakeiskite integravimo tvarką iš naujo:

–

Receptas: Nustatant integracijos dvigubo integralo ribas, rekomenduojama pradėti nuo išorinių integracijos ribų.

0 . Apskaičiuoti:

, jei

Perėjimas prie itegralaus integralo suteikia:
.

Šiuo atveju trigubame integrale ribų išdėstymas turi prasidėti nuo vidinių integracijos ribų. Tada projektuokite teritoriją V lėktuve xOi

ribų nustatymas rajone D- guli lėktuve xOi.

4 0 . Pakeiskite integravimo tvarką iš naujo:
.

Pakalbėkime šiek tiek išsamiau apie Ostrogradskio kūrinius, susijusius su keliais integralais.

Ostrogradskio formulė, skirta trigubam integralui paversti dvigubu integralu, kurią paprastai rašome formoje

kur div A yra vektoriaus A lauko nukrypimas,

An yra vektoriaus A skaliarinis sandauga iš ribinio paviršiaus išorinio normaliojo n vieneto vektoriaus; matematinėje literatūroje jis dažnai anksčiau buvo siejamas su Gauso ir Greeno pavadinimais.

Tiesą sakant, Gausso darbe apie sferoidų trauką galima įžvelgti tik labai ypatingus (1) formulės atvejus, pavyzdžiui, kai P = x, Q = R = 0 ir tt Kalbant apie J. Greeną, jo darbe apie elektros teoriją ir apskritai nėra (1) formulės magnetizmo; jis išvedė kitą ryšį tarp trigubo ir dvigubo integralo, būtent, Greeno formulę Laplaso operatoriui, kurią galima parašyti tokia forma

Žinoma, nustatant formulę (1) galima išvesti iš (2)

ir taip pat galite gauti formulę (2) iš formulės (1), tačiau Greenui net nekilo mintis tai padaryti.

kur integralas per tūrį yra kairėje, o integralas virš ribinio paviršiaus yra dešinėje, ir tai yra išorinio normalumo krypties kosinusai.

Paryžiaus Ostrogradskio rankraščiai visiškai užtikrintai liudija, kad tiek integraliosios teoremos (1) atradimas, tiek pirmasis perdavimas priklauso jam. Ji pirmą kartą buvo išreikšta ir įrodyta, kaip ir dabar, kai tai daroma 1826 m. Vasario 13 d. Paryžiaus mokslų akademijai pateiktame „vientiso skaičiavimo teoremos įrodyme“, po kurio jis vėl buvo suformuluotas toje „Memuaro“ dalyje. apie šilumos sklidimą viduje kietos medžiagos“, Kurį Ostrogradskis pristatė 1827 m. Rugpjūčio 6 d.„ Memuarai “buvo pateikti Furjė ir Poisson peržiūrai, o pastarasis tikrai jį perskaitė, ką liudija įrašas abiejų rankraščio dalių pirmuosiuose puslapiuose. Žinoma, Poissonas net nemanė sau priskirti teoremos, kurią jis sutiko Ostrogradskio darbe prieš dvejus metus iki savo darbo apie elastingumo teoriją pristatymo.

Kalbant apie kūrinių, susijusių su daugybe Ostrogradskii ir Green integralo, ryšį, prisimename, kad „Pastaboje apie šilumos teoriją“ buvo išvesta formulė, apimanti paties Greeno formulę, kaip labai ypatingą atvejį. Dabar neįprasta Cauchy simbolika, kurią Ostrogradskis naudojo „Pastaboje“, dar neseniai slėpė šį svarbų atradimą nuo tyrėjų. Žinoma, Greene'as išlaiko garbę atrasti ir pirmą kartą 1828 m. Paskelbti formulę, skirtą jo vardą turinčiam Laplaso operatoriui.

Trigubo integralo pavertimo dvigubu integralu formulės atradimas padėjo Ostrogradskii išspręsti n-kartų integralo keitimo problemą, būtent, išvesti bendrą skirtumo tipo išraiškos integralo transformacijos formulę per n matmenų sritį ir integralą virš ribojančio super paviršiaus S su lygtimi L (x, y, z, ...) = 0. Jei laikysimės ankstesnio žymėjimo, tada formulė turi formą

Tačiau Ostrogradskis nenaudojo geometrinių vaizdų ir terminų, kuriuos naudojame: daugiamatių erdvių geometrija tuo metu dar neegzistavo.

Memuare apie kelių integralų variacijų skaičiavimą nagrinėjami dar du svarbūs tokių integralų teorijos klausimai. Pirma, Ostrogradskis išvedė kintamųjų keitimo formulę daugialypiame integrale; antra, pirmą kartą jis pateikia išsamų ir tikslų n-kartų integralo skaičiavimo metodo aprašymą, pasitelkdamas n nuoseklių kiekvieno kintamojo integracijų per atitinkamas ribas. Galiausiai, iš šiame memuare esančių formulių nesunku nuspręsti Pagrindinė taisyklė diferenciacija daugiamatio integralo parametro atžvilgiu, kai nuo šio parametro priklauso ne tik integralas, bet ir integracijos srities riba. Ši taisyklė išplaukia iš prisiminimų formulių taip natūraliai, kad vėliau matematikai netgi tapatino ją su viena iš šio prisiminimų formulių.

Ostrogradskis specialų darbą skyrė kintamųjų keitimui keliuose integraluose. Dvigubam integralui atitinkama taisyklė buvo išvesta naudojant formalias Eulerio, trigubo integralo - Lagrange'o transformacijas. Tačiau, nors Lagrange'o rezultatas teisingas, jo samprotavimai nebuvo tikslūs: atrodė, kad jis remiasi tuo, kad tūrio elementai senuose ir naujuose kintamuosiuose - koordinatėse - yra lygūs vienas kitam. Ostrogradskis padarė panašią klaidą ką tik minėtos kintamųjų keitimo taisyklės išvesties pradžioje. Straipsnyje „Dėl kintamųjų transformacijos keliuose integraluose“ Ostrogradskis atskleidė Lagrange'o klaidą, taip pat pirmą kartą pristatė tą aiškų geometrinį kintamųjų transformavimo į dvigubą integralą metodą, kuris taip pat pateikiamas kiek griežtesne forma mūsų vadovuose. Būtent, keičiant integralo kintamuosius formulėmis, integracijos sritis padalijama iš dviejų sistemų u = const, v = const koordinačių linijų į begalybės mažus kreivinius keturkampius. Tada integralas gali būti gautas iš pradžių sudėjus tuos jo elementus, kurie atitinka be galo siaurą kreivinę juostą, ir tada, toliau skaičiuojant elementus pagal juosteles, kol jie visi išeikvojami. Paprastas skaičiavimas suteikia plotą, kuris gali būti laikomas lygiagretainiu iki nedidelės aukštesnės eilės, išraiška, kur, pasirenkama taip, kad plotas būtų teigiamas. Dėl to mes gauname gerai žinomą formulę

Dviejų kintamųjų funkcijai, apibrėžtai kaip z = f(x, y) .

Dvigubas integralas parašytas taip:

Čia D- plokščia figūra, apribota linijomis, kurių išraiškos (lygybės) pateikiamos atliekant dvigubo integralo skaičiavimo užduotį. Kairė ir dešinė - lygybės, kuriose kintamasis kairėje x, o aukščiau ir žemiau - lygybės, kuriose yra kintamasis kairėje y... Ši vieta ir dar daugiau - viena iš svarbiausių norint suprasti dvigubo integralo skaičiavimo techniką.

Apskaičiuokite dvigubą integralą - reiškia rasti skaičių, lygų minėto paveikslo plotui D .

Kol neliesime dvigubo integralo apibrėžimai , bet mes išmoksime jį apskaičiuoti. Lengviau suprasti, kas yra dvigubas integralas, kai išsprendėte keletą uždavinių, kad jį apskaičiuotumėte, todėl šios pamokos pabaigoje rasite dvigubo integralo apibrėžimą. Bėgdami šiek tiek į priekį, galime tik pastebėti, kad dvigubo integralo apibrėžimas taip pat yra susijęs su minėtu skaičiumi D .

Jei figūra D yra stačiakampis, visos jį ribojančios linijos yra tiesios. Jei figūra D- yra kreivinis, tada kairėje ir dešinėje jis ribojamas tiesiomis linijomis, o aukščiau ir žemiau - išlenktomis linijomis, nurodytomis užduotyje nurodytomis lygtimis. Būna atvejų, kai figūra D- trikampis, bet apie tokius atvejus kiek toliau.

Todėl norint apskaičiuoti dvigubą integralą, būtina surūšiuoti linijas, ribojančias figūrą D, kuris turi griežtą pavadinimą - integracijos sritis. Rūšiuoti į kairę ir į dešinę, į viršų ir apačią. To reikės, kai dvigubą integralą sumažinant iki itegralaus integralo - dvigubo integralo apskaičiavimo metodas.

Stačiakampio ploto korpusas:

Išlenktos srities atvejis:

Ir tai jau yra tam tikrų mums pažįstamų integralų sprendimas, kuriame pateikiamos viršutinės ir apatinės integracijos ribos. Išraiškos, apibrėžiančios figūrą ribojančias linijas D, bus integracijos ribos įprastiems apibrėžtiems integralams, prie kurių jau artėjame.

Dvigubo integralo sumažinimas iki kartotinio integralo

Stačiakampio formos dėklas

Tegul tokia funkcija turi dvigubą integralą

Į apskaičiuokite šį dvigubą integralą , būtina jį sumažinti iki pakartotinio integralo, kuris turi formą

Pirmiausia reikia apskaičiuoti vidinį (dešinįjį) apibrėžtąjį integralą, tada - išorinį (kairįjį) apibrėžtąjį integralą.

Galite pakeisti vaidmenis x ir y

1 pavyzdys. Apskaičiuokite dvigubą integralą

Mes apskaičiuojame vidinį (dešinįjį) integralą, darant prielaidą, kad y yra konstanta. Mes gauname.

2 pavyzdys. Apskaičiuokite dvigubą integralą

Sprendimas. Sumažinkite šį dvigubą integralą iki itegralaus integralo

Piešinyje mes kuriame integracijos sritį:

Dabar apskaičiuojame ką tik apskaičiuoto vidinio (dešiniojo) integralo išorinį (kairįjį) integralą:

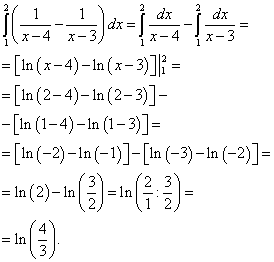
Rezultatas bus šio dvigubo integralo sprendimas.

Dvigubą integralą apskaičiuokite patys ir tada pamatysite sprendimą

Išlenktos arba trikampės srities atvejis

Dar kartą duokime dviejų kintamųjų funkciją f(x, y) , ir apribojimai D: jau šiek tiek kitokio pobūdžio:

Šis įrašas reiškia, kad figūra Dį kairę ir į dešinę, kaip ir tiesios srities atveju - tiesios linijos x = a ir x = b, bet žemiau ir aukščiau yra kreivės, pateiktos lygtimis ir. Kitaip tariant, ir yra funkcijos.

Tegul tokia funkcija taip pat turi dvigubą integralą

Norint apskaičiuoti šį dvigubą integralą, būtina jį sumažinti iki pakartotinio integralo, kuris turi formą

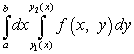Čia yra integracijos ribos a ir b yra skaičiai ir yra funkcijos. Trikampio regiono atveju viena iš funkcijų arba yra tiesios linijos lygtis. Šis atvejis bus analizuojamas 3 pavyzdyje.

Kaip ir tiesiaeigio regiono atveju, pirmiausia turite apskaičiuoti dešinįjį apibrėžtąjį integralą, tada kairįjį apibrėžtąjį integralą.

Taip pat galite keistis vaidmenimis x ir y... Tada kartotinis integralas turės formą

Toks kartotinis integralas turi būti sprendžiamas vienodai: pirma, vidinis (dešinysis) integralas, tada išorinis (kairysis) integralas.

5 pavyzdys. Apskaičiuokite dvigubą integralą

Sprendimas. Sumažinkite šį dvigubą integralą iki itegralaus integralo

Brėžinyje mes kuriame integracijos sritį ir matome, kad ji yra trikampė:

Mes apskaičiuojame vidinį (dešinįjį) integralą, laikydami x konstanta. Mes gauname.

Dabar apskaičiuojame ką tik apskaičiuoto vidinio (dešiniojo) integralo išorinį (kairįjį) integralą. Pirma, šį integralą vaizduojame kaip integralo sumą:

Mes apskaičiuojame pirmąjį terminą:

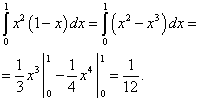
Mes apskaičiuojame antrąjį terminą:

Mes apskaičiuojame trečiąjį terminą:

Mes gauname sumą, kuri bus šio dvigubo integralo sprendimas:

6 pavyzdys. Apskaičiuokite dvigubą integralą

Sprendimas. Sumažinkite šį dvigubą integralą iki itegralaus integralo

Piešinyje mes kuriame integracijos sritį:

Mes apskaičiuojame vidinį (dešinįjį) integralą, laikydami x konstanta. Mes gauname.

Dabar apskaičiuojame ką tik apskaičiuoto vidinio (dešiniojo) integralo išorinį (kairįjį) integralą:

Rezultatas bus šio dvigubo integralo sprendimas.

x- teisinga ir neteisinga, y- teisingos ir neteisingos integracijos sritys

Taip atsitinka, kad dvigubo integralo integracijos sritis yra apribota tokiomis linijomis, kad atsiranda poreikis suskaidyti integracijos sritį į dalis ir kiekvieną atitinkamą integruotą integralą išspręsti atskirai. Tai yra atvejai, kai:

1) integracijos sritis yra figūra, turinti dvi ar daugiau tiesių ar išlenktų linijų apatinės arba viršutinės (kairės arba dešinės) sienos formos;

2) integracijos sritis yra figūra, kurios kraštinės tiesios susikerta daugiau nei dviejuose taškuose.

Jei tai, kas išdėstyta aukščiau, taikoma integracijos regiono kairiajai arba dešinei ribai, tai yra apribojimams, kuriuos nustato linijos, išreikštos x, tada vadinamas integracijos regionas x-negerai. Jei tiesus y = y0 kerta atitinkamą ribą tik viename taške, o jei riba yra tik viena tiesė ar kreivė, tada integracijos sritis vadinama x- teisingai

Panašiai, jei siena apibrėžta linijomis, išreikštomis per y, tiesiai x = x0 susikerta daugiau nei viename taške arba jei daugiau kaip viena tiesė ar kreivė tarnauja kaip riba, integracijos sritis vadinama y-negerai. Parodykite ženklus dabar y-teisinga sritis, matyt, yra gana paprasta.

Iki šiol mes apžvelgėme pavyzdžius su x- neteisinga ir y- teisingos integracijos sritys. Dabar apsvarstykime atvejus, kai pažeidžiama teisingumo sąlyga.

7 pavyzdys. Apskaičiuokite dvigubą integralą, kurio integracijos sritį riboja linijos y = x , xy = 1 , y = 2 .

Sprendimas. Integracijos sritis yra y-negerai, nes jos apatinės ribos negalima nustatyti viena eilute y = y(x) ... Kaip matote aukščiau esančiame paveikslėlyje, apatinę sieną sudaro y = x(tamsiai bordo) ir xy= 1 (žalia). Todėl tiesioginis x= 1 (juoda) integracijos regioną galime padalyti į dvi dalis - ir.

Šis dvigubas integralas apskaičiuojamas taip:

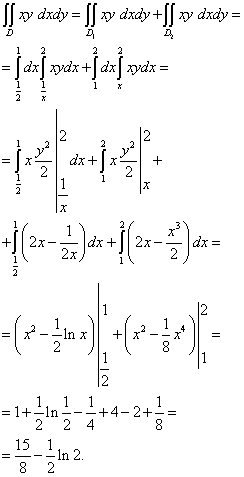
Integracijos tvarkos keitimas

Kaip minėta aukščiau, sumažinus dvigubą integralą į iteratinį integralą, galima pakeisti kintamuosius x ir y vaidmenis arba, kitaip tariant, pakeisti integracijos tvarką.

Integracijos tvarkos pasikeitimą perkeltine prasme galima apibūdinti šiais žodžiais apie „Henrį“: „Taip elgiasi džiunglių gyventojas - žvėris, atsidūręs narve, ir taip elgiasi narvo gyventojas - žmogus, pasiklydęs abejonių džiunglės. "ir tas pats:" Chalmersas suplėšė laišką į tūkstantį mažiausių gabalėlių ir ėmė draskyti savo brangų kilimą, žingsniuodamas pirmyn ir atgal ". ( O.Henry. Scheisrazade Madisono aikštėje.)

Tada, jei kintamojo atžvilgiu turime kairįjį integralą x, o teisingas - iki y, tada pakeitus integracijos tvarką viskas bus atvirkščiai. Tada „naujo“ žaidimo integracijos ribos turėtų būti „pasiskolintos“ iš „senojo“ x, o „naujo“ x integracijos ribos turėtų būti gautos tokia forma atvirkštinė funkcija, išsprendęs x lygtį, kuri nustatė žaidimo ribą.

8 pavyzdys.

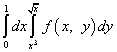Sprendimas. Pakeitus integravimo tvarką, žaidimo integralas tampa kairysis, o integralas virš x - dešinysis. „Naujojo“ žaidimo integracijos ribos bus pasiskolintos iš „senojo“ x, tai yra, apatinė riba lygi nuliui, o viršutinė - vienai. „Seno“ žaidimo integracijos ribos pateikiamos lygtimis ir. Išsprendę šias x lygtis, gauname naujas x integracijos ribas:

(apačioje) ir (viršuje).

Taigi, pakeitus integracijos tvarką, pakartotinis integralas bus parašytas taip:

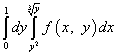Pakeitus dvigubo integralo integracijos tvarką, integracijos regionas dažnai virsta y-negerai arba x- neteisinga (žr. ankstesnę pastraipą). Tada reikia padalinti integracijos sritį į dalis ir kiekvieną atitinkamą itegruojamą integralą išspręsti atskirai.

Kadangi integracijos srities skaidymas į dalis daugeliui studentų kelia tam tikrų sunkumų, neapsiribosime ankstesnėje pastraipoje pateiktu pavyzdžiu, bet apsvarstysime dar porą pavyzdžių.

9 pavyzdys. Pakeiskite pakartotinio integralo integravimo tvarką

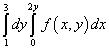Sprendimas. Taigi, šio integruoto integralo integracijos sritį riboja tiesios linijos y = 1 , y = 3 , x = 0 , x = 2y .

Kai integruojama kita tvarka, apatinę regiono ribą sudaro dvi tiesės: AB ir Kr kuriuos pateikia lygtys y= 1 ir y = x/ 2, kurį galima pamatyti žemiau esančiame paveikslėlyje.

Išeitis iš šio netikrumo yra padalinti integracijos regioną į dvi dalis. Integracijos sritis bus padalinta tiesia linija BM... Mes apskaičiuojame naujas integracijos ribas, surasdami atvirkštinę funkciją. Remiantis šiuo sprendimu, pakeistas integracijos eiliškumas bus integruotas į dviejų integralų sumą:

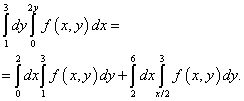
Natūralu, kad tas pats bus dvigubo integralo sprendimas, kuris sumažėja iki itegralaus integralo, pateikto šio pavyzdžio sąlygomis.

10 pavyzdys. Pakeiskite pakartotinio integralo integravimo tvarką

Sprendimas. Taigi, kartotinio integralo integracijos sritis yra ribojama tiesių linijų x = 0 , x= 2 ir kreivės ir.

Kaip matyti paveikslėlyje žemiau, tiesi linija, lygiagreti ašiai 0x, peržengs apatinę integracijos regiono ribą daugiau nei dviejuose taškuose.

Todėl integracijos sritį padalinsime į tris dalis tiesiomis linijomis, kurios paveiksle nubrėžtos juodai. Mes apskaičiuojame naujas integracijos ribas, surasdami atvirkštinę funkciją. Trijų naujų integracijos sričių ribos bus tokios.

Remiantis šiuo sprendimu, pakeistas integracijos eiliškumas bus integruotas į tris integralų sumą:

Ta pati trijų integralų suma bus lygi dvigubam integralui, kuris sumažės iki itegralaus integralo, pateikto šio pavyzdžio sąlygomis.

Ir vis dėlto nenugalimos jėgos aplinkybės dažnai trukdo studentams jau ankstesniame žingsnyje - nustatant integracijos ribas. Nerimas ir sumišimas nėra be jokios priežasties: jei paprastai pakanka pažvelgti į piešinį, kad integracijos regionas būtų padalintas į dalis, ir išspręsti pakartotinį integralą - integralo lentelę, tada norint nustatyti integracijos ribas reikia tam tikros mokymo patirties. . Pažvelkime į pavyzdį, kuriame mes sutelksime dėmesį tik į integracijos ribų išdėstymą ir beveik automatiškai į domeno skaidymą ir praleisime patį sprendimą.

11 pavyzdys. Raskite dvigubo integralo integracijos ribas, jei integracijos regionas D yra nustatytas taip:

y - 2x ≤ 0;
2m - x ≥ 0;
xy ≤ 2.

Sprendimas. Aiškiai (per x ir y„be priemaišų“), integracijos sritį ribojančios linijos nenurodytos. Kadangi x atveju jie dažniausiai pasirodo kaip tiesios linijos, liečiančios žaidimo metu išreikštas viršutines ir apatines ribas, tada eisime būtent šiuo keliu. Be to, keisdami integracijos tvarką, gauname tos pačios srities integracijos regioną. Išspręskime žaidimo nelygybę ir gaukime:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

Mes piešiame gautas linijas brėžinyje. X integracijos ribos iš tikrųjų yra linijos x= 0 ir x= 2. Tačiau integracijos sritis pasirodė esanti y-negerai, nes jos viršutinės ribos negalima nustatyti viena eilute y = y(x) .

Atsisiųskite iš „Depositfiles“

Paskaitos 5-6

2 tema. Keli integralai.

Dvigubas integralas.

Kontroliniai klausimai.

1. Dvigubas integralas, jo geometrinė ir fizinė reikšmė

2. Dvigubo integralo savybės.

3. Dvigubo integralo skaičiavimas stačiakampėmis koordinatėmis.

4. Kintamųjų keitimas dvigubame integrale. Dvigubo integralo apskaičiavimas polinėse koordinatėse.

Leiskite funkcijai z = f (x , y) yra apibrėžtas uždaroje uždaroje srityje D lėktuvas. Išardykime teritoriją D savavališkai n elementarūs uždari regionai  1 , … , n su sritimis   1 , …,   n ir skersmenys d 1 , …, d n atitinkamai. Mes žymime d didžiausias iš regionų skersmens  1 , … ,  n... Kiekvienoje srityje  k pasirinkti savavališką tašką P k (x k , y k) ir komponuoti vientisą sumą funkcija f(x, y)

S =
(1)

Apibrėžimas. Dvigubas integralas funkcija f(x, y) pagal sritį D vadinama integralios sumos riba

, (2)

jei jis egzistuoja.

Komentuoti. Integrali suma S priklauso nuo to, kaip regionas yra padalintas D ir taškų pasirinkimas P k (k=1, …, n). Tačiau riba
, jei jis egzistuoja, nepriklauso nuo regiono skaidymo metodo D ir taškų pasirinkimas P k .

Pakankama sąlyga dvigubo integralo egzistavimui. Dvigubas integralas (1) egzistuoja, jei funkcija f(x, y) tęstinis D išskyrus ribotą skaičių vienetų lygių kreivių ir yra apribotas D... Toliau darysime prielaidą, kad visi svarstomi dvigubi integralai egzistuoja.

Dvigubo integralo geometrinė reikšmė.

Jei f(x, y) ≥0 rajone D, tada dvigubas integralas (1) yra lygus paveiksle pavaizduoto „cilindrinio“ korpuso tūriui:

V =
(3)

Cilindrinis kūnas iš apačios yra ribojamas srities D, iš viršaus  paviršiaus dalis z = f (x , y), šonuose  vertikaliais linijų segmentais, jungiančiais šio paviršiaus ir regiono ribas D.

Dvigubo integralo fizinė reikšmė. Plokščių plokščių masė.

Leiskite duoti plokščią plokštelę D su žinoma tankio funkcija γ ( NS,adresu), tada padalinkite plokštę D į dalis D i ir pasirenkant savavališkus taškus
, gauname plokštelės masę
arba, lyginant su (2) formule:

(4)

4. Kai kurios dvigubo integralo savybės.

Tiesiškumas. Jei SU Tada yra skaitinė konstanta

Pridėtumas. Jei sritis D „Padalinti“ į sritis D 1 ir D 2, tada

3) Riboto ploto plotas D yra lygus

(5)

Dvigubo integralo skaičiavimas stačiakampėmis koordinatėmis.

Tegul regionas yra duotas

1 paveikslas

D = { (x , y ): a ≤ x ≤ b , φ 1 (x ) ≤ y≤ φ 2 (x ) } (6)

Regionas D uždengta juostele tarp tiesių linijų x = a , y = b, iš apačios ir iš viršaus riboja atitinkamai kreivės y = φ 1 (x ) ir y = φ 2 (x ) .

Dvigubas integralas (1) virš ploto D(4) yra apskaičiuojamas pereinant prie iteralaus integralo:

(7)

Šis kartotinis integralas apskaičiuojamas taip. Pirmiausia apskaičiuojamas vidinis integralas

pagal kintamąjį y, kur x laikomas pastoviu. Rezultatas yra kintamojo funkcija x, tada apskaičiuojamas šios funkcijos „išorinis“ integralas kintamojo atžvilgiu x .

Komentuoti. Perėjimo prie iteralaus integralo procesas pagal formulę (7) dažnai vadinamas integracijos ribų išdėstymu dvigubame integrale. Nustatant integracijos ribas, reikia turėti omenyje du dalykus. Pirma, apatinė integracijos riba neturėtų viršyti viršutinės, antra, išorinio integralo ribos turėtų būti pastovios, o vidinis integralas paprastai turėtų priklausyti nuo išorinio integralo integravimo kintamojo.

Dabar leiskite regionui D turi formą

D = { (x , y ) : c ≤ y ≤ d , ψ 1 (y ) ≤ x ≤ ψ 2 (y ) } . (8)

Tada

. (9)

Tarkime, kad sritis D gali būti pavaizduotas (6) ir (8) pavidalu vienu metu. Tada lygybė

(10)

Perėjimas iš vieno iteralaus integralo į kitą lygybėje (10) vadinamas keičiant integracijos tvarką dvigubame integrale.

Pavyzdžiai.

1) Pakeiskite integralo integravimo tvarką

Sprendimas. Iš pasikartojančio integralo formos randame regioną

D = { (x , y ): 0 ≤ x ≤ 1, 2 x ≤ y≤ 2 } .

Nubrėžkime plotą D... Iš paveikslo matome, kad ši sritis yra horizontalioje juostoje tarp tiesių linijų y =0, y= 2 ir tarp eilučių x =0 ir x= D

Kartais kintamieji keičiami siekiant supaprastinti skaičiavimus:

,
(11)

Jei funkcijos (11) yra nuolat diferencijuojamos, o determinantas (Jokūbo) nagrinėjamoje srityje yra nulis:

(12)

Rusijos Federacijos švietimo ir mokslo ministerija

Kursinis darbas

Disciplina: aukštoji matematika

(Pagrindinis linijinis programavimas)

Tema: KELIŲ INTEGRALŲ

Baigta: ______________

Mokytojas: ___________

Data ___________________

Įvertinimas _________________

Parašas ________________

VORONEŽAS 2008 m

1 Keli integralai

1.1 Dvigubas integralas

1.2 trigubas integralas

1.3 Keli integralai kreivinėmis koordinatėmis

1.4 Kelių integralų geometrinės ir fizinės programos

2 Kreiviniai ir paviršiaus integralai

2.1 Kreiviniai integralai

2.2 Paviršiaus integralai

2.3 Geometrinės ir fizinės programos

Bibliografija

1 Keli integralai

1.1 Dvigubas integralas

Oxy plokštumoje apsvarstykite uždarą sritį D, apribotą linija L. Šią sritį dalijame keliomis linijomis į n dalis

, o atitinkami didžiausi atstumai tarp taškų kiekvienoje iš šių dalių bus žymimi d 1, d 2, ..., d n. Kiekvienoje dalyje pasirinkite tašką Р i.

Funkcija z = f (x, y) bus pateikta D srityje. Pažymėkime f (P 1), f (P 2),…, f (P n) šios funkcijos reikšmes pasirinktuose taškuose ir sudarykime f (P i) formos produktų sumą ΔS i :

, (1)

vadinama integruota funkcijos f (x, y) suma D srityje.

Jei yra ta pati vientisų sumų riba (1)

ir kuris nepriklauso nei nuo domeno D padalijimo į dalis metodo, nei nuo taškų P i pasirinkimo juose, tada jis vadinamas dvigubu funkcijos f (x, y) integralu per domeną D ir yra žymimas

. (2)

Dvigubo integralo skaičiavimas ties D riba, apribota linijomis

x = a, x = b (a< b), где φ 1 (х) и φ 2 (х) непрерывны на (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:

(3)

1.2 Trigubas integralas

Trigubo integralo sąvoka įvedama pagal analogiją su dvigubu integralu.

Tegul tam tikras domenas V pateikiamas erdvėje, kurią riboja uždaras paviršius S. Apibrėžkime tęstinę funkciją f (x, y, z) šioje uždaroje srityje. Tada mes padalijame regioną V į savavališkas dalis Δv i, darant prielaidą, kad kiekvienos dalies tūris yra lygus Δv i, ir sudarome vientisą formos sumą

, (4)

Riboti

vientisos sumos (11), kurios nepriklauso nuo domeno V padalijimo būdo ir taškų P i pasirinkimo kiekviename šio domeno padomenyje, vadinamas trigubu funkcijos f (x, y, z) integralu per V domenas:

. (5)

Funkcijos f (x, y, z) trigubas integralas virš srities V yra lygus trigubam integralui toje pačioje srityje:

. (6)

1.3 Keli integralai kreivinėmis koordinatėmis

Įveskime plokštumoje kreivines koordinates, vadinamas polinėmis koordinatėmis. Pasirinkite tašką O (polius) ir iš jo kylantį spindulį (polinė ašis).

Ryžiai. 2 pav 3

Taško M koordinatės (2 pav.) Bus MO segmento ilgis - polinis spindulys ρ ir kampas φ tarp MO ir polinės ašies: M (ρ, φ). Atkreipkite dėmesį, kad visuose plokštumos taškuose, išskyrus polių, ρ> 0 ir polinis kampas φ bus laikomi teigiamais, kai matuojama prieš laikrodžio rodyklę, ir neigiama, kai matuojama priešinga kryptimi.

Taško M poliarinės ir stačiakampės koordinačių santykį galima nustatyti suderinus Dekarto koordinačių sistemos kilmę su poliu, o teigiamą pusiaksį Ox - su poline ašimi (3 pav.). Tada x = ρcosφ, у = ρsinφ. Iš čia

, tg.

Domene, apribotame kreivėmis ρ = Φ 1 (φ) ir ρ = Φ 2 (φ), kur φ 1< φ < φ 2 , непрерывную функцию z = f(φ, ρ) (рис. 4).

(7)

Trimatėje erdvėje įvedamos cilindrinės ir sferinės koordinatės.

Taško P (ρ, φ, z) cilindrinės koordinatės yra šio taško projekcijos Oxy plokštumoje ir šio taško z taikinio polinės koordinatės ρ, φ (5 pav.).

5 pav. 6 pav

Perėjimo nuo cilindrinių koordinačių prie stačiakampių koordinačių formulės gali būti nurodytos taip:

x = ρcosφ, y = ρsinφ, z = z. (aštuoni)

Sferinėse koordinatėse taško padėtį erdvėje lemia linijinė koordinatė r - atstumas nuo taško iki Dekarto koordinačių sistemos (arba sferinės sistemos poliaus) kilmės, φ - polinis kampas tarp teigiamo pusašis Ox ir taško projekcija į plokštumą Oxy, o θ - kampas tarp teigiamos ašies Оz pusašio ir atkarpos OP (6 pav.). Kurioje

Nustatykime perėjimo iš sferinių koordinačių į Dekarto koordinates formules:

x = rsinθcosφ, y = rsinθsinφ, z = rcosθ. (devyni)

Tada trigubo integralo perėjimo prie cilindrinių ar sferinių koordinačių formulės atrodys taip: