Predaje više integrala, dvostruki integral. Izračunavanje dvostrukih integrala: teorija i primjeri Rješavanje više integrala

Def . Neka bude,
,

.

Skup se naziva zatvoreni razmak ili zatvorena šipka .

Skup se naziva otvoreni jaz

ili otvoreni bar u .

Def . Mjerenje intervala i količina se naziva:

(Preciznije
).

Def . Ako
takav da
zatim interval naziva se degenerirano i
.

Svojstva mjere razmaka:

a). Pozitivnost:
, i
ako i samo ako - je degeneriran.

b). Pozitivna ujednačenost :.

v). Aditivnost:

* for
takav da
;

* for
i

.

G). Monotonost mjere :.

Def . Promjer šipke (razmak) je vrijednost:

Zapiši to
i
Nisu ista stvar. Na primjer, ako - degeneriran, dakle
, a
(općenito govoreći).

Pri čemu: *;

* ;*
.

Def . Agregat
pod-razmak naziva se cijepanje intervala , ako: *;

*
; *
; *
; *
.

Količina
naziva se parametar particije P(pri čemu
).

Def . Cijepanje naziva se poboljšanje particije ako svi elementi particije dobiveno cijepanjem podijeljenih elemenata .

Označeno je:
... Pročitajte: manji ili veće .

Za odnos veći-manji, istina je:

*. tranzitivnost -; *.
;

*.

; *.

|
.

§. Definicija višestrukog integrala

Neka bude
- drvo (otvor) u ,
- cijepanje jaza I... U svakom od intervala particije označite tačku
.

Dobijamo
podeljeno sa označenim tačkama za
.

Količina
naziva se integralni Riemannov zbroj za funkciju f (x) na intervalu I podjelom sa označenim tačkama
.

Def :
=
=
.

Označavanje - skup funkcija integriranih na traci I zapisujemo:

Def : ε > 0 δ>0<.

Ako je za funkciju f(x) uključeno I i cijepanje
- označiti sa
- najveća i najmanja vrijednost funkcije f(x) uključeno I k zatim količine
=
i
=
nazivaju se donja i gornja Darbouxova suma.

§. Darbouxov kriterij postojanja višestrukog integrala.

T 0 . Za funkcioniranje
je bio integriran na šipku (oni.
) je potrebno i dovoljno da

. Δ▲.

Određena je integracija funkcije preko šipke u euklidskom prostoru. Kako integrirati funkciju preko proizvoljnog ograničenog skupa iz euklidskog prostora?

Definirajmo integral funkcije f po setu
.

Def : Neka bude
i
- ograničeno, tj.
... Funkcija
naziva se karakteristična funkcija skupa M.

Zatim:
≡
.

Definicija integrala nad skupom ne zavisi od toga koja traka sadrži M odabrana, tj.

.

To znači da je definicija integrala nad skupom tačna.

Neophodan uslov za integrabilnost. Za funkcioniranje f(x) uključeno M da budu integrirane, potrebno je da f(x) bio je ograničen na M. Δ▲.

§. Svojstva više integrala.

1  . Linearnost: Mnogi R M funkcije integrirane na skupu M - linearno

prostor, i
- linearno funkcionalan.

2  . Uslovi normalizacije:
... Drugi oblik notacije
zapravo određuje mjeru proizvoljnog skupa iz euklidskog prostora.

3  . Ako postoji integral nad nizom Lebesgueove mjere nula, onda on postoji

je nula.

Bilješka: Mnogo M naziva se skup Lebesgueove mjere nula,

ako

takav da
i
.

4  . a.;b.;

v. ako
i - odvojeno od nule sa M, onda

5  .
i f=g p.c. (skoro svuda) na M, onda
.

6  . Aditivnost: Ako
i
zatim

Uglavnom:
.

Δ. Iz jednakosti slijedi: ▲

7  . Monotonski:
i
zatim
.

8  . Integracija nejednakosti: ako
ito

9  . Neka bude

... To
, potrebno je i dovoljno da postoji unutarnja točka skupa M, pri čemu f (x)> 0 i kontinuirano je.

10  . Integriranost modula integrirane funkcije:
.

11  . Prosječna teorema:
,
uključeno Mčuva znak i
, onda

Ako je skup M- povezani i f(x) Neprekidno je uključeno
zatim
takav da
.

12  . Da bi integral nenegativne funkcije bio jednak 0

potrebno i dovoljno da f(x) = 0 skoro svuda M.

13  . Fubinijeva teorema. Za dvostruki integral:

Neka regija
- pravougaonik:. Zatim se, pod uvjetom postojanja internih pojedinačnih integrala, može pronaći dvostruki integral (vidi sliku A):

, ili

Ako domena integracije nije pravokutnik, Fubinijeva teorema i dalje vrijedi i ima oblik (vidi sliku b):

. (*)

Bilješka: Vanjske granice integracije trebaju biti konstante, unutrašnje granice integracije mogu ovisiti o varijabli preko koje se integracija tek treba obaviti.

Formula (*) se može dobiti pomoću karakteristične funkcije skupa D.

Za višestruki integral:

Neka su neki podskupovi euklidskih prostora i ... Definiramo kartezijanski proizvod ovih skupova, koji je podskup euklidskog prostora
:.

Zatim Fubinijeva teorema za
izgleda kao:
.

Teorema vrijedi i za šipke X i Y, i za složenije konfiguracije.

Primjeri:

1 0 . Izračunati
ako je granica regije
date jednačinama:

... Pronalaženjem točaka sjecišta krivulja koje definiraju granicu regije, dobivamo dvije točke:

... Tada mogući raspored granica integracije pri prelasku na ponovljene integrale daje:

a).
;

0 . Promijenite redoslijed integracije u reintegralu:

–

Recept: Prilikom postavljanja granica integracije u dvostruki integral, preporučuje se početi s vanjskim granicama integracije.

0 . Izračunati:

, ako

Prelazak na ponovljene integrale daje:
.

U ovom slučaju, u trostrukom integralu, raspored granica mora započeti unutrašnjim granicama integracije. Zatim projektujte područje V u avionu xOy

postavljanje granica u tom području D- leži u avionu xOy.

4 0 . Promijenite redoslijed integracije u reintegralu:
.

Zadržimo se nešto detaljnije na djelima Ostrogradskog o višestrukim integralima.

Formula Ostrogradskog za pretvaranje trostrukog integrala u dvostruki integral, koju obično zapisujemo u obliku

gdje je div A divergencija polja vektora A,

An je skalarni proizvod vektora A jediničnim vektorom vanjske normale n granične površine; u matematičkoj literaturi često se ranije povezivao s imenima Gauss i Green.

Zapravo, u Gaussovom radu o privlačenju sferoida mogu se vidjeti samo vrlo posebni slučajevi formule (1), na primjer, za P = x, Q = R = 0 itd. Što se tiče J. Greena, u svom radu o teoriji elektriciteta i uopće ne postoji magnetizam formule (1); izveo je još jednu vezu između trojnih i dvostrukih integrala, naime, Grinovu formulu za Laplaceov operator, koja se može zapisati u obliku

Naravno, moguće je izvesti formulu (1) iz (2) postavljanjem

i na isti način možete dobiti formulu (2) iz formule (1), ali Green nije ni pomislio da to učini.

gdje je integral nad volumenom s lijeve strane, a integral s granične površine s desne strane, a to su kosinusi smjera vanjske normale.

Pariški rukopisi Ostrogradskog svjedoče sa potpunom sigurnošću da su i otkriće i prva komunikacija integralne teoreme (1) pripadali njemu. Prvo je izraženo i dokazano, baš kao što je to sada učinjeno u "Dokazu teoreme integralnog računa", predstavljenom Pariškoj akademiji nauka 13. februara 1826. godine, nakon čega je ponovo formulirano u tom dijelu "Memoara" o širenju topline iznutra čvrste materije”, Koji je Ostrogradsky predstavio 6. avgusta 1827.„ Memoar ”je dat na pregled Fourier -u i Poissonu, koji su ga svakako pročitali, o čemu svjedoči unos na prve stranice oba dijela rukopisa. Naravno, Poisson nije ni pomislio da sebi pripiše teoremu koju je upoznao u djelu Ostrogradskog dvije godine prije predstavljanja svog rada o teoriji elastičnosti.

Što se tiče odnosa između radova o višestrukim integralima Ostrogradskog i Greena, podsjećamo da je u "Bilješci o teoriji topline" izvedena formula koja obuhvata Grinovu vlastitu formulu, kao vrlo poseban slučaj. Sada neobična simbolika Cauchyja, koju je Ostrogradsky koristio u "Bilješci", donedavno je skrivala ovo važno otkriće od istraživača. Naravno, Greene zadržava čast otkrića i prve objave 1828. formule za Laplaceove operatore koji nose njegovo ime.

Otkriće formule za pretvaranje trostrukog integrala u dvostruki integral pomoglo je Ostrogradskomu riješiti problem mijenjanja n-složnog integrala, naime, izvesti opću formulu za transformaciju integrala izraza tipa divergencije nad n-dimenzionalnom domenom i integralom preko granične super-površine S s jednadžbom L (x, y, z, ...) = 0. Ako se pridržavamo prethodnog zapisa, tada formula ima oblik

Međutim, Ostrogradsky nije koristio geometrijske slike i pojmove koje mi koristimo: geometrija višedimenzionalnih prostora tada još nije postojala.

U Memoaru o kalkulaciji varijacija više integrala razmatraju se još dva važna pitanja teorije takvih integrala. Prvo, Ostrogradskii izvodi formulu za promjenu varijabli u višedimenzionalnom integralu; drugo, po prvi put daje potpun i tačan opis metode za izračunavanje n-složnog integrala koristeći n uzastopnih integracija po svakoj od varijabli u odgovarajućim granicama. Konačno, iz formula sadržanih u ovim memoarima lako je zaključiti opšte pravilo diferencijacija u odnosu na parametar višedimenzionalnog integrala, kada ne samo integrant već i granica područja integracije ovisi o ovom parametru. Ovo pravilo slijedi iz formula prisutnih u memoarima na tako prirodan način da su ga kasniji matematičari čak poistovjetili s jednom od formula ovih memoara.

Ostrogradskii je posvetio poseban rad promjeni varijabli u više integrala. Za dvostruki integral, odgovarajuće pravilo izvedeno je koristeći formalne transformacije Eulera, za trostruki integral, Lagrangea. Međutim, iako je Lagrangeov rezultat točan, njegovo zaključivanje nije bilo točno: činilo se da je pošao od činjenice da su elementi volumena u staroj i novoj varijabli - koordinate - jednaki jedan drugome. Ostrogradskii je napravio sličnu grešku u upravo spomenutom izvođenju pravila za promjenu varijabli. U članku „O transformaciji varijabli u više integrala“, Ostrogradskiy je otkrio Lagrangeovu grešku i po prvi put predstavio tu jasnu geometrijsku metodu za pretvaranje varijabli u dvostruki integral, koja je, u nešto rigoroznijem obliku, također predstavljena u naše priručnike. Naime, pri promjeni varijabli u integralu po formulama, područje integracije se dijeli koordinatnim linijama dvaju sistema u = const, v = const u beskonačno male krivolinijske četverougle. Tada se integral može dobiti tako da se prvo zbroje oni njegovi elementi koji odgovaraju beskonačno uskoj krivolinijskoj traci, a zatim se nastavlja zbrajanje elemenata po trakama dok se svi ne iscrpe. Jednostavan izračun daje za područje koje se može smatrati paralelogramom do malog višeg reda, izraz gdje je izabran tako da je područje pozitivno. Kao rezultat toga, dobivamo dobro poznatu formulu

Za funkciju dvije varijable definirane kao z = f(x, y) .

Dvostruki integral zapisan je ovako:

Evo D- ravna figura omeđena linijama čiji su izrazi (jednakosti) dati u zadatku izračunavanja dvostrukog integrala. Lijevo i desno - jednakosti u kojima je varijabla s lijeve strane x, a iznad i ispod - jednakosti u kojima se nalazi varijabla s lijeve strane y... Ovo mjesto i dalje - jedno od najvažnijih za razumijevanje tehnike izračunavanja dvostrukog integrala.

Izračunajte dvostruki integral - znači pronaći broj jednak površini navedene figure D .

Dok ne dodirnemo definicije dvostrukog integrala , ali naučit ćemo to izračunati. Lakše je razumjeti šta je dvostruki integral ako ste riješili nekoliko problema za njegov izračun, pa ćete na kraju ove lekcije pronaći definiciju dvostrukog integrala. Trčeći malo unaprijed, možemo samo primijetiti da je definicija dvostrukog integrala također povezana sa gore navedenom figurom D .

Ako je brojka D je pravokutnik, sve linije koje ga omeđuju su ravne linije. Ako je brojka D- je krivolinijski, zatim s lijeve i desne strane omeđen je ravnim linijama, a iznad i ispod - zakrivljenim linijama datim jednakostima danim u zadatku. Postoje trenuci kada se figura D- trokut, ali o takvim slučajevima malo dalje.

Za izračun dvostrukog integrala potrebno je stoga sortirati linije koje ograničavaju sliku D, koji ima strogi naziv - područje integracije. Sortirajte na lijevo i desno i gore i dolje. To će biti potrebno kada reducirajući dvostruki integral na ponovljeni integral - metoda za izračunavanje dvostrukog integrala.

Kućište pravokutnog područja:

Kućište zakrivljene regije:

A ovo je već rješenje nekih nama poznatih integrala u kojima su date gornje i donje granice integracije. Izrazi koji definiraju linije koje vežu oblik D, bit će granice integracije za obične određene integrale, kojima se već približavamo.

Redukcija dvostrukog integrala na ponovljeni integral

Pravougaono kućište

Neka takva funkcija ima dvostruki integral

To izračunaj ovaj dvostruki integral , potrebno ga je svesti na ponovljeni integral, koji ima oblik

Prvo morate izračunati unutrašnji (desni) određeni integral, a zatim - vanjski (lijevi) određeni integral.

Možete promijeniti uloge x i y

Primjer 1. Izračunajte dvostruki integral

Izračunavamo unutrašnji (desni) integral, pretpostavljajući da je y konstanta. Mi primamo.

Primjer 2. Izračunajte dvostruki integral

Rešenje. Svedite ovaj dvostruki integral na ponovljeni integral

Na crtežu gradimo područje integracije:

Sada izračunavamo vanjski (lijevi) integral upravo izračunatog unutrašnjeg (desnog) integrala:

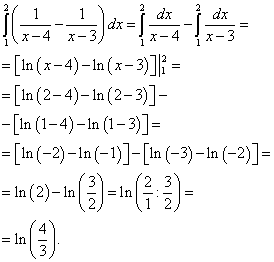
Rezultat će biti rješenje ovog dvostrukog integrala.

Sami izračunajte dvostruki integral, pa pogledajte rješenje

Slučaj zakrivljenog ili trokutastog područja

Neka se opet da funkcija dvije varijable f(x, y) , i ograničenja za D: već malo drugačije vrste:

Ovaj unos znači da je brojka D lijevo i desno vezano, kao u slučaju pravocrtnog područja - ravne linije x = a i x = b, ali ispod i iznad su krivulje koje su date jednadžbama i. Drugim riječima, i jesu funkcije.

Neka takva funkcija ima i dvostruki integral

Za izračun ovog dvostrukog integrala potrebno ga je svesti na ponovljeni integral koji ima oblik

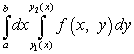Ovdje su granice integracije a i b su brojevi, i i funkcije. U slučaju trokutastog područja jedna od funkcija ili je jednadžba ravne linije. Ovaj slučaj će se analizirati u primjeru 3.

Kao i u slučaju pravocrtnog područja, prvo morate izračunati desni definitivni integral, a zatim lijevi definitivni integral.

Isto tako, možete zamijeniti uloge x i y... Tada će ponovljeni integral imati oblik

Takav ponovljeni integral mora se riješiti na isti način: prvo unutrašnji (desni) integral, zatim vanjski (lijevi) integral.

Primjer 5. Izračunajte dvostruki integral

Rešenje. Svedite ovaj dvostruki integral na ponovljeni integral

Na crtežu gradimo područje integracije i vidimo da je trokutasto:

Izračunavamo unutrašnji (desni) integral, uzimajući u obzir x konstantu. Mi primamo.

Sada izračunavamo vanjski (lijevi) integral upravo izračunatog unutrašnjeg (desnog) integrala. Prvo, ovaj integral predstavljamo kao zbir integrala:

Izračunavamo prvi pojam:

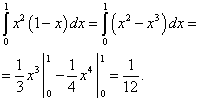
Izračunavamo drugi pojam:

Izračunavamo treći pojam:

Dobivamo zbir koji će biti rješenje ovog dvostrukog integrala:

Primjer 6. Izračunajte dvostruki integral

Rešenje. Svedite ovaj dvostruki integral na ponovljeni integral

Na crtežu gradimo područje integracije:

Izračunavamo unutrašnji (desni) integral, uzimajući u obzir x konstantu. Mi primamo.

Sada izračunavamo vanjski (lijevi) integral upravo izračunatog unutrašnjeg (desnog) integrala:

Rezultat će biti rješenje ovog dvostrukog integrala.

x- tačno i netačno, y- ispravne i netačne domene integracije

Događa se da je područje integracije dvostrukog integrala ograničeno takvim linijama da postaje potrebno podijeliti područje integracije na dijelove i svaki odgovarajući iterovani integral rješavati zasebno. To su slučajevi kada:

1) područje integracije je figura koja ima dvije ili više ravnih ili zakrivljenih linija u obliku donje ili gornje (lijeve ili desne) ivice;

2) regija integracije je figura čija se granica ravnih križa siječe u više od dvije točke.

Ako se gore navedeno odnosi na lijevu ili desnu granicu područja integracije, odnosno ograničenja postavljena linijama izraženim u smislu x, tada se naziva regija integracije x-pogrešno. Ako je ravno y = y0 presijeca odgovarajuću granicu samo u jednoj točki, a ako samo jedna ravna linija ili krivulja služi kao granica, tada se regija integracije naziva x- tačno

Slično, ako je granica definirana linijama izraženima kroz y, ravno x = x0 siječe u više od jedne točke, ili ako više od jedne ravne linije ili krivulje služi kao granica, tada se regija integracije naziva y-pogrešno. Odmah pokažite znakove y-Pravilno područje je, vjerovatno, prilično jednostavno.

Do sada smo razmatrali primjere sa x- netačno i y-pravilna područja integracije. Razmotrimo sada slučajeve kada je povrijeđen uvjet ispravnosti.

Primjer 7. Izračunajte dvostruki integral, čije je područje integracije omeđeno linijama y = x , xy = 1 , y = 2 .

Rešenje. Područje integracije je y-pogrešno, jer se njena donja granica ne može postaviti jednom linijom y = y(x) ... Kao što možete vidjeti na gornjoj slici, donja ivica se sastoji od y = x(tamno bordo) i xy= 1 (zeleno). Zato direktno x= 1 (crno) možemo podijeliti područje integracije na dva dijela - i.

Ovaj dvostruki integral izračunava se na sljedeći način:

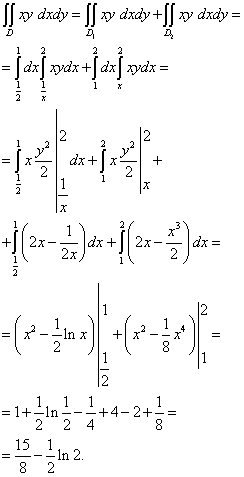
Promjena redoslijeda integracije

Kao što je gore napomenuto, nakon smanjenja dvostrukog integrala na ponovljeni integral, mogu se promijeniti varijable x i y uloge ili, drugim riječima, promijeniti redoslijed integracije.

Promjenu redoslijeda integracije možemo slikovito opisati sljedećim riječima o "Henryju": Ovako se ponaša stanovnik džungle - zvijer, jednom u kavezu, a ovako se ponaša stanovnik kaveza - čovjek, izgubljen u džungli sumnji. "i isto:" Chalmers je rastrgao pismo na hiljadu najmanjih komada i počeo kidati svoj skupi tepih, koračajući napred -nazad po njemu. " ( O.Henry. Šeherezada na Madison Squareu.)

Zatim, ako imamo lijevi integral u odnosu na varijablu x, a desni - mimo y, onda će nakon promjene redoslijeda integracije sve biti obrnuto. Tada granice integracije za "novu" igru treba "posuditi" iz "starog" x, a granice integracije za "novu" x treba dobiti u obliku inverzna funkcija, riješivši jednadžbu za x, koja je postavila granicu za igru.

Primjer 8.

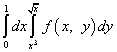Rešenje. Nakon promjene redoslijeda integracije, integral nad igrom postaje lijevo, a integral nad x postaje desno. Granice integracije za "novu" igru posudit će se iz "stare" x, odnosno donja granica jednaka je nuli, a gornja jednaka. Granice integracije za "staru" igru date su jednadžbama i. Nakon što smo riješili ove jednadžbe za x, dobivamo nove granice integracije za x:

(dole) i (gore).

Tako će, nakon promjene redoslijeda integracije, ponovljeni integral biti napisan na sljedeći način:

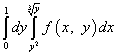Nakon promjene redoslijeda integracije u dvostrukom integralu, integracijsko područje se često pretvara u y-pogrešno ili x- netačno (vidi prethodni odlomak). Zatim je potrebno podijeliti područje integracije na dijelove i svaki odgovarajući iterovani integral riješiti zasebno.

Budući da podjela područja integracije na dijelove predstavlja određene poteškoće za mnoge studente, nećemo se ograničiti na primjer naveden u prethodnom paragrafu, već ćemo razmotriti još par primjera.

Primjer 9. Promijenite redoslijed integracije za re-integral

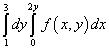Rešenje. Dakle, područje integracije ovog ponovljenog integrala omeđeno je pravim linijama y = 1 , y = 3 , x = 0 , x = 2y .

Kada se integriraju različitim redoslijedom, donja granica regije sastoji se od dvije ravne linije: AB i Pne koje su date jednačinama y= 1 i y = x/ 2, što se može vidjeti na donjoj slici.

Izlaz iz ove neizvjesnosti je podijeliti integracijsko područje na dva dijela. Područje integracije bit će podijeljeno pravom linijom BM... Nove granice integracije izračunavamo pronalaskom inverzne funkcije. Prema ovom rješenju, ponovljeni integral nakon promjene redoslijeda integracije bit će jednak zbroju dva integrala:

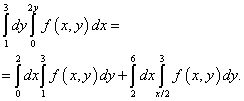
Naravno, isto će biti rješenje dvostrukog integrala, koje se svodi na ponovljeni integral dan u uvjetima ovog primjera.

Primjer 10. Promijenite redoslijed integracije za re-integral

Rešenje. Dakle, područje integracije ponavljanog integrala omeđeno je pravim linijama x = 0 , x= 2 i krive i.

Kao što se vidi na donjoj slici, ravna linija paralelna s osi 0x, preći će donju granicu područja integracije u više od dvije točke.

Stoga ćemo područje integracije podijeliti na tri dijela ravnim linijama koje su na slici crnom bojom. Nove granice integracije izračunavamo pronalaskom inverzne funkcije. Ograničenja za tri nova područja integracije bit će sljedeća.

Prema ovom rješenju, ponovljeni integral nakon promjene redoslijeda integracije bit će jednak zbroju tri integrala:

Isti zbroj tri integrala bit će jednak dvostrukom integralu, što se svodi na ponovljeni integral dan u uvjetu ovog primjera.

Pa ipak, okolnosti više sile često ometaju studente već na prethodnom koraku - postavljanju granica integracije. Anksioznost i konfuzija nisu bez nekog razloga: ako je obično dovoljno pogledati crtež da se regija integracije razbije na dijelove i riješiti ponovljeni integral - tablica integrala, tada je potrebno određeno iskustvo u obuci za postavljanje granica integracije . Prođimo kroz primjer u kojem ćemo se usredotočiti samo na raspored granica integracije i, gotovo automatski, na podjelu domene i izostaviti samo rješenje.

Primjer 11. Pronađite granice integracije dvostrukog integrala ako je područje integracije D postavlja se na sljedeći način:

y - 2x ≤ 0;
2g - x ≥ 0;
xy ≤ 2.

Rešenje. Eksplicitno (kroz x i y"bez nečistoća"), linije koje ograničavaju područje integracije nisu navedene. Budući da za x najčešće ispadaju ravne linije koje u jednom trenutku dodiruju gornje i donje granice izražene kroz igru, tada ćemo ići upravo ovim putem. Štaviše, promjenom redoslijeda integracije dobijamo integracijsko područje sa istim područjem. Riješimo nejednakosti u odnosu na igru i dobijemo:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

Rezultirajuće linije gradimo na crtežu. Ograničenja x-integracije su zaista linije x= 0 i x= 2. Ali pokazalo se da je područje integracije takvo y-pogrešno, jer se gornja granica ne može postaviti jednom linijom y = y(x) .

Preuzmite iz Depositfiles

Predavanja 5-6

Tema2. Više integrala.

Dvostruki integral.

Kontrolna pitanja.

1. Dvostruki integral, njegovo geometrijsko i fizičko značenje

2. Svojstva dvostrukog integrala.

3. Proračun dvostrukog integrala u kartezijanskim koordinatama.

4. Promjena varijabli u dvostrukom integralu. Proračun dvostrukog integrala u polarnim koordinatama.

Neka funkcija z = f (x , y) definirano je u ograničenom zatvorenom području D avion. Hajde da razbijemo područje D proizvoljno uključeno n elementarno zatvorene regije  1 , … , n sa površinama   1 , …,   n i prečnika d 1 , …, d n respektivno. Označavamo d najveći promjer regija  1 , … ,  n... U svakom području  k odaberite proizvoljnu tačku P k (x k , y k) i komponujte integralni zbir funkciju f(x, y)

S =
(1)

Definicija. Dvostruki integral funkciju f(x, y) po površini D naziva se granica integralnog zbira

, (2)

ako postoji.

Komentar. Integralna suma S zavisi od toga kako je regija podijeljena D i izbor tačaka P k (k=1, …, n). Međutim, granica
, ako postoji, ne ovisi o načinu particioniranja regije D i izbor tačaka P k .

Dovoljan uvjet za postojanje dvostrukog integrala. Dvostruki integral (1) postoji ako je funkcija f(x, y) kontinuirano u D osim konačnog broja glatkih krivulja po komadu i ograničeno je na D... U nastavku ćemo pretpostaviti da postoje svi dvostruki integrali koji se razmatraju.

Geometrijsko značenje dvostrukog integrala.

Ako f(x, y) ≥0 u području D, tada je dvostruki integral (1) jednak volumenu "cilindričnog" tijela prikazanog na slici:

V =
(3)

Cilindrično tijelo omeđeno je odozdo područjem D, odozgo  dio površine z = f (x , y), sa strana  vertikalnim segmentima koji povezuju granice ove površine i regije D.

Fizičko značenje dvostrukog integrala. Masa ravne ploče.

Neka je data ravna ploča D s poznatom funkcijom gustoće γ ( NS,at), a zatim podijelite ploču D na dijelove D i i odabirom proizvoljnih tačaka
, dobivamo za masu ploče
, ili, u usporedbi s formulom (2):

(4)

4. Neka svojstva dvostrukog integrala.

Linearnost. Ako WITH Onda je numerička konstanta

Aditivnost. Ako područje D "Podijelite" na područja D 1 i D 2, dakle

3) Područje ograničenog područja D jednak je

(5)

Proračun dvostrukog integrala u kartezijanskim koordinatama.

Neka se navede regija

Slika 1

D = { (x , y ): a ≤ x ≤ b , φ 1 (x ) ≤ y≤ φ 2 (x ) } (6)

Region D zatvoreno u traku između ravnih linija x = a , y = b, odozdo i odozgo omeđen je krivinama y = φ 1 (x ) i y = φ 2 (x ) .

Dvostruki integral (1) po površini D(4) se izračunava prelaskom na ponovljeni integral:

(7)

Ovaj ponovljeni integral izračunava se na sljedeći način. Prvo se izračunava interni integral

po varijabli y, pri čemu x se smatra konstantnim. Rezultat je funkcija varijable x, a zatim se izračunava "vanjski" integral ove funkcije s obzirom na varijablu x .

Komentar. Proces prelaska na ponovljeni integral prema formuli (7) često se naziva raspored granica integracije u dvostrukom integralu. Prilikom postavljanja granica integracije treba imati na umu dvije stvari. Prvo, donja granica integracije ne smije prelaziti gornju, i drugo, granice vanjskog integrala trebaju biti konstantne, a unutrašnji integral općenito ovisiti o varijabli integracije vanjskog integrala.

Sada pustite region D ima formu

D = { (x , y ) : c ≤ y ≤ d , ψ 1 (y ) ≤ x ≤ ψ 2 (y ) } . (8)

Onda

. (9)

Pretpostavimo da je područje D mogu biti predstavljene u obliku (6) i (8) istovremeno. Zatim jednakost

(10)

Prijelaz iz jednog ponovljenog integrala u drugi u jednakosti (10) naziva se promenom redosleda integracije u dvostrukom integralu.

Primjeri.

1) Promijenite redoslijed integracije u integral

Rešenje. Iz oblika ponovljenog integrala nalazimo regiju

D = { (x , y ): 0 ≤ x ≤ 1, 2 x ≤ y≤ 2 } .

Nacrtajmo područje D... Sa slike vidimo da se ovo područje nalazi u vodoravnoj traci između ravnih linija y =0, y= 2 i između redova x =0 i x= D

Ponekad se varijable mijenjaju radi pojednostavljenja izračuna:

,
(11)

Ako su funkcije (11) kontinuirano diferencijabilne, a odrednica (jakobijanska) nije nula u razmatranoj oblasti:

(12)

Ministarstvo obrazovanja i nauke Ruske Federacije

Rad na kursu

Disciplina: Viša matematika

(Osnovno linearno programiranje)

Na temu: VIŠE INTEGRALA

Završeno: ______________

Učitelj: ___________

Datum ___________________

Ocjena _________________

Potpis ________________

VORONEZH 2008

1 Višestruki integrali

1.1 Dvostruki integral

1.2 Trostruki integral

1.3 Više integrala u krivolinijskim koordinatama

1.4 Geometrijske i fizičke primjene više integrala

2 Krivolinijski i površinski integrali

2.1 Krivolinijski integrali

2.2 Površinski integrali

2.3 Geometrijske i fizičke aplikacije

Bibliografija

1 Višestruki integrali

1.1 Dvostruki integral

Zamislimo u Oxy ravnini zatvoreno područje D omeđeno pravom L. Podijelimo ovo područje nekim linijama na n dijelova

, a odgovarajuće najveće udaljenosti između točaka u svakom od ovih dijelova bit će označene sa d 1, d 2, ..., d n. Odaberimo tačku R i u svakom dijelu.

Neka je funkcija z = f (x, y) zadana u području D. Označimo s f (P 1), f (P 2),…, f (P n) vrijednosti ove funkcije na odabranim točkama i sastavimo zbir proizvoda oblika f (P i) ΔS i :

, (1)

zove integralni zbroj za funkciju f (x, y) u domeni D.

Ako postoji ista granica integralnih suma (1) za

i, koji ne ovisi niti o načinu dijeljenja domene D na dijelove, niti o izboru točaka P i u njima, tada se naziva dvostruki integral funkcije f (x, y) nad domenom D i se označava

. (2)

Proračun dvostrukog integrala po površini D omeđenoj pravcima

x = a, x = b (a< b), где φ 1 (х) и φ 2 (х) непрерывны на (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:

(3)

1.2 Trostruki integral

Koncept trostrukog integrala uveden je analogno dvostrukom integralu.

Neka je u prostoru dana neka domena V omeđena zatvorenom površinom S. Definirajmo kontinuiranu funkciju f (x, y, z) u ovoj zatvorenoj domeni. Zatim dijelimo područje V na proizvoljne dijelove Δv i, pretpostavljajući da je volumen svakog dijela jednak Δv i, i sastavljamo integralni zbir oblika

, (4)

Ograničite na

integralne sume (11), koje ne zavise od načina podjele domene V i izbora tačaka P i u svakoj poddomeni ove domene, nazivamo trostrukim integralom funkcije f (x, y, z) nad domena V:

. (5)

Trostruki integral funkcije f (x, y, z) na području V jednak je trostrukom integralu na istom području:

. (6)

1.3 Više integrala u krivolinijskim koordinatama

Uvedimo krivolinijske koordinate na ravnini, nazvane polarne koordinate. Odaberemo točku O (pol) i zrak koji iz nje izlazi (polarna os).

Pirinač. Slika 2 3

Koordinate tačke M (slika 2) će biti dužina MO segmenta - polarni poluprečnik ρ i ugao φ između MO i polarne ose: M (ρ, φ). Imajte na umu da će se za sve točke ravnine, osim za pol, ρ> 0 i polarni kut φ smatrati pozitivnim ako se mjeri u smjeru suprotnom od kazaljke na satu i negativnim kada se mjeri u suprotnom smjeru.

Odnos između polarnih i kartezijanskih koordinata tačke M može se postaviti usklađivanjem ishodišta kartezijanskog koordinatnog sistema sa polom, a pozitivne poluosi Ox - sa polarnom osom (slika 3). Tada je x = ρcosφ, u = ρsinφ. Odavde

, tg.

U domenu D omeđenom krivuljama ρ = Φ 1 (φ) i ρ = Φ 2 (φ), gdje je φ 1< φ < φ 2 , непрерывную функцию z = f(φ, ρ) (рис. 4).

(7)

U trodimenzionalni prostor unose se cilindrične i sferne koordinate.

Cilindrične koordinate tačke P (ρ, φ, z) su polarne koordinate ρ, φ projekcije ove tačke na Oxy ravninu i aplikant ove tačke z (slika 5).

Slika 5 Slika 6

Formule za prijelaz iz cilindričnih koordinata u kartezijanske koordinate mogu se specificirati na sljedeći način:

x = ρcosφ, y = ρsinφ, z = z. (osam)

U sfernim koordinatama položaj tačke u prostoru određen je linearnom koordinatom r - rastojanjem od tačke do ishodišta kartezijanskog koordinatnog sistema (ili pola sfernog sistema), φ - polarnim uglom između pozitivnog poluosi Ox i projekciji točke na ravninu Oxy, a θ - kut između pozitivne poluosi osi Oz i segmenta OP (slika 6). Pri čemu

Postavimo formule za prijelaz sa sfernih koordinata na kartezijanske koordinate:

x = rsinθcosφ, y = rsinθsinφ, z = rcosθ. (devet)

Tada će formule za prijelaz na cilindrične ili sferne koordinate u trostrukom integralu izgledati ovako: