محاضرات تكاملات متعددة ، تكامل مزدوج. حساب التكاملات المزدوجة: النظرية والأمثلة حل التكاملات المتعددة

ديف . اسمحوا ان ،
,

.

المجموعة تسمى فجوة مغلقة أو شريط مغلق في .

المجموعة تسمى فجوة مفتوحة

أو شريط مفتوح في .

ديف . قياس الفترات و الكمية تسمى:

(أكثر دقة
).

ديف . لو
مثل ذلك
ثم الفاصل الزمني يسمى المنحل و
.

خصائص قياس التباعد:

أ). الإيجابية:
، و
إذا وفقط إذا - متدهور.

ب). التوحيد الإيجابي:.

الخامس). إضافة:

* ل
مثل ذلك
;

* ل
و

.

ز). رتابة القياس:.

ديف . قطر العارضة (الفجوة) هي القيمة:

لاحظ أن
و
ليسوا نفس الشيء. على سبيل المثال ، إذا - تتدهور إذن
، أ
(بشكل عام).

حيث: * ؛

* ;*
.

ديف . الإجمال
تباعد فرعي يسمى تقسيم الفترة ، لو: *؛

*
; *
; *
; *
.

الكمية
يسمى معلمة القسم ص(حيث
).

ديف . شق يسمى صقل القسم إذا كانت جميع عناصر القسم تم الحصول عليها عن طريق تقسيم العناصر المنقسمة .

يشار إلى:
... يقرأ: الأصغر أو أكبر .

بالنسبة للعلاقة الأكبر والأصغر ، هذا صحيح:

*. عبورية -؛ *.
;

*.

; *.

|
.

§. تعريف التكامل المتعدد

اسمحوا ان
- الأخشاب (فجوة) في ,
- تقسيم الفجوة أنا... في كل فترات من القسم حدد النقطة
.

نحن نحصل
انقسم بنقاط ملحوظة لـ
.

الكمية
يسمى مجموع ريمان المتكامل للوظيفة F (x) في الفترة الفاصلة أنا بالتقسيم بنقاط محددة
.

ديف :
=
=
.

دلالة - مجموعة وظائف تكاملية على شريط أنا نكتب:

ديف : ε > 0 δ>0<.

إذا كان للوظيفة F(x) تشغيل أناوالانقسام
- للدلالة به
- أكبر وأصغر قيمة للدالة F(x) تشغيل أنا كثم الكميات
=
و
=
تسمى مجموع داربوكس السفلي والعلوي.

§. معيار Darboux لوجود تكامل متعدد.

تي 0 . لتعمل
كان قابلًا للتكامل على شريط (أولئك.
) ضروري وكافي أن

. Δ▲.

تم تحديد تكامل الوظيفة على شريط في الفضاء الإقليدي. كيفية تكامل الوظيفة على مجموعة محدودة من الفضاء الإقليدي؟

دعونا نحدد تكامل الوظيفة F بالمجموعة
.

ديف : اسمحوا ان
و
- محدودة ، أي
... وظيفة
تسمى الوظيفة المميزة للمجموعة م.

ثم:
≡
.

لا يعتمد تعريف التكامل على مجموعة على الشريط الذي يحتوي على مالمختار ، أي

.

هذا يعني أن تعريف التكامل على مجموعة صحيح.

شرط ضروري للتكامل.لتعمل F(x) تشغيل متكون قابلة للتكامل ، فمن الضروري أن F(x) كان يقتصر على م. Δ▲.

§. خصائص التكاملات المتعددة.

1  . الخطية: كثير ص موظائف تكامل على المجموعة م -خطي

الفضاء و
- وظيفية خطية.

2  . حالة التطبيع:
... شكل آخر من أشكال التدوين
في الواقع يحدد مقياس مجموعة عشوائية من الفضاء الإقليدي.

3  . إذا كان التكامل على مجموعة من Lebesgue يقيس الصفر ، فهو موجود

هو صفر.

ملحوظة:الكثير من متسمى مجموعة ليبيسج قياس الصفر ،

لو

مثل ذلك
و
.

4  . أ.;ب.;

الخامس.لو
و - مفصولة عن الصفر بـ م، من ثم

5  .
و F=زالكمبيوتر. (في كل مكان تقريبًا) م، من ثم
.

6  . الجمع: إذا
و
من ثم

بشكل عام:
.

Δ. يتبع من المساواة: ▲

7  . روتيني:
و
من ثم
.

8  . تكامل عدم المساواة: إذا
إيتو

9  . اسمحوا ان

... إلى
، من الضروري والكافي وجود نقطة داخلية للمجموعة م، حيث F (x)> 0 وهو مستمر.

10  . تكامل وحدة الوظيفة التي يتم دمجها:
.

11  . نظرية المتوسط:
,
تشغيل ميحافظ على العلامة و
، من ثم

إذا كانت المجموعة م- متصل و F(x) مستمر في
من ثم
مثل ذلك
.

12  . لكي يكون تكامل الدالة غير السالبة مساويًا للصفر

ضرورية وكافية ل F(x) = 0 في كل مكان تقريبًا م.

13  . نظرية فوبيني.للتكامل المزدوج:

دع المنطقة
- مستطيل:. بعد ذلك ، في حالة وجود تكاملات مفردة داخلية ، للعثور على التكامل المزدوج ، يمكن للمرء المضي قدمًا في التكامل المتكرر (انظر الشكل أ):

، أو

إذا لم يكن مجال التكامل مستطيلاً ، فإن نظرية فوبيني لا تزال صالحة ولها الشكل (انظر الشكل ب):

. (*)

ملحوظة:يجب أن تكون الحدود الخارجية للتكامل ثوابت ، وقد تعتمد الحدود الداخلية للتكامل على المتغير الذي لا يزال يتعين إجراء التكامل عليه.

يمكن الحصول على الصيغة (*) باستخدام الوظيفة المميزة للمجموعة د.

للتكامل المتعدد:

دع بعض المجموعات الفرعية من المساحات الإقليدية و ... نحدد المنتج الديكارتي لهذه المجموعات ، وهو مجموعة فرعية من الفضاء الإقليدي
:.

ثم نظرية Fubini ل
يشبه:
.

النظرية صالحة أيضًا للأشرطة Xو صوللتكوينات الأكثر تعقيدًا.

أمثلة:

1 0 . احسب
إذا كانت حدود المنطقة
المعطاة من المعادلات:

... بإيجاد نقاط تقاطع المنحنيات التي تحدد حدود المنطقة ، نحصل على نقطتين:

... ثم الترتيب المحتمل لحدود التكامل عند المرور إلى التكاملات المتكررة يعطي:

أ).
;

0 . قم بتغيير ترتيب التكامل في إعادة التكامل:

–

وصفة:عند تعيين حدود التكامل في تكامل مزدوج ، يوصى بالبدء بالحدود الخارجية للتكامل.

0 . احسب:

، لو

يمنح التمرير إلى التكاملات المتكررة:
.

في هذه الحالة ، في التكامل الثلاثي ، يجب أن يبدأ ترتيب الحدود بالحدود الداخلية للتكامل. ثم قم بتخطيط المنطقة الخامسعلى متن الطائرة xOy

وضع حدود في المنطقة د- الكذب في الطائرة xOy.

4 0 . قم بتغيير ترتيب التكامل في إعادة التكامل:
.

دعونا نتناول المزيد من التفاصيل إلى حد ما حول أعمال Ostrogradskii على التكاملات المتعددة.

صيغة Ostrogradsky لتحويل تكامل ثلاثي إلى تكامل مزدوج ، والتي نكتبها عادة في الصورة

حيث div A هو تباعد مجال المتجه A ،

A هو الناتج القياسي للمتجه A بواسطة متجه الوحدة للخط الطبيعي الخارجي n لسطح الحدود ؛ في الأدبيات الرياضية غالبًا ما كان مرتبطًا سابقًا بأسماء Gauss و Green.

في الواقع ، في عمل Gauss على جذب الأجسام الشبه الكروية ، يمكن للمرء أن يرى فقط حالات خاصة جدًا من الصيغة (1) ، على سبيل المثال ، لـ P = x ، Q = R = 0 ، إلخ. أما بالنسبة لـ J. Green ، في عمله على نظرية الكهرباء ولا توجد مغناطيسية للصيغة (1) على الإطلاق ؛ استنتجت علاقة أخرى بين التكاملات الثلاثية والمزدوجة ، وهي صيغة جرين لمشغل لابلاس ، والتي يمكن كتابتها في النموذج

بالطبع ، يمكن استخلاص الصيغة (1) من (2) عن طريق الإعداد

وبنفس الطريقة يمكنك الحصول على الصيغة (2) من الصيغة (1) ، لكن جرين لم يفكر حتى في القيام بذلك.

حيث يكون التكامل فوق الحجم على اليسار ، والتكامل الموجود على سطح الحد على اليمين ، وهذه هي اتجاه جيب التمام الخارجي.

تشهد المخطوطات الباريسية لأوستروجرادسكي ، بيقين كامل ، أن كلا من الاكتشاف والتواصل الأول لنظرية التكامل (1) كان يخصه. لأول مرة تم التعبير عنها وإثباتها ، تمامًا كما يحدث الآن في "إثبات نظرية التفاضل والتكامل" المقدم إلى أكاديمية باريس للعلوم في 13 فبراير 1826 ، وبعد ذلك تمت صياغته مرة أخرى في ذلك الجزء من "مذكرات عن انتشار الحرارة في الداخل المواد الصلبة"، الذي قدمه أوستروجرادسكي في 6 أغسطس 1827. أعطيت" مذكرات "إلى فورييه وبواسون لمراجعتها ، وقد قرأها الأخير بالتأكيد ، كما يتضح من المدخل على الصفحات الأولى من كلا الجزأين من المخطوطة. بالطبع ، لم يفكر بواسون حتى في أن ينسب إلى نفسه النظرية التي التقى بها في أعمال أوستروجرادسكي قبل عامين من تقديم عمله حول نظرية المرونة.

بالنسبة للعلاقة بين الأعمال المتعلقة بالتكاملات المتعددة لأوستروجرادسكي والأخضر ، نتذكر أنه في "ملاحظة حول نظرية الحرارة" تم اشتقاق صيغة تتضمن صيغة جرين الخاصة ، كحالة خاصة جدًا. رمزية كوشي غير المعتادة الآن ، التي استخدمها أوستروجرادسكي في "الملاحظة" ، أخفت حتى وقت قريب هذا الاكتشاف المهم عن الباحثين. بالطبع ، يحتفظ جرين بشرف الاكتشاف والنشر الأول في عام 1828 لصيغة مشغلي لابلاس التي تحمل اسمه.

ساعد اكتشاف صيغة تحويل التكامل الثلاثي إلى تكامل مزدوج Ostrogradskii في حل مشكلة تغيير تكامل n-fold ، أي اشتقاق الصيغة العامة لتحويل تكامل تعبير من نوع الاختلاف. على المجال ذو البعد n والتكامل على السطح الفائق المحيط S مع المعادلة L (x ، y ، z ، ...) = 0. إذا التزمنا بالتدوين السابق ، فسيكون للصيغة الشكل

ومع ذلك ، لم يستخدم Ostrogradsky الصور والمصطلحات الهندسية التي نستخدمها: هندسة الفضاءات متعددة الأبعاد لم تكن موجودة بعد في ذلك الوقت.

في مذكرات حساب التفاضل والتكامل في التكاملات المتعددة ، تم النظر في سؤالين أكثر أهمية حول نظرية مثل هذه التكاملات. أولاً ، يستنتج أوستروجرادسكي صيغة لتغيير المتغيرات في تكامل متعدد الأبعاد ؛ ثانيًا ، لأول مرة يقدم وصفًا كاملاً ودقيقًا لطريقة حساب تكامل n-fold باستخدام n تكاملات متتالية على كل من المتغيرات ضمن الحدود المناسبة. أخيرًا ، من الصيغ الواردة في هذه المذكرات ، من السهل الاستنتاج قاعدة عامةالتمايز فيما يتعلق بمعامل التكامل متعدد الأبعاد ، عندما لا يعتمد هذا المعامل على هذا المعامل فحسب ، بل يعتمد أيضًا على حدود منطقة التكامل. تأتي هذه القاعدة من الصيغ الموجودة في المذكرات بطريقة طبيعية لدرجة أن علماء الرياضيات في وقت لاحق حددوها بإحدى صيغ هذه المذكرات.

كرس Ostrogradskii عملاً خاصًا لتغيير المتغيرات في تكاملات متعددة. بالنسبة للتكامل المزدوج ، تم اشتقاق القاعدة المقابلة باستخدام التحويلات الشكلية بواسطة أويلر ، للتكامل الثلاثي ، بواسطة لاغرانج. ومع ذلك ، على الرغم من أن نتيجة لاجرانج صحيحة ، إلا أن منطقه لم يكن دقيقًا: بدا أنه ينطلق من حقيقة أن عناصر الحجم في المتغيرات القديمة والجديدة - الإحداثيات - متساوية مع بعضها البعض. ارتكب Ostrogradskii خطأً مماثلاً في البداية في الاشتقاق المذكور للتو لقاعدة تغيير المتغيرات. في مقال "حول تحويل المتغيرات في تكاملات متعددة" ، كشف أوستروجرادسكي عن خطأ لاغرانج ، وقدم أيضًا لأول مرة طريقة هندسية واضحة لتحويل المتغيرات في تكامل مزدوج ، والتي ، في شكل أكثر صرامة إلى حد ما ، تم تقديمها أيضًا في كتيباتنا. وبالتحديد ، عند تغيير المتغيرات في التكامل وفقًا للصيغ ، يتم تقسيم منطقة التكامل على خطوط إحداثيات النظامين u = const ، v = const إلى رباعي الزوايا منحنية متناهية الصغر. ثم يمكن الحصول على التكامل من خلال جمع عناصره أولاً التي تتوافق مع شريط منحني ضيق بلا حدود ، ثم الاستمرار في جمع العناصر بالشرائح حتى يتم استنفادها جميعًا. تعطي عملية حسابية بسيطة للمنطقة ، والتي يمكن اعتبارها متوازي أضلاع حتى ترتيب أعلى صغير ، يتم اختيار التعبير ، حيث ، بحيث تكون المنطقة موجبة. نتيجة لذلك ، نحصل على الصيغة المعروفة

لدالة من متغيرين معرّفين كـ ض = F(x, ذ) .

التكامل المزدوج مكتوب على النحو التالي:

هنا د- شكل مسطح محاط بخطوط ، يتم إعطاء تعبيرات (المساواة) في مهمة حساب التكامل المزدوج. اليسار واليمين - المساواة التي يكون فيها المتغير على اليسار x، وفوق وتحت - المساواة التي يكون فيها المتغير الموجود على اليسار ذ... هذا المكان وما بعده - أحد أهم الأشياء لفهم تقنية حساب التكامل المزدوج.

احسب التكامل المزدوج - يعني إيجاد رقم مساوٍ لمساحة الشكل المذكور د .

حتى نلمس تعريفات التكامل المزدوج ، لكننا سنتعلم حسابها. من الأسهل فهم معنى التكامل المزدوج عندما تحل عدة مسائل لحسابها ، لذلك ستجد تعريف التكامل المزدوج في نهاية هذا الدرس. بالمضي قدمًا قليلاً ، يمكننا فقط ملاحظة أن تعريف التكامل المزدوج يرتبط أيضًا بالشكل المذكور أعلاه د .

إذا كان الرقم دمستطيل ، كل الخطوط المحيطة به هي خطوط مستقيمة. إذا كان الرقم د- منحني الخطي ، ثم على اليسار وعلى اليمين يتم تحديده بخطوط مستقيمة ، وفوق وأسفل - بخطوط منحنية ناتجة عن المساواة الواردة في المهمة. هناك أوقات عندما يكون الرقم د- مثلث ، ولكن عن مثل هذه الحالات قليلاً.

لحساب التكامل المزدوج ، من الضروري ، بالتالي ، فرز الخطوط المتاخمة للشكل دالتي لها اسم صارم - مجال التكامل. فرز إلى اليسار واليمين والأعلى والأسفل. سيكون هذا مطلوبًا عندما تقليل التكامل المزدوج للتكامل المتكرر - طريقة حساب التكامل المزدوج.

حالة منطقة مستطيلة:

حالة المنطقة المنحنية:

وهذا هو بالفعل حل بعض التكاملات المألوفة لدينا ، حيث يتم إعطاء الحدين العلوي والسفلي للتكامل. التعبيرات التي تحدد الخطوط التي تربط الشكل د، ستكون حدود التكامل للتكاملات المحددة العادية ، والتي اقتربنا منها بالفعل.

اختزال تكامل مزدوج إلى تكامل متكرر

حالة منطقة مستطيلة

دع هذه الوظيفة لها تكامل مزدوج

إلى احسب هذا التكامل المزدوج ، من الضروري اختزاله إلى تكامل متكرر له الشكل

تحتاج أولاً إلى حساب التكامل المحدد الداخلي (الأيمن) ، ثم - التكامل الخارجي المحدد (الأيسر).

يمكنك تغيير الأدوار xو ذ

مثال 1.احسب التكامل المزدوج

نحسب التكامل الداخلي (الأيمن) ، بافتراض أن y ثابت. استلمنا.

مثال 2.احسب التكامل المزدوج

حل. اختزل هذا التكامل المزدوج للتكامل المتكرر

في الرسم نبني منطقة التكامل:

الآن نحسب التكامل الخارجي (الأيسر) للتكامل الداخلي (الأيمن) المحسوب للتو:

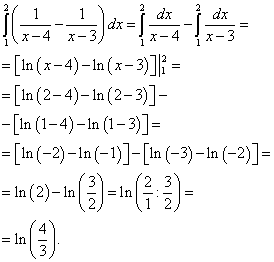
ستكون النتيجة هي حل هذا التكامل المزدوج.

احسب التكامل المزدوج بنفسك ثم انظر إلى الحل

حالة المنطقة المنحنية أو المثلثة

دعنا نعطي مرة أخرى دالة من متغيرين F(x, ذ) والقيود الخاصة بـ د: بالفعل من نوع مختلف قليلاً:

هذا الدخول يعني أن الرقم دالحد الأيسر والأيمن ، كما في حالة المنطقة المستقيمة - الخطوط المستقيمة x = أو x = ب، ولكن أسفل وما فوق منحنيات معطاة بواسطة المعادلات و. وبعبارة أخرى ، هي وظائف.

دع هذه الوظيفة لها أيضًا تكامل مزدوج

لحساب هذا التكامل المزدوج ، من الضروري اختزاله إلى تكامل متكرر له الشكل

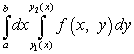هنا حدود التكامل أو بهي أرقام ، وهي وظائف. في حالة منطقة مثلثية ، إحدى وظائف أو هي معادلة الخط المستقيم. سيتم تحليل هذه الحالة في المثال 3.

كما في حالة المنطقة المستقيمة ، تحتاج أولاً إلى حساب التكامل الصحيح المحدد ، ثم التكامل المحدد الأيسر.

وبالمثل ، يمكنك تبادل الأدوار xو ذ... ثم التكامل المتكرر سيكون له الشكل

يجب حل هذا التكامل المتكرر بنفس الطريقة: أولاً ، التكامل الداخلي (الأيمن) ، ثم التكامل الخارجي (الأيسر).

مثال 5.احسب التكامل المزدوج

حل. اختزل هذا التكامل المزدوج للتكامل المتكرر

في الرسم نقوم ببناء منطقة التكامل ونرى أنها مثلثية:

نحسب التكامل الداخلي (الأيمن) باعتبار x ثابتًا. استلمنا.

الآن نحسب التكامل الخارجي (الأيسر) للتكامل الداخلي (الأيمن) المحسوب للتو. أولاً ، نمثل هذا التكامل كمجموع التكاملات:

نحسب المصطلح الأول:

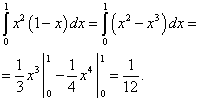
نحسب المصطلح الثاني:

نحسب المصطلح الثالث:

نحصل على المجموع ، والذي سيكون الحل لهذا التكامل المزدوج:

مثال 6.احسب التكامل المزدوج

حل. اختزل هذا التكامل المزدوج للتكامل المتكرر

في الرسم نبني منطقة التكامل:

نحسب التكامل الداخلي (الأيمن) باعتبار x ثابتًا. استلمنا.

الآن نحسب التكامل الخارجي (الأيسر) للتكامل الداخلي (الأيمن) المحسوب للتو:

ستكون النتيجة هي حل هذا التكامل المزدوج.

x- صحيح وغير صحيح ، ذ- مجالات التكامل الصحيحة وغير الصحيحة

يحدث أن تكون منطقة تكامل التكامل المزدوج محدودة بهذه الخطوط بحيث يصبح من الضروري تقسيم منطقة التكامل إلى أجزاء وحل كل تكامل متكرر متطابق بشكل منفصل. هذه هي الحالات عندما:

1) منطقة التكامل عبارة عن شكل به خطان أو أكثر من الخطوط المستقيمة أو المنحنية على شكل حد سفلي أو علوي (يسار أو يمين) ؛

2) منطقة التكامل هي شكل تتقاطع حدوده الخطوط المستقيمة عند أكثر من نقطتين.

إذا كان ما سبق ينطبق على الحد الأيسر أو الأيمن من منطقة التكامل ، أي القيود التي تحددها الخطوط المعبر عنها من حيث x، ثم تسمى منطقة التكامل x-خاطئ. إذا كان مستقيم ذ = ذ0 يتقاطع مع الحدود المقابلة عند نقطة واحدة فقط ، وإذا كان هناك خط مستقيم أو منحنى واحد فقط يعمل كحدود ، فإن منطقة التكامل تسمى x- صيح

وبالمثل ، إذا تم تحديد الحدود بواسطة الخطوط التي يتم التعبير عنها من خلالها ذ، مباشرة x = x0 يتقاطع عند أكثر من نقطة واحدة أو إذا كان هناك أكثر من خط مستقيم أو منحنى يعمل كحدود ، فإن منطقة التكامل تسمى ذ-خاطئ. اعرض اللافتات الآن ذ-من المفترض أن تكون المنطقة الصحيحة بسيطة للغاية.

حتى الآن ، نظرنا في أمثلة مع x- غير صحيح و ذ- مجالات التكامل الصحيحة. الآن دعونا ننظر في الحالات التي يتم فيها انتهاك شرط الصواب.

مثال 7.احسب التكامل المزدوج ، حيث تحد مساحة تكامله بخطوط ذ = x , س ص = 1 , ذ = 2 .

حل. مجال التكامل هو ذ-خطأ ، حيث لا يمكن تعيين حده السفلي بسطر واحد ذ = ذ(x) ... كما ترى في الصورة أعلاه ، يتكون الحد السفلي من ذ = x(بورجوندي غامق) و س ص= 1 (أخضر). لذلك مباشرة x= 1 (أسود) يمكننا تقسيم منطقة التكامل إلى قسمين - و.

يتم حساب هذا التكامل المزدوج على النحو التالي:

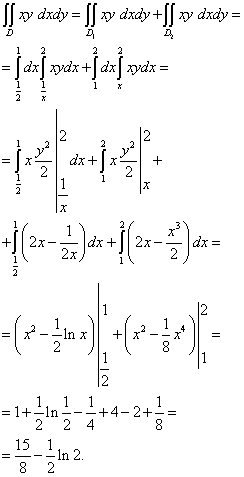
تغيير ترتيب التكامل

كما هو مذكور أعلاه ، بعد تقليل التكامل المزدوج للتكامل المتكرر ، يمكن للمرء تغيير المتغيرات xو ذالأدوار ، أو بعبارة أخرى ، تغيير ترتيب التكامل.

يمكن وصف التغيير في ترتيب التكامل من الناحية المجازية بالكلمات التالية حول "هنري": هكذا يتصرف ساكن في الغابة - وحش ، مرة واحدة في قفص ، وهذه هي الطريقة التي يتصرف بها ساكن قفص - رجل تائه في غابة الشكوك ". ونفس الشيء:" مزق تشالمرز الرسالة إلى ألف قطعة صغيرة وبدأ بتمزيق سجادته باهظة الثمن ، متقدمًا عليها ذهابًا وإيابًا. " ( اوه هنري. شهرزاد ميدان ماديسون.)

ثم ، إذا كان لدينا التكامل الأيسر بالنسبة للمتغير x، والصحيح - بواسطة ذ، فبعد تغيير ترتيب التكامل سيكون كل شيء في الاتجاه المعاكس. ثم يجب "استعارة" حدود التكامل للعبة "الجديدة" من x "القديمة" ، ويجب الحصول على حدود التكامل لـ x "الجديدة" بالشكل وظيفة عكسية، بعد حل معادلة x ، والتي حددت حد اللعبة.

المثال 8.

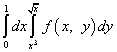حل. بعد تغيير ترتيب التكامل ، يصبح التكامل على اللعبة يسارًا ، ويصبح التكامل على x صحيحًا. سيتم استعارة حدود التكامل للعبة "الجديدة" من x "القديمة" ، أي أن الحد الأدنى يساوي صفرًا والحد الأعلى يساوي واحدًا. حدود التكامل للعبة "القديمة" تعطى بواسطة المعادلات و. بعد حل هذه المعادلات لـ x ، نحصل على حدود جديدة للتكامل لـ x:

(أسفل) و (أعلى).

وبالتالي ، بعد تغيير ترتيب التكامل ، سيتم كتابة التكامل المكرر على النحو التالي:

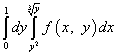بعد تغيير ترتيب التكامل في التكامل المزدوج ، غالبًا ما تتحول منطقة التكامل إلى ذ-خطأ أو x- غير صحيح (راجع الفقرة السابقة). بعد ذلك ، يلزم تقسيم منطقة التكامل إلى أجزاء وحل كل تكامل متكرر مناظر على حدة.

نظرًا لأن تقسيم منطقة التكامل إلى أجزاء يمثل بعض الصعوبات للعديد من الطلاب ، فلن نقتصر على المثال الوارد في الفقرة السابقة ، ولكننا سننظر في بعض الأمثلة الأخرى.

المثال 9.قم بتغيير ترتيب التكامل لإعادة التكامل

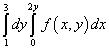حل. إذن ، منطقة تكامل هذا التكامل المتكرر تحدها الخطوط المستقيمة ذ = 1 , ذ = 3 , x = 0 , x = 2ذ .

عند التكامل بترتيب مختلف ، فإن الحد الأدنى للمنطقة يتكون من خطين مستقيمين: ABو قبل الميلادالتي تعطى بواسطة المعادلات ذ= 1 و ذ = x/ 2 ، والتي يمكن رؤيتها في الشكل أدناه.

المخرج من حالة عدم اليقين هذه هو تقسيم منطقة التكامل إلى قسمين. سيتم تقسيم منطقة التكامل بخط مستقيم بي ام... نحسب حدود التكامل الجديدة بإيجاد الدالة العكسية. وفقًا لهذا الحل ، فإن التكامل المتكرر بعد تغيير ترتيب التكامل سيكون مساويًا لمجموع تكاملين:

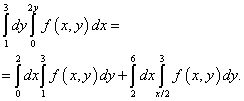
بطبيعة الحال ، سيكون نفس حل التكامل المزدوج ، مما يقلل إلى التكامل المتكرر المعطى في حالة هذا المثال.

المثال 10.قم بتغيير ترتيب التكامل لإعادة التكامل

حل. إذن ، منطقة تكامل التكامل المتكرر تحدها الخطوط المستقيمة x = 0 , x= 2 ومنحنيات و.

كما هو موضح في الصورة أدناه ، خط مستقيم موازٍ للمحور 0x، سوف تعبر الحدود الدنيا لمنطقة التكامل بأكثر من نقطتين.

لذلك ، سنقسم منطقة التكامل إلى ثلاثة أجزاء بخطوط مستقيمة مرسومة باللون الأسود في الشكل. نحسب حدود التكامل الجديدة بإيجاد الدالة العكسية. ستكون حدود مناطق التكامل الثلاثة الجديدة على النحو التالي.

وفقًا لهذا الحل ، فإن التكامل المتكرر بعد تغيير ترتيب التكامل سيكون مساويًا لمجموع ثلاثة تكاملات:

سيكون نفس مجموع ثلاثة تكاملات مساوية للتكامل المزدوج ، مما يقلل إلى التكامل المتكرر المعطى في حالة هذا المثال.

ومع ذلك ، غالبًا ما تتداخل ظروف القوة القاهرة مع الطلاب في الخطوة السابقة بالفعل - تحديد حدود الاندماج. القلق والارتباك ليسا بلا سبب: إذا كان من الكافي عادة النظر إلى الرسم لتقسيم منطقة التكامل إلى أجزاء ، ولحل التكامل المتكرر - جدول التكاملات ، فإن بعض الخبرة التدريبية مطلوبة في تحديد حدود التكامل . دعونا نمر بمثال سنركز فيه فقط على ترتيب حدود التكامل ، وبشكل تلقائي تقريبًا ، على تقسيم المجال ونهمل الحل نفسه.

المثال 11.أوجد حدود تكامل تكامل مزدوج إذا كانت منطقة التكامل دعلى النحو التالي:

ذ - 2x ≤ 0;
2 س - x ≥ 0;
س ص ≤ 2.

حل. صراحة (من خلال xو ذ"بدون شوائب") ، لم يتم تحديد الخطوط المحيطة بمنطقة التكامل. نظرًا لأن x ، غالبًا ما يتحول إلى خطوط مستقيمة ، تلامس في وقت ما الحدود العليا والسفلى ، المعبر عنها من خلال اللعبة ، ثم سنذهب بالضبط على طول هذا المسار. علاوة على ذلك ، عند تغيير ترتيب التكامل ، نحصل على منطقة تكامل بنفس المنطقة. دعونا نحل عدم المساواة فيما يتعلق باللعبة ونحصل على:

ذ ≤ 2x;
ذ ≥ x/2;
ذ ≤ 2/x.

نبني الخطوط الناتجة في الرسم. إن حدود تكامل x هي بالفعل الخطوط x= 0 و x= 2. لكن تحولت منطقة التكامل ذ-خطأ ، حيث لا يمكن تعيين حده العلوي بسطر واحد ذ = ذ(x) .

تنزيل من Depositfiles

محاضرات 5-6

الموضوع 2. تكاملات متعددة.

تكامل مزدوج.

أسئلة التحكم.

1. التكامل المزدوج ، معناه الهندسي والمادي

2. خصائص التكامل المزدوج.

3. حساب التكامل المزدوج في الإحداثيات الديكارتية.

4. تغيير المتغيرات في تكامل مزدوج. حساب التكامل المزدوج في الإحداثيات القطبية.

دع الوظيفة ض = F (x , ذ) في منطقة مغلقة محدودة دطائرة. دعونا نقسم المنطقة دبشكل تعسفي نالمناطق المغلقة الابتدائية  1 , … , نبالمناطق   1 , …,   نوأقطار د 1 , …, د ن على التوالى. نشير دأكبر أقطار المناطق  1 , … ,  ن... في كل منطقة  كاختر نقطة عشوائية ص ك (x ك ، ذ ك) وتأليف مجموع متكاملالمهام F(س ، ص)

س =
(1)

تعريف. تكامل مزدوجالمهام F(س ، ص) حسب المنطقة ديسمى حد المجموع المتكامل

, (2)

إذا كانت موجودة.

تعليق. مبلغ لا يتجزأ سيعتمد على كيفية تقسيم المنطقة دواختيار النقطة ص ك (ك=1, …, ن). ومع ذلك ، فإن الحد
ان وجدت لا تعتمد على طريقة تقسيم المنطقة دواختيار النقطة ص ك .

شرط كاف لوجود تكامل مزدوج. التكامل المزدوج (1) موجود إذا كانت الدالة F(س ، ص) مستمر في دباستثناء عدد محدود من المنحنيات السلسة متعددة التعريفات ويحدها د... فيما يلي ، سنفترض أن جميع التكاملات المزدوجة قيد الدراسة موجودة.

المعنى الهندسي للتكامل المزدوج.

لو F(س ، ص) ≥0 في المنطقة د، ثم التكامل المزدوج (1) يساوي حجم الجسم "الأسطواني" الموضح في الشكل:

الخامس =
(3)

الجسم الأسطواني تحده منطقة من الأسفل د، من أعلى جزء من السطح ض = F (x , ذ) ، من الجوانب - مقاطع الخط العمودي التي تربط حدود هذا السطح والمنطقة د.

المعنى المادي للتكامل المزدوج. كتلة اللوحة المسطحة.

دع طبق مسطح يعطى دمع دالة الكثافة المعروفة γ ( NS ،في) ، ثم تقسيم اللوحة D إلى أجزاء D أناواختيار النقاط العشوائية
، نحصل عليها لكتلة اللوحة
، أو المقارنة مع الصيغة (2):

(4)

4. بعض خصائص التكامل المزدوج.

الخطية.لو معإذن هو ثابت رقمي

الجمع.إذا كانت المنطقة د "انقسام" إلى مناطق د 1 و د 2 ، إذن

3) مساحة محدودة ديساوي

(5)

حساب التكامل المزدوج في الإحداثيات الديكارتية.

دع المنطقة تعطى

الصورة 1

د = { (x , ذ ): أ ≤ س ≤ ب , φ 1 (x ) ≤ أنت φ 2 (x ) } (6)

منطقة د محاطة بشريط بين خطوط مستقيمة x = أ , ذ = ب، من الأسفل ومن الأعلى ، على التوالي ، يحده المنحنيات ذ = φ 1 (x ) و ذ = φ 2 (x ) .

تكامل مزدوج (1) فوق المنطقة د(4) يتم حسابه بالتمرير إلى التكامل المتكرر:

(7)

يتم حساب هذا التكامل المتكرر على النحو التالي. أولاً ، يتم حساب التكامل الداخلي

حسب المتغير ذ، حيث xيعتبر ثابتًا. والنتيجة هي دالة للمتغير x، ثم يتم حساب التكامل "الخارجي" لهذه الدالة فيما يتعلق بالمتغير x .

تعليق. غالبًا ما تسمى عملية الانتقال إلى التكامل المتكرر وفقًا للصيغة (7) ترتيب حدود التكامل في التكامل المزدوج. عند تحديد حدود التكامل ، يجب مراعاة نقطتين. أولاً ، يجب ألا يتجاوز الحد الأدنى للتكامل الحد الأعلى ، وثانيًا ، يجب أن تكون حدود التكامل الخارجي ثابتة ، ويجب أن يعتمد التكامل الداخلي بشكل عام على متغير تكامل التكامل الخارجي.

الآن دع المنطقة دلديه الشكل

د = { (x , ذ ) : ج ≤ ص ≤ د , ψ 1 (ذ ) ≤ س ≤ ψ 2 (ذ ) } . (8)

ثم

. (9)

افترض أن المنطقة ديمكن تمثيلها بالشكل (6) و (8) في آن واحد. ثم المساواة

(10)

يسمى المقطع من واحد مكمل للآخر في المساواة (10) عن طريق تغيير ترتيب التكاملفي التكامل المزدوج.

أمثلة.

1) قم بتغيير ترتيب التكامل في التكامل

حل. من شكل التكامل المتكرر ، نجد المنطقة

د = { (x , ذ ): 0 ≤ س ≤ 1, 2 س ≤ ذ 2 } .

لنرسم المنطقة د... من الشكل ، نرى أن هذه المنطقة تقع في شريط أفقي بين خطوط مستقيمة ذ =0, ذ= 2 وبين السطور x =0 و x= د

في بعض الأحيان يتم تغيير المتغيرات لتبسيط العمليات الحسابية:

,
(11)

إذا كانت الدوال (11) قابلة للتفاضل باستمرار وكان المحدد (Jacobian) غير صفري في المجال المدروس:

(12)

وزارة التربية والتعليم والعلوم في الاتحاد الروسي

عمل الدورة

الانضباط: الرياضيات العليا

(البرمجة الخطية الأساسية)

حول الموضوع: تكاملات متعددة

مكتمل: ______________

معلم:___________

تاريخ ___________________

رتبة _________________

إمضاء ________________

فورونيج 2008

1 تكاملات متعددة

1.1 تكامل مزدوج

1.2 تكامل ثلاثي

1.3 تكاملات متعددة في إحداثيات منحنية الخطوط

1.4 التطبيقات الهندسية والفيزيائية للتكاملات المتعددة

2 التكاملات المنحنية والسطحية

2.1 التكاملات المنحنية

2.2 تكاملات السطح

2.3 التطبيقات الهندسية والفيزيائية

فهرس

1 تكاملات متعددة

1.1 تكامل مزدوج

ضع في اعتبارك في مستوى Oxy منطقة مغلقة D يحدها خط L. نقسم هذه المنطقة ببعض الخطوط إلى أجزاء n

، والمسافات الأكبر المقابلة بين النقاط في كل جزء من هذه الأجزاء سيتم الإشارة إليها بـ d 1 ، d 2 ، ... ، d n. دعنا نختار النقطة Р i في كل جزء.

دع الدالة z = f (x، y) تعطى في المجال D. دعونا نشير بواسطة f (P 1) ، f (P 2) ، ... ، f (P n) قيم هذه الوظيفة عند النقاط المحددة ونؤلف مجموع المنتجات بالشكل f (P i) ΔS i :

, (1)

يسمى المجموع المتكامل للدالة f (x ، y) في المجال D.

في حالة وجود نفس الحد من المبالغ المتكاملة (1) لـ

والتي لا تعتمد إما على طريقة تقسيم المجال D إلى أجزاء ، أو على اختيار النقاط P i فيها ، ثم يطلق عليها التكامل المزدوج للوظيفة f (x ، y) على المجال D و يشار إليه

. (2)

حساب التكامل المزدوج على المنطقة D المحاطة بخطوط

س = أ ، س = ب (أ< b), где φ 1 (х) и φ 2 (х) непрерывны на (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:

(3)

1.2 تكامل ثلاثي

يتم تقديم مفهوم التكامل الثلاثي عن طريق القياس بتكامل مزدوج.

دعونا نحدد بعض المجال V في الفضاء المحاط بسطح مغلق S. دعونا نحدد دالة متصلة f (x ، y ، z) في هذا المجال المغلق. ثم نقسم المنطقة V إلى أجزاء عشوائية Δv i ، بافتراض أن حجم كل جزء يساوي Δv i ، ونؤلف مجموعًا كاملاً من النموذج

, (4)

الحد عند

المبالغ المتكاملة (11) ، التي لا تعتمد على طريقة تقسيم المجال V واختيار النقاط P i في كل مجال فرعي لهذا المجال ، تسمى التكامل الثلاثي للوظيفة f (x ، y ، z) على المجال الخامس:

. (5)

التكامل الثلاثي للدالة f (x ، y ، z) على المنطقة V يساوي التكامل الثلاثي على نفس المنطقة:

. (6)

1.3 تكاملات متعددة في إحداثيات منحنية الخطوط

دعونا نقدم إحداثيات منحنية الخطوط على المستوى تسمى الإحداثيات القطبية. دعنا نختار النقطة O (القطب) والشعاع الخارج منها (المحور القطبي).

أرز. الصورة 2 3

ستكون إحداثيات النقطة M (الشكل 2) هي طول مقطع MO - نصف القطر القطبي ρ والزاوية φ بين MO والمحور القطبي: M (ρ ، φ). لاحظ أنه بالنسبة لجميع نقاط المستوى ، باستثناء القطب ، ρ> 0 ، والزاوية القطبية φ ستُعتبر موجبة عند القياس في اتجاه عكس عقارب الساعة وسالب عند القياس في الاتجاه المعاكس.

يمكن تعيين العلاقة بين الإحداثيات القطبية والديكارتي للنقطة M من خلال محاذاة أصل نظام الإحداثيات الديكارتية مع القطب ، والمحور شبه الموجب - مع المحور القطبي (الشكل 3). ثم x = ρcosφ ، у = sinφ. من هنا

، tg.

في المجال D يحده المنحنيات ρ = Φ 1 (φ) و ρ = Φ 2 (φ) ، حيث φ 1< φ < φ 2 , непрерывную функцию z = f(φ, ρ) (рис. 4).

(7)

في الفضاء ثلاثي الأبعاد ، يتم إدخال إحداثيات أسطوانية وكروية.

الإحداثيات الأسطوانية للنقطة P (، φ، z) هي الإحداثيات القطبية ρ، لإسقاط هذه النقطة على مستوى Oxy وتطبيق هذه النقطة z (الشكل 5).

الشكل 5 الشكل 6

يمكن تحديد صيغ الانتقال من الإحداثيات الأسطوانية إلى الإحداثيات الديكارتية على النحو التالي:

x = ρcosφ ، y = sinφ ، z = z. (ثمانية)

في الإحداثيات الكروية ، يتم تحديد موضع نقطة في الفضاء بواسطة الإحداثيات الخطية r - المسافة من النقطة إلى أصل نظام الإحداثيات الديكارتية (أو قطب النظام الكروي) ، φ - الزاوية القطبية بين الموجب Oxyxis وإسقاط النقطة على المستوى Oxy و θ - الزاوية بين شبه المحور الموجب للمحور Оz والجزء OP (الشكل 6). حيث

دعونا نحدد صيغ الانتقال من الإحداثيات الكروية إلى الإحداثيات الديكارتية:

x = rsinθcosφ ، y = rsinθsinφ ، z = rcosθ. (تسع)

ثم ستبدو الصيغ الخاصة بالانتقال إلى إحداثيات أسطوانية أو كروية في التكامل الثلاثي كما يلي: